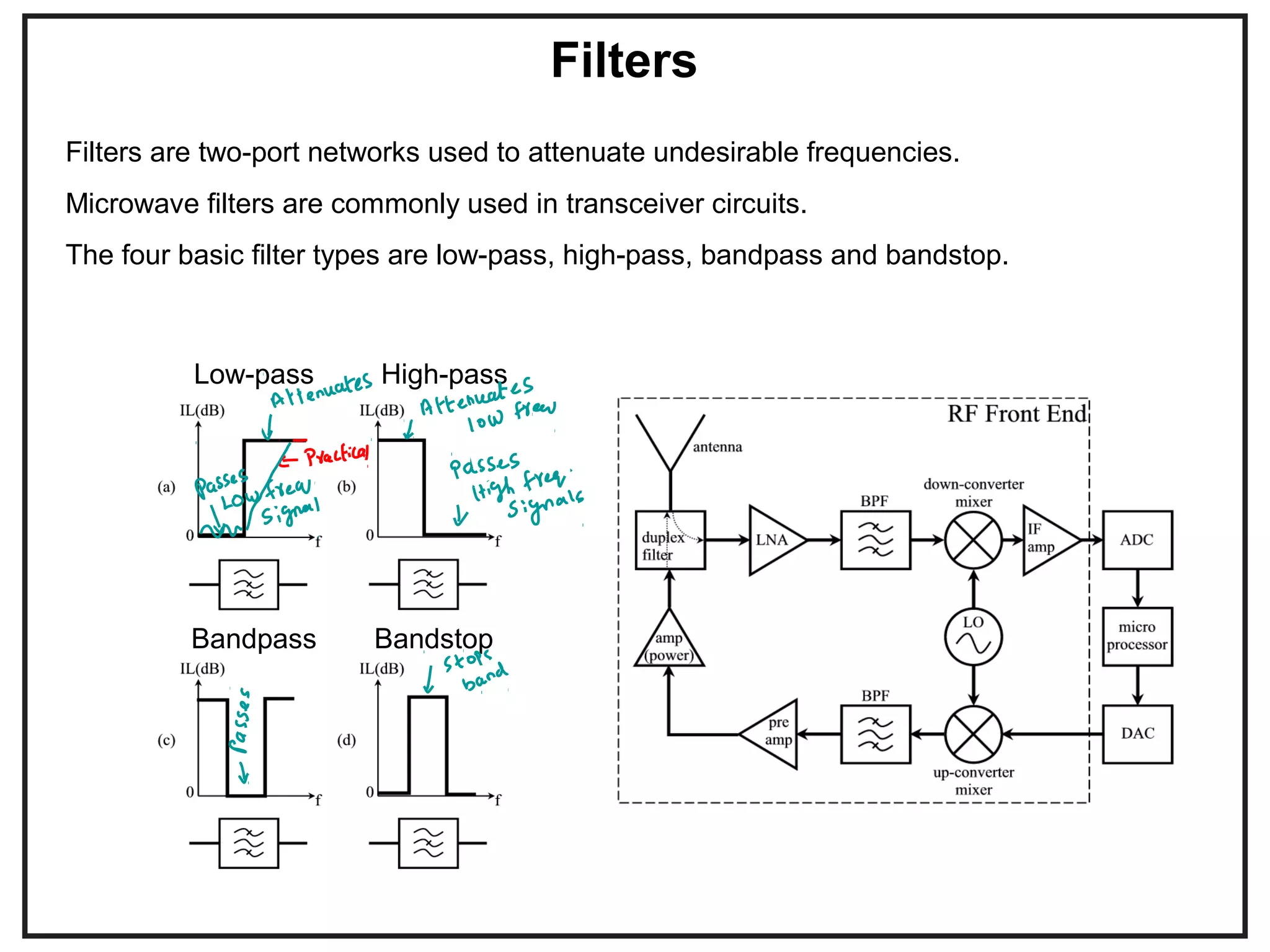
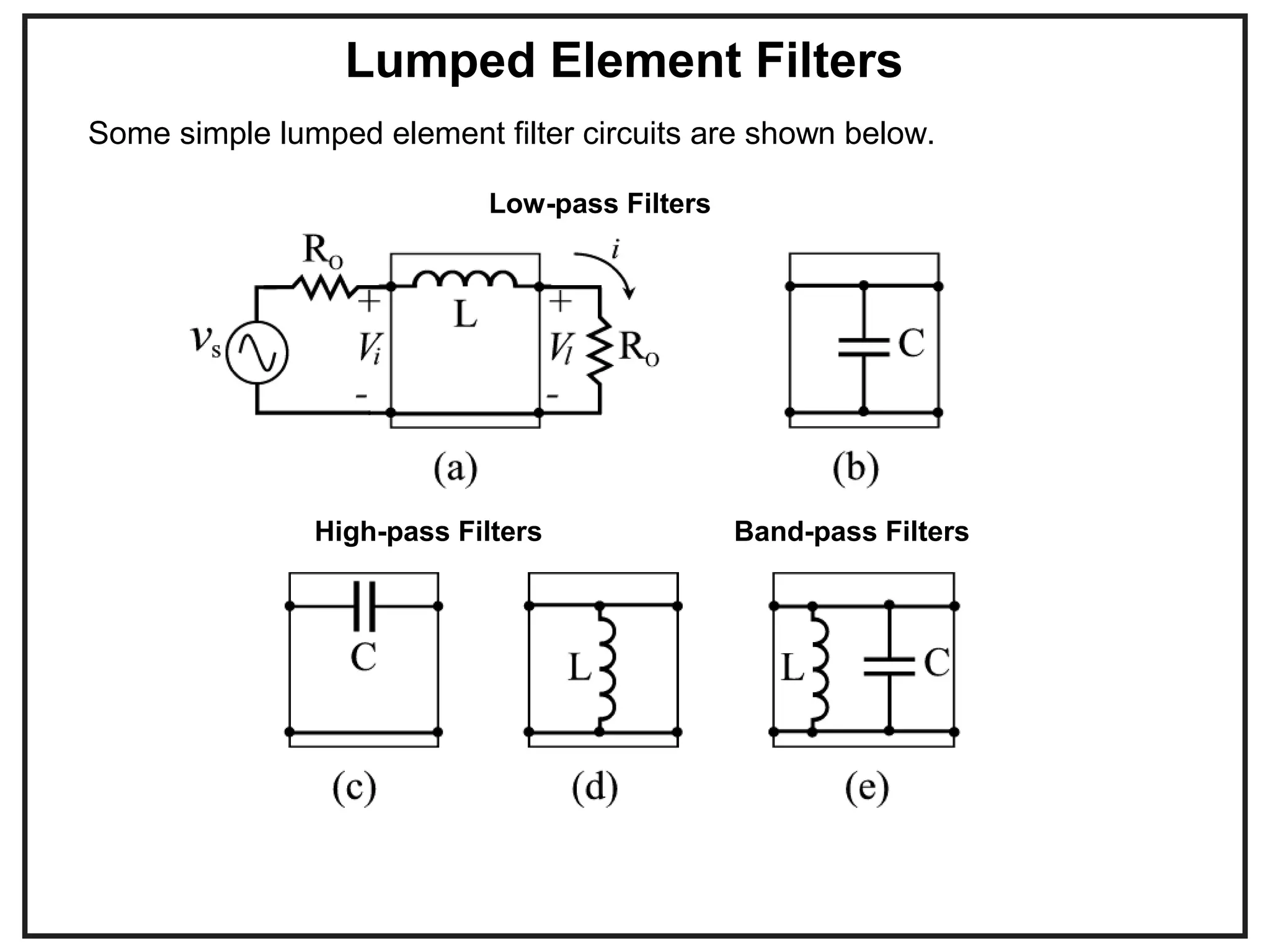
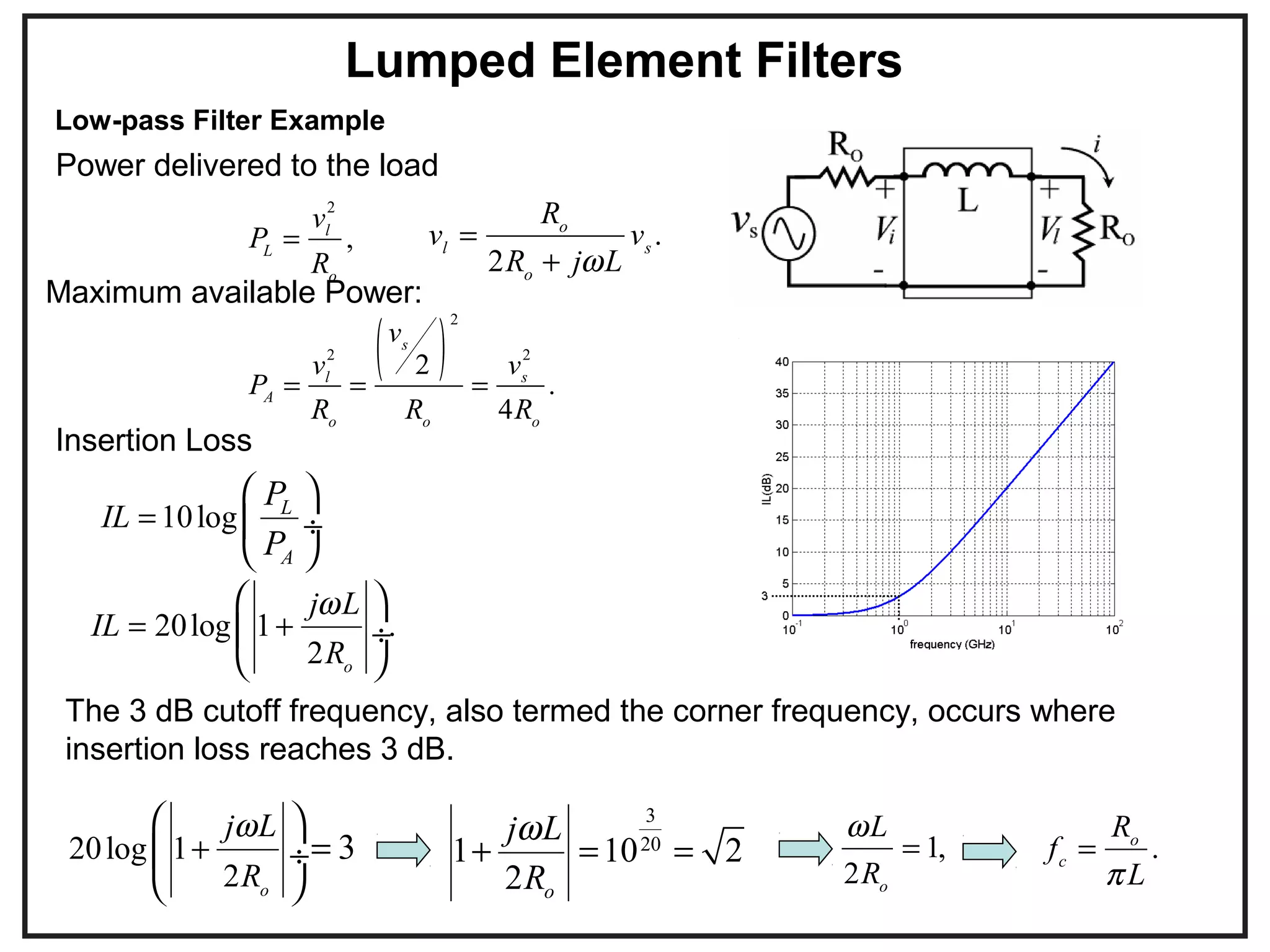
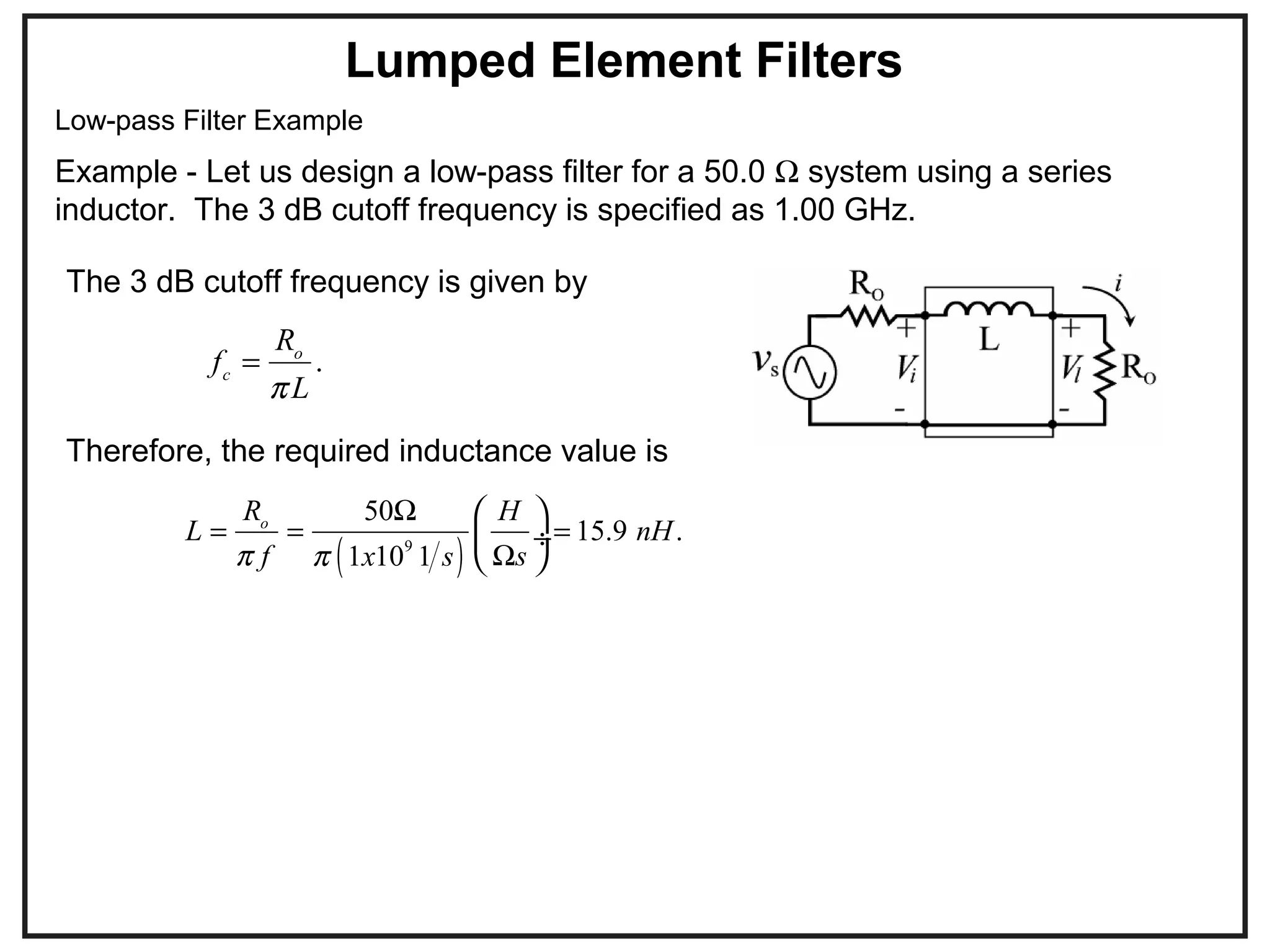
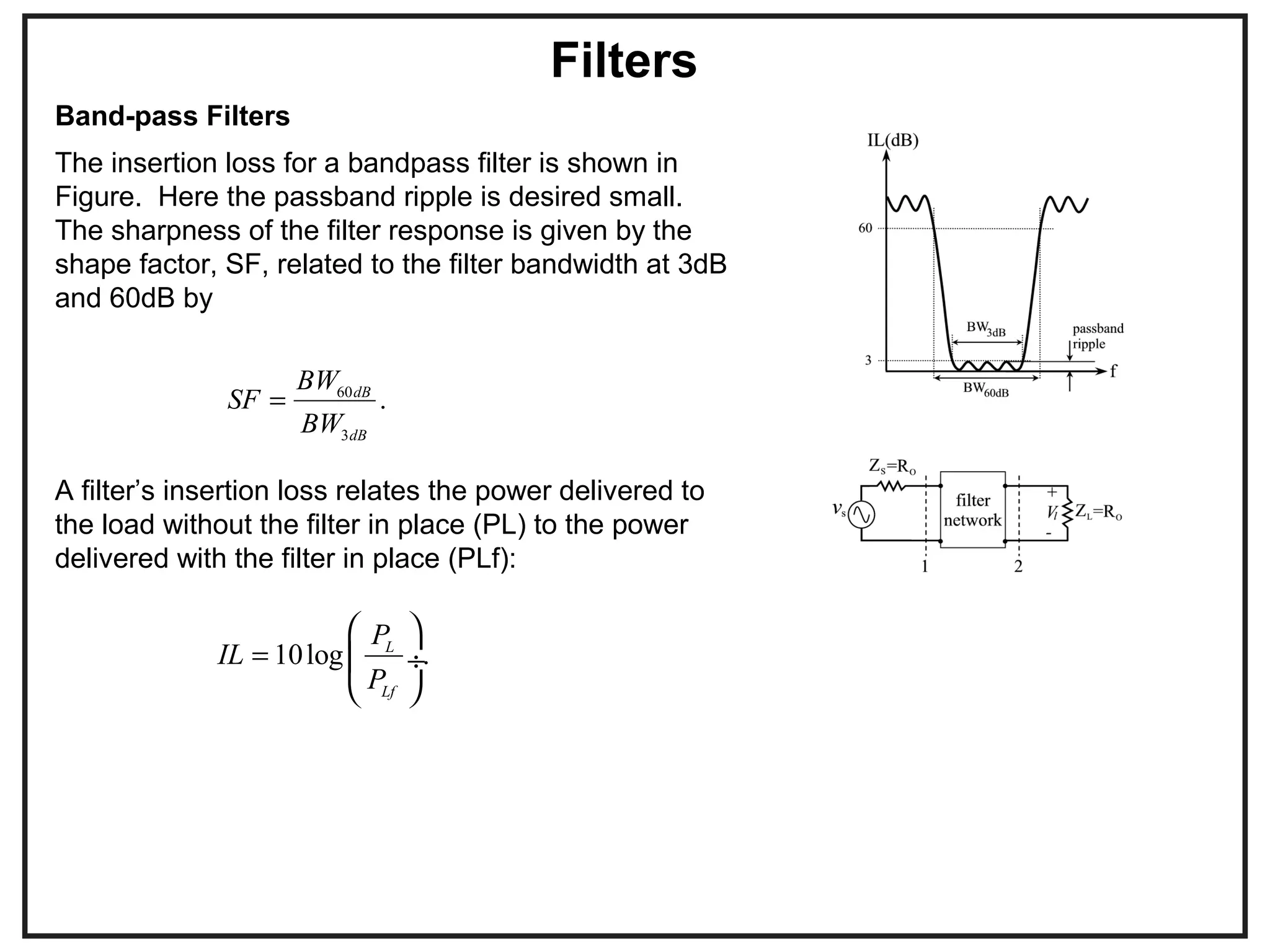
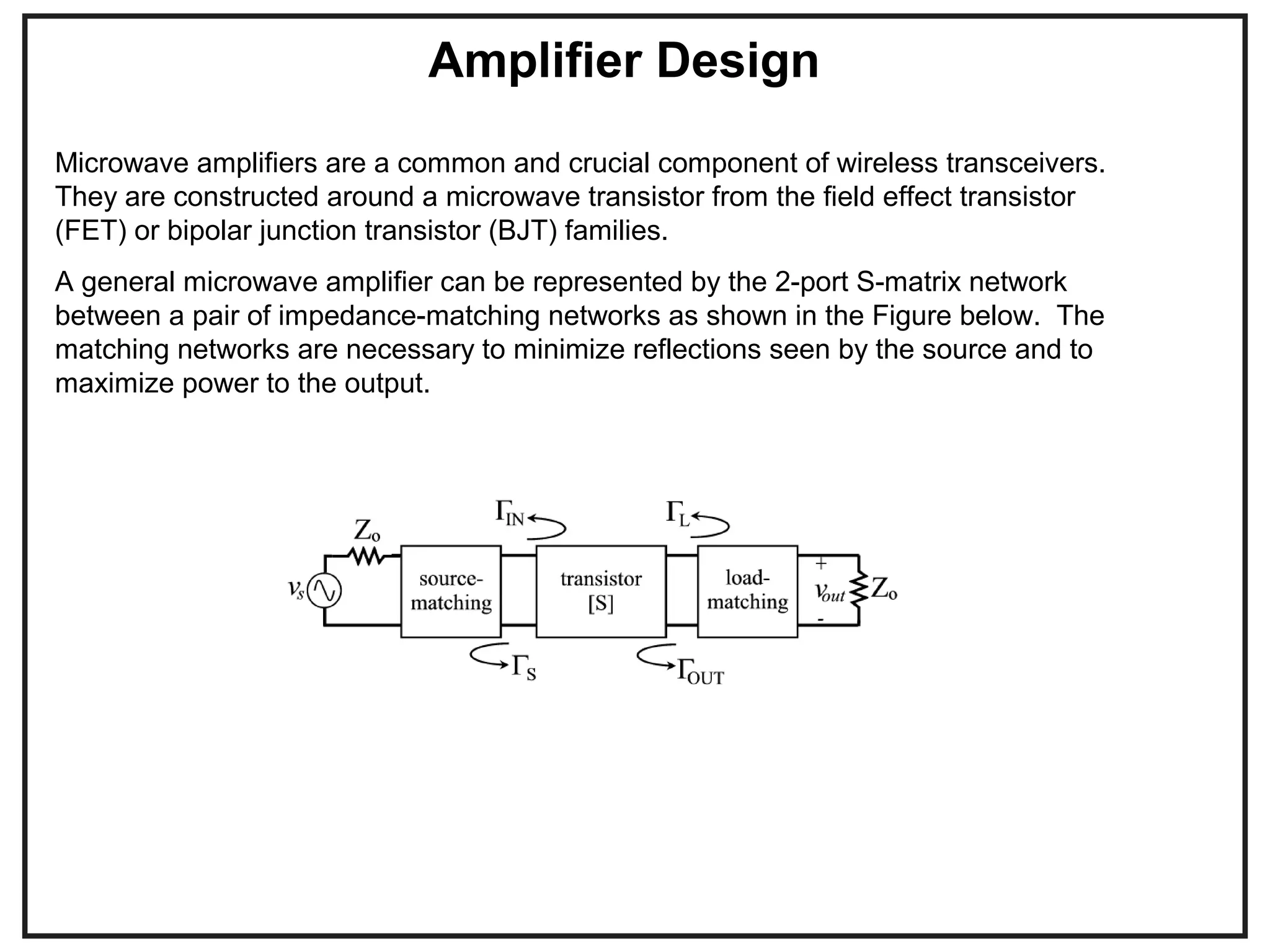
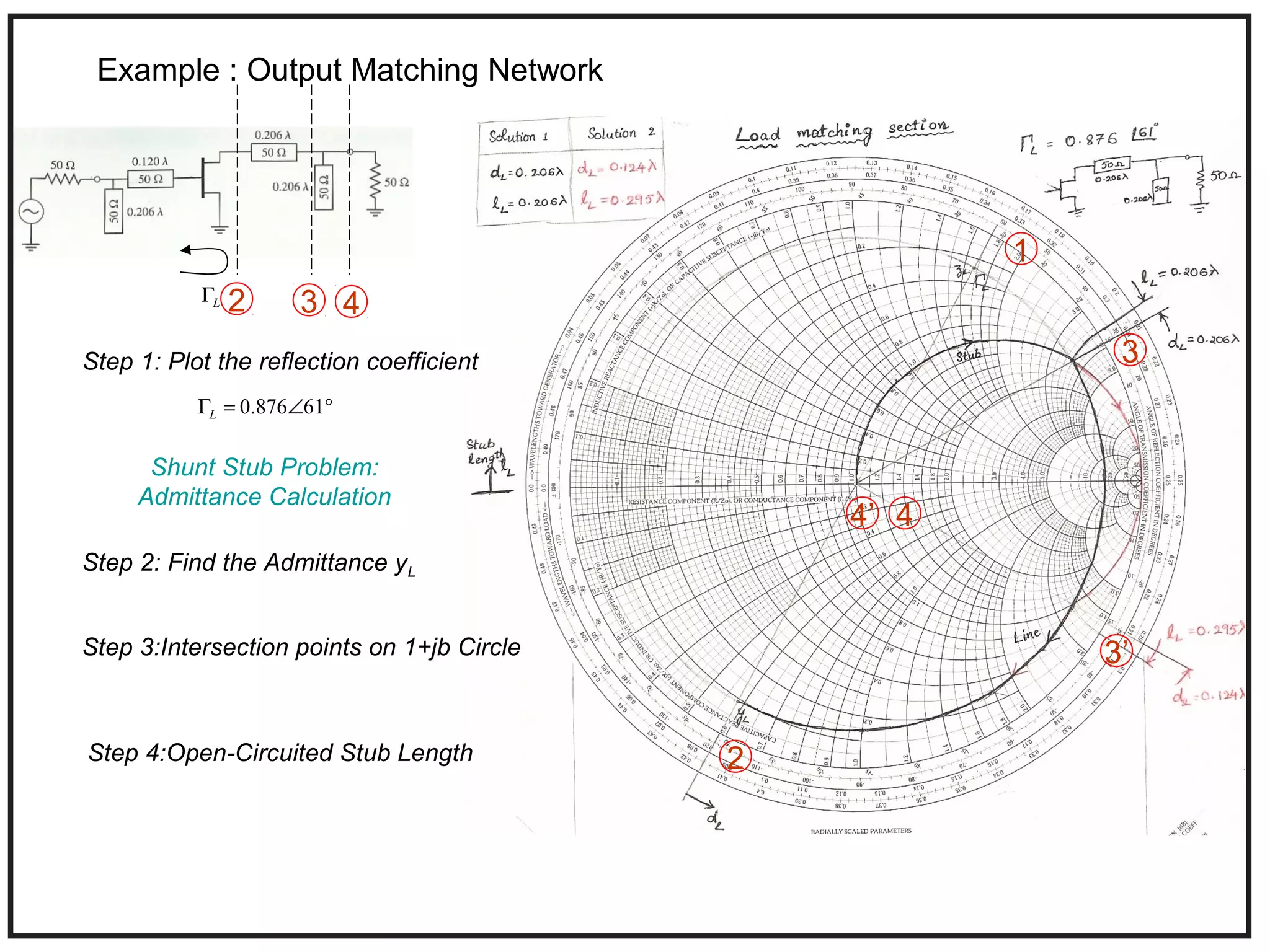
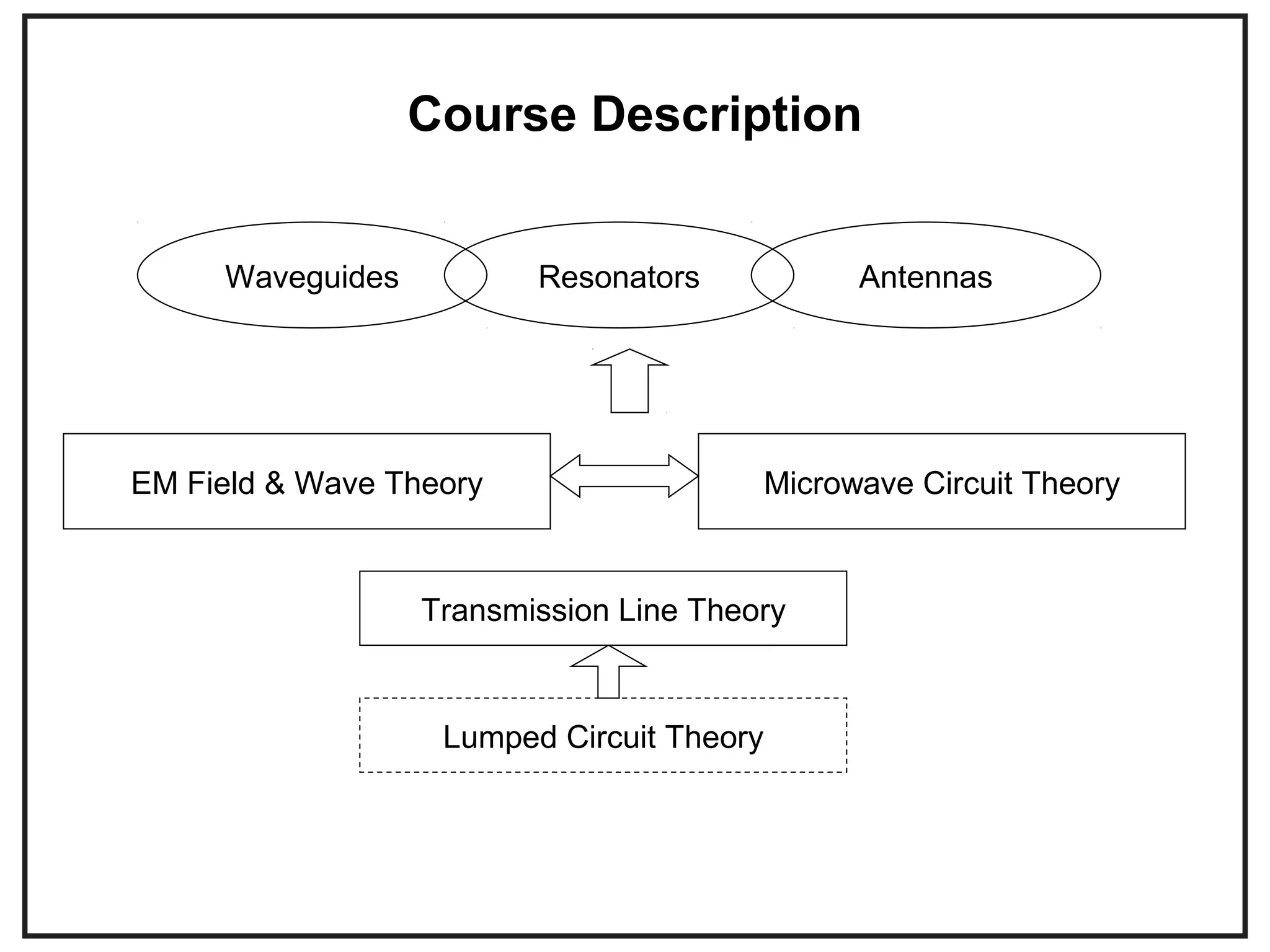
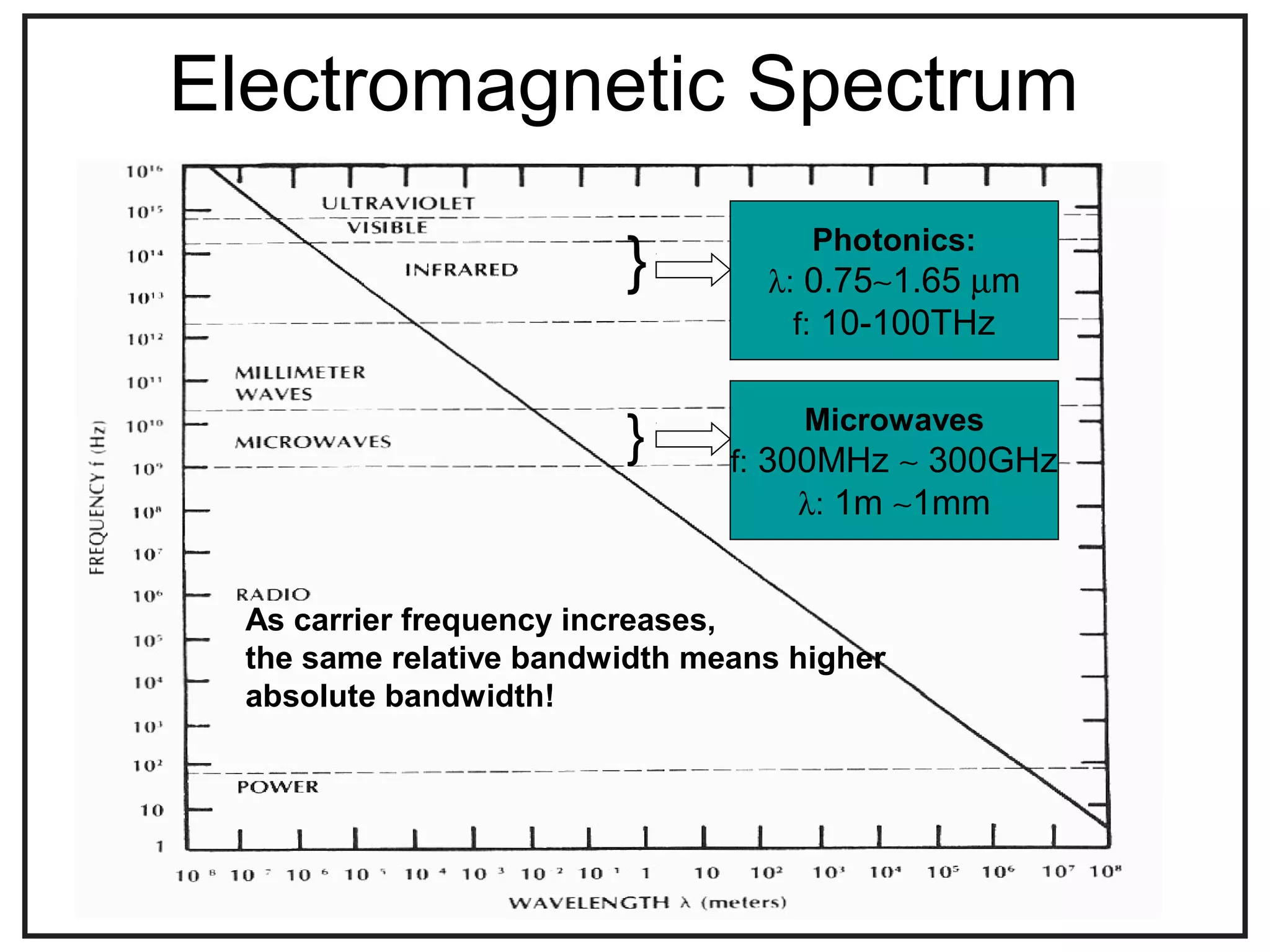
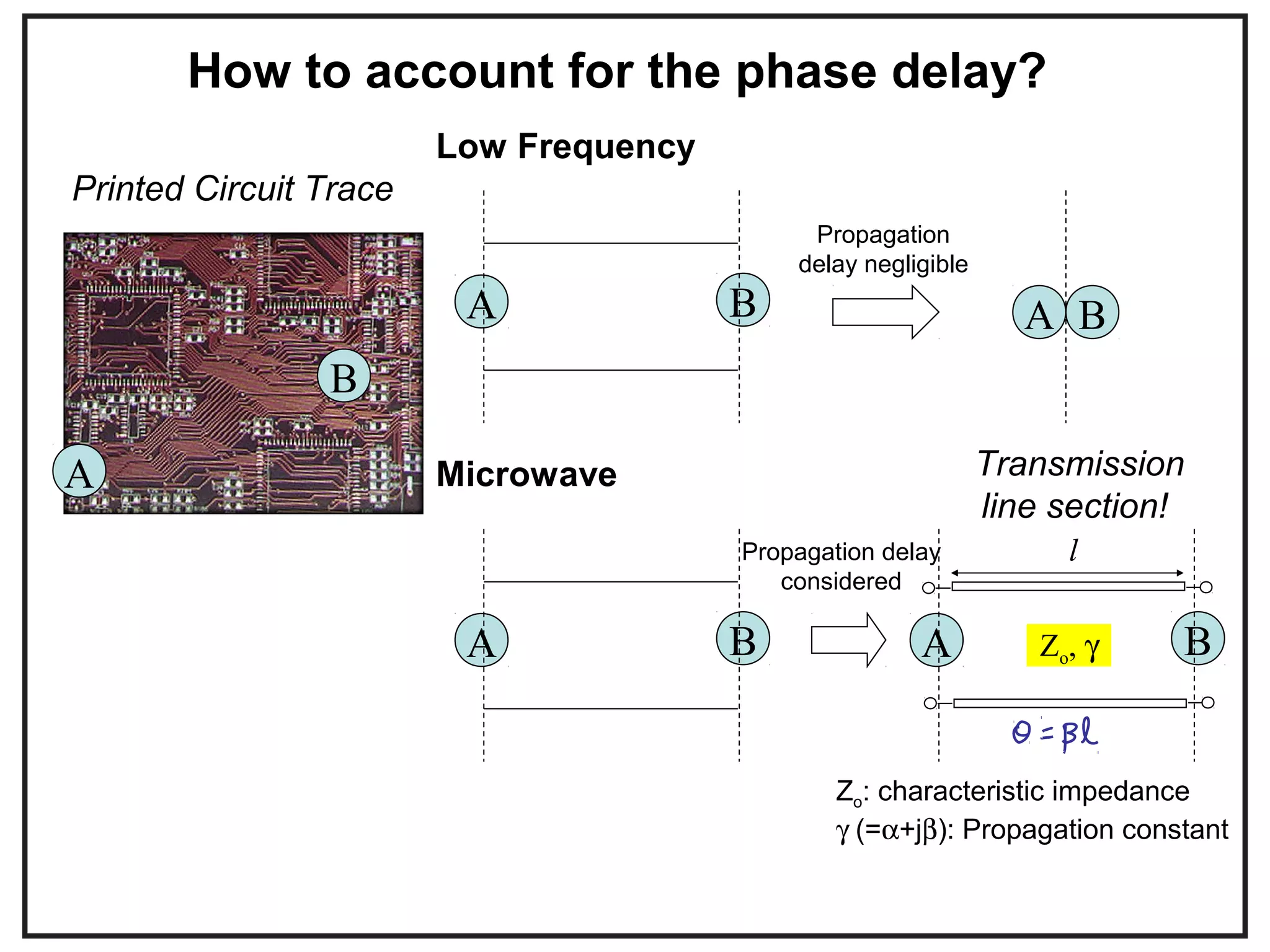
This document provides an overview of microwave engineering and describes key concepts such as transmission lines, scattering parameters, couplers, and filters. The objectives are to provide the basic theory of microwaves and examine applications in modern communication systems. Microwave engineering involves the design of systems like radar, satellite communications, and wireless networks that operate in the microwave frequency range from 300 MHz to 300 GHz.

1. Microwave Engineering
Prof. Tapas Mondal
Associate Professor
Department Of Electronics and Communication Engineering
West Bengal, India
Dr B C Roy Engineering College, Durgapur

2. Objectives
• To provide the basic theory pertaining to microwaves and other high-
frequency devices and subsystems.
• To examine some of its applications to modern communication
systems

3. Motivations
• Practical Reasons:
– Useful
– Fundamental
– Increasing important
• Intellectual Reasons
– Rigorous
– Elegant
– Challenging
• Energy/power generation &
transmission
• Telecommunications
• Other emerging applications
• Laws of EM waves have certain
beauty about them that can be
appreciated by those who
understand them on an aesthetic
level.

4. Course Description
Transmission Line Theory
EM Field & Wave Theory
Lumped Circuit Theory
Microwave Circuit Theory
Waveguides Resonators Antennas

5. Introduction to Microwaves
• Microwave Networks
– What are Microwaves?
– S-parameters
– Power Dividers
– Couplers
– Filters
– Amplifiers

6. Electromagnetic Spectrum
Photonics:
λ: 0.75∼1.65 µm
f: 10-100THz
}
Microwaves
f: 300MHz ∼ 300GHz
λ: 1m ∼1mm
}
As carrier frequency increases,
the same relative bandwidth means higher
absolute bandwidth!

7. Microwave engineering: Engineering and design of
communication/navigation systems in the microwave
frequency range.
Microwave Engineering
Applications: Microwave oven, Radar, Satellite,
communication, direct broadcast satellite (DBS) television,
personal communication systems (PCSs) etc.

8. What are Microwaves?
λ = 30 cm: f = 3 x 108
/ 30 x 10-2
= 1 GHz
λ = 1 cm: f = 3 x 108
/ 1x 10-2
= 30 GHz
Microwaves: 30 cm – 1 cm
Millimeter waves: 10 mm – 1 mm
(centimeter waves)
λ = 10 mm: f = 3 x 108
/ 10 x 10-3
= 30 GHz
λ = 1 mm: f = 3 x 108
/ 1x 10-3
= 300 GHz
( ) ( )
( )m
sm
Hz
/103
wavelength
clightofvelocity
ffrequency
8
λλ
×
==
Note: 1 Giga = 109

9. What are Microwaves?
f =10 kHz, λ = c/f = 3 x 108
/ 10 x 103
= 3000 m
Phase delay = (2π or 360°) x Physical length/Wavelength
f =10 GHz, λ = 3 x 108
/ 10 x 109
= 3 cm
Electrical length =1 cm/3000 m = 3.3 x 10-6
λ, Phase delay = 0.0012°
RF
Microwave
Electrical length = 0.33 λ, Phase delay = 118.8° !!!
1λ ≡ 360 °
Electrically long - The phase of a voltage or current changes
significantly over the physical extent of the device
Electrical length = Physical length/Wavelength (expressed in λ)

10. How to account for the phase delay?
A
B
A B A B
Low Frequency
Microwave
A B A B
Propagation
delay negligible
Transmission
line section!
l
Printed Circuit Trace
Zo: characteristic impedance
γ (=α+jβ): Propagation constant
Zo, γ
Propagation delay
considered

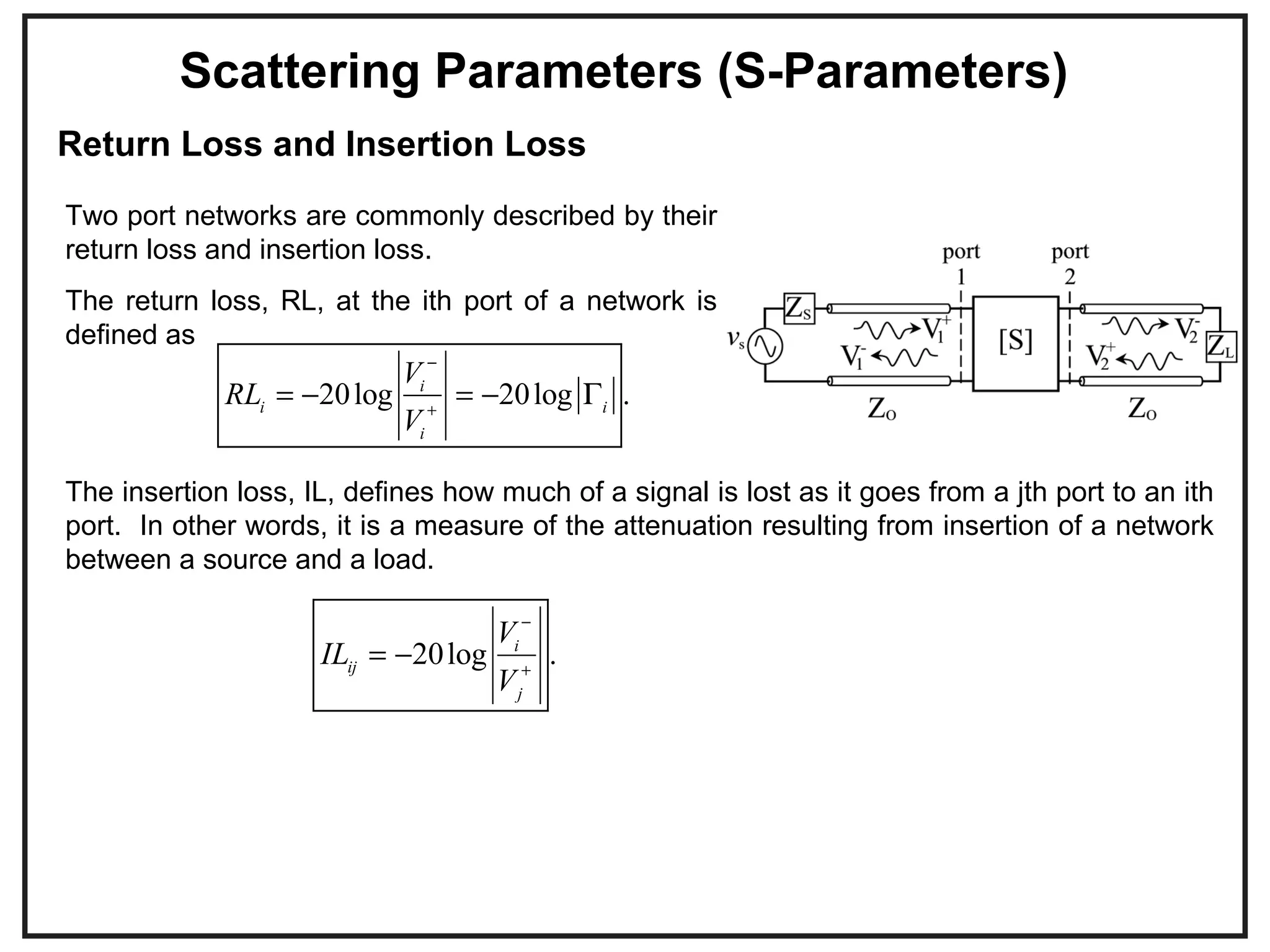
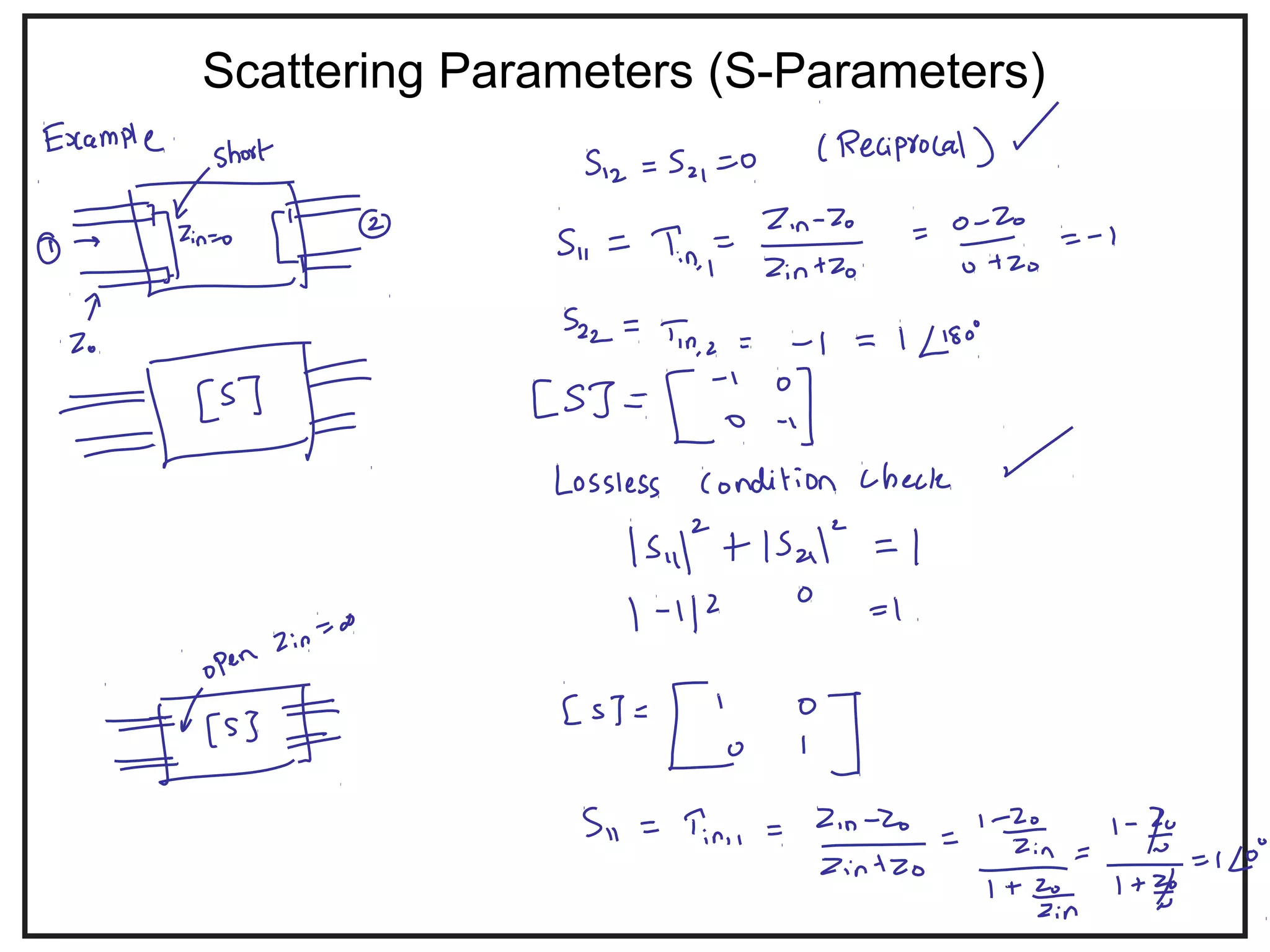
11. Scattering Parameters (S-Parameters)
•Consider a circuit or device inserted into a T-
Line as shown in the Figure.
•We can refer to this circuit or device as a
two-port network.
•The behavior of the network can be
completely characterized by its scattering
parameters (S-parameters), or its scattering
matrix, [S].
•Scattering matrices are frequently used to
characterize multiport networks, especially at
high frequencies.
•They are used to represent microwave
devices, such as amplifiers and circulators,
and are easily related to concepts of gain,
loss and reflection.
[ ] 11 12
21 22
S S
S
S S
 
=  
 
Scattering matrix

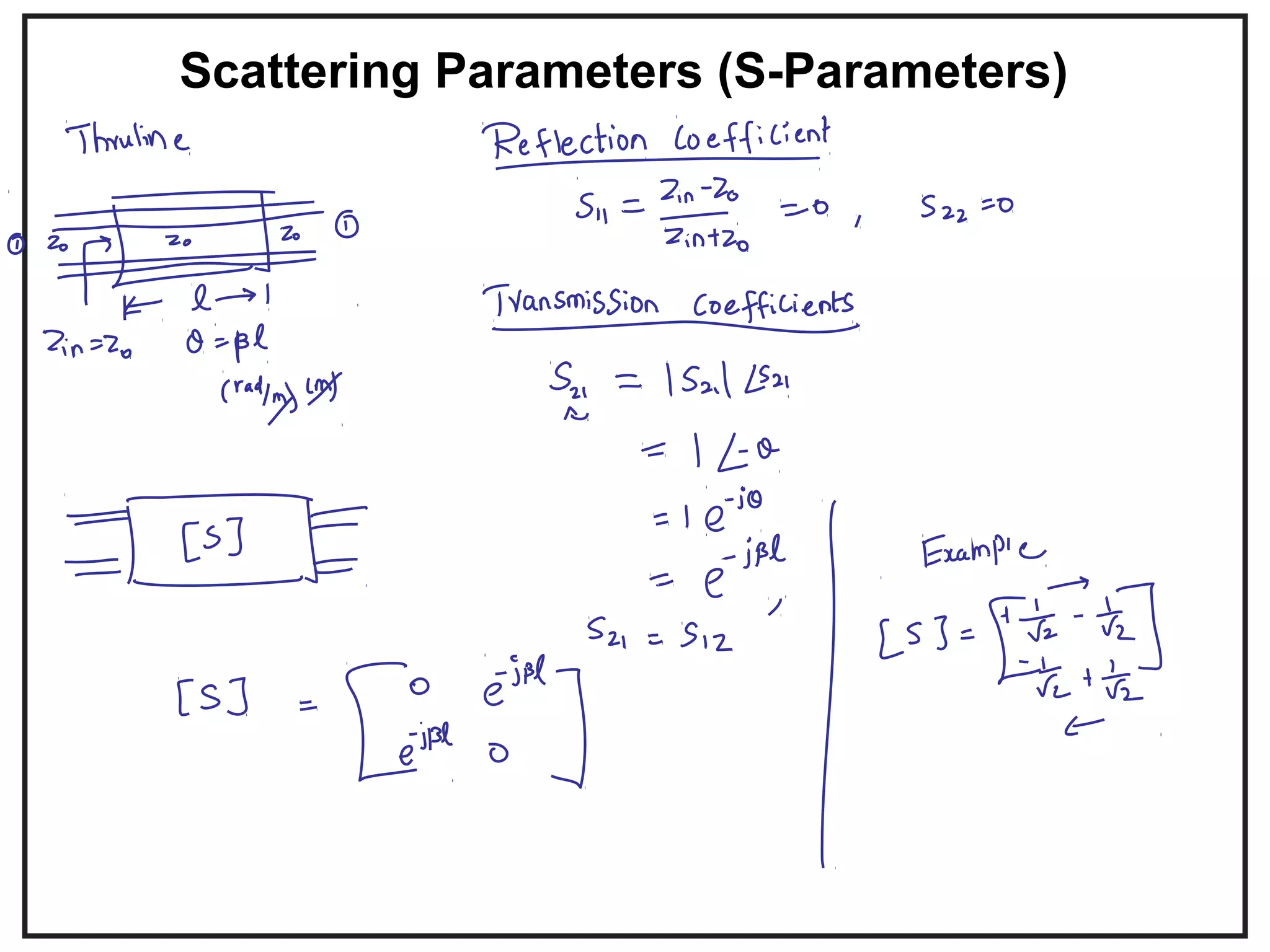
12. Scattering Parameters (S-Parameters)
The scattering parameters represent ratios of
voltage waves entering and leaving the ports
(If the same characteristic impedance, Zo, at
all ports in the network are the same).
1 11 1 12 2 .V S V S V− + +
= +
2 21 1 22 2
.V S V S V− + +
= +
11 121 1
21 222 2
,
S SV V
S SV V
− +
− +
=
    
    
    
In matrix form this is written
[ ] [ ][ ] .V S V
− +
=
2
1
11
1 0V
V
S
V +
−
+
=
=
1
1
12
2 0V
V
S
V +
−
+
=
=
1
2
22
2 0V
V
S
V +
−
+
=
=
2
2
21
1 0V
V
S
V +
−
+
=
=

13. Scattering Parameters (S-Parameters)
Properties:
The two-port network is reciprocal if the
transmission characteristics are the same in
both directions (i.e. S21 = S12).
It is a property of passive circuits (circuits with
no active devices or ferrites) that they form
reciprocal networks.
A network is reciprocal if it is equal to its
transpose. Stated mathematically, for a
reciprocal network
[ ] [ ] ,
t
S S=
11 12 11 21
21 22 12 22
.
t
S S S S
S S S S
=
   
   
   
12 21S S=Condition for Reciprocity:
1) Reciprocity

14. Scattering Parameters (S-Parameters)
Properties:
A lossless network does not contain any resistive
elements and there is no attenuation of the signal.
No real power is delivered to the network.
Consequently, for any passive lossless network,
what goes in must come out!
In terms of scattering parameters, a network is
lossless if
2) Lossless Networks
[ ] [ ] [ ]*
,
t
S S U=
1 0
[ ] .
0 1
U =
 
 
 
where [U] is the unitary matrix
For a 2-port network, the product of the transpose matrix and the complex conjugate
matrix yields
[ ] [ ]
( ) ( )
( ) ( )
2 2 * *
11 21 11 12 21 22*
2 2* *
12 11 22 21 12 22
1 0
0 1
t
S S S S S S
S S
S S S S S S
+ +
=
+ +
 
   =     
 
2 2
11 21
1S S+ =
If the network is reciprocal and lossless
* *
11 12 21 22
0S S S S+ =

15. Scattering Parameters (S-Parameters)
Return Loss and Insertion Loss
Two port networks are commonly described by their
return loss and insertion loss.
The return loss, RL, at the ith port of a network is
defined as
20log 20log .i
i i
i
V
RL
V
−
+
= − = − Γ
The insertion loss, IL, defines how much of a signal is lost as it goes from a jth port to an ith
port. In other words, it is a measure of the attenuation resulting from insertion of a network
between a source and a load.
20log .i
ij
j
V
IL
V
−
+
= −

16. Scattering Parameters (S-Parameters)

17. Scattering Parameters (S-Parameters)

18. Microwave Integrated Circuits
Microwave Integrated Circuits (MIC):
•Traces: transmission lines,
•Passive components: resistors, capacitors, and inductors
•Active devices: diodes and transistors.
Substrate Teflon fiber, alumina, quartz etc.
Metal Copper, Gold etc.
Process Conventional printed circuit
(Photolithography and etching)
Components Soldering and wire bonding

19. Lossless T-junction Power Divider
T-junction(Losslessdivider)
PD1.1
021
111
ZZZ
jBYin =++=
InputMatchingCondition
0=B
021
111
ZZZ
=+
o
o
in
Z
V
P
2
2
1
=
1
2
1
2
1
Z
V
P o
=
2
2
2
2
1
Z
V
P o
=
InputPower OutputPower
inPP
3
1
1 =
inPP
3
2
2 =
Ω= 50oZ
Ω== 15031 oZZ
Ω== 75
2
3
2 oZZ
Ω== 50|| 21 ZZZin
PowerDivider
EXAMPLE7.1
2:1
InputPortismatched
InputImpedance
Ingoringthejunction
reactance
Ω== 30|| 21 ZZZ oin Ω== 5.37|| 12 ZZZ oin
0=
+
−
=Γ
oin
oin
ZZ
ZZ
OutputPortsarenotmatched
InputPort OutputPort1 OutputPort2
Reflection
Coefficient 333.0
22
22
2 −=
+
−
=Γ
ZZ
ZZ
in
in
666.0
11
11
1 −=
+
−
=Γ
ZZ
ZZ
in
in
Power Divider
A T-junction power divider consists of
one input port and two output ports.
Design Example

20. [ ]












−
−
=
00
00
00
00
αβ
αβ
βα
βα
S
[ ]












=
0
0
0
0
342414
342313
242312
141312
SSS
SSS
SSS
SSS
S
[ ]












=
00
00
00
00
αβ
αβ
βα
βα
j
j
j
j
S
SymmetricCoupler AntisymmetricCoupler
122
=+βα
Areciprocal,lossless,matchedfour-portnetwork
behavesasadirectionalcoupler
Couplers
COUPLERS
A coupler will transmit half or more of its
power from its input (port 1) to its through
port (port 2).
A portion of the power will be drawn off to
the coupled port (port 3), and ideally none
will go to the isolated port (port 4).
If the isolated port is internally terminated
in a matched load, the coupler is most
often referred to as a directional coupler.
For a lossless network:
Coupling coefficient: ( )3120log .C S= −
( )2120log .IL S= −Insertion Loss:
( )4120log ,I S= −Isolation:
31
41
20log ,
S
D
S
=
 
 ÷
 
Directivity:
(dB)D I C= −

21. COUPLERS
Design Example
Example 10.10: Suppose an antisymmetrical coupler has the following characteristics:
C = 10.0 dB
D = 15.0 dB
IL = 2.00 dB
VSWR = 1.30
Coupling coefficient: ( )3120log .C S= −
( )2120log .IL S= −Insertion Loss:
10/ 20
31 10 0.316.S −
= =
2 / 20
21 10 0.794.S −
= =
11
1
0.130.
1
VSWR
S
VSWR
−
= =
+
25 ,I D C dB= + =
25/ 20
41 10 0.056.S −
= =
VSWR = 1.30
[ ]
0.130 0.794 0.316 0.056
0.794 0.130 0.056 0.316
0.316 0.056 0.130 0.794
0.056 0.316 0.794 0.130
S
−
=
−
 
 
 
 
 
 
Given

22. COUPLERS
[ ]
0 1 1 0
1 0 0 1
.
1 0 0 12
0 1 1 0
j
S
−−
=
−
 
 
 
 
 
 
[ ]
0 1 0
0 0 11
1 0 02
0 1 0
,
j
j
S
j
j
−
=
 
 
 
 
 
 
The quadrature hybrid (or branch-line hybrid) is
a 3 dB coupler. The quadrature term comes
from the 90 deg phase difference between the
outputs at ports 2 and 3.
The coupling and insertion loss are both equal
to 3 dB.
Ring hybrid (or rat-race) couplerQuadrature hybrid Coupler
A microwave signal fed at port 1 will split evenly
in both directions, giving identical signals out of
ports 2 and 3. But the split signals are 180 deg
out of phase at port 4, the isolated port, so they
cancel and no power exits port 4.
The insertion loss and coupling are both equal to
3 dB. Not only can the ring hybrid split power to
two ports, but it can add and subtract a pair of
signals.

23. Filters
Filters are two-port networks used to attenuate undesirable frequencies.
Microwave filters are commonly used in transceiver circuits.
The four basic filter types are low-pass, high-pass, bandpass and bandstop.
Low-pass High-pass
BandstopBandpass

24. A low-pass filter is characterized by the insertion loss
versus frequency plot in Figure.
Notice that there may be ripple in the pass band (the
frequency range desired to pass through the filter), and a
roll off in transmission above the cutoff or corner frequency,
fc.
Simple filters (like series inductors or shunt capacitors)
feature 20 dB/decade roll off. Sharper roll off is available
using active filters or multi section filters.
Active filters employ operational amplifiers that are limited
by performance to the lower RF frequencies. Multi section
filters use passive components (inductors and capacitors),
to achieve filtering.
The two primary types are the Butterworth and the
Chebyshev. A Butterworth filter has no ripple in the
passband, while the Chebyshev filter features sharper roll
off.
Filters
Low-pass Filters

25. Low-pass Filters
High-pass Filters Band-pass Filters
Lumped Element Filters
Some simple lumped element filter circuits are shown below.

26. Low-pass Filter Example
Lumped Element Filters
2
,l
L
o
v
P
R
= .
2
o
l s
o
R
v v
R j Lω
=
+
20log 1 .
2 o
j L
IL
R
ω
= +
 
 ÷
 
The 3 dB cutoff frequency, also termed the corner frequency, occurs where
insertion loss reaches 3 dB.
1,
2 o
L
R
ω
=20log 1
2
3
o
j L
R
ω
+
 
= ÷
 
3
20
1 10 2
2 o
j L
R
ω
+ = = .o
c
R
f
Lπ
=
( )
2
2 2
2
.
4
s
l s
A
o o o
v
v v
P
R R R
= = =
10log L
A
IL
P
P
=
 
 ÷
 
Power delivered to the load
Insertion Loss
Maximum available Power:

27. Low-pass Filter Example
Example - Let us design a low-pass filter for a 50.0 Ω system using a series
inductor. The 3 dB cutoff frequency is specified as 1.00 GHz.
Lumped Element Filters
.o
c
R
f
Lπ
=
The 3 dB cutoff frequency is given by
( )9
50
15.9 .
1 10 1
o
R H
L nH
f sx sπ π
Ω
= = =
Ω
 
 ÷
 
Therefore, the required inductance value is

28. Filters
The insertion loss for a bandpass filter is shown in
Figure. Here the passband ripple is desired small.
The sharpness of the filter response is given by the
shape factor, SF, related to the filter bandwidth at 3dB
and 60dB by
60
3
.dB
dB
BW
SF
BW
=
A filter’s insertion loss relates the power delivered to
the load without the filter in place (PL) to the power
delivered with the filter in place (PLf):
10log .L
Lf
P
IL
P
=
 
 ÷
 
Band-pass Filters

29. Amplifier Design
Microwave amplifiers are a common and crucial component of wireless transceivers.
They are constructed around a microwave transistor from the field effect transistor
(FET) or bipolar junction transistor (BJT) families.
A general microwave amplifier can be represented by the 2-port S-matrix network
between a pair of impedance-matching networks as shown in the Figure below. The
matching networks are necessary to minimize reflections seen by the source and to
maximize power to the output.

30. Example : Output Matching Network
Step 1: Plot the reflection coefficient
Step 3:Intersection points on 1+jb Circle
Step 4:Open-Circuited Stub Length
Step 2: Find the Admittance yL
Shunt Stub Problem:
Admittance Calculation
°∠=Γ 61876.0L
LΓ
1
2
3
4
3’
4’
2 3 4

31. Example : Input Matching Network
Step 1: Plot the reflection coefficient
Step 3:Intersection points on 1+jb Circle
Step 4:Open-Circuited Stub Length
Step 2: Find the Admittance ys
1
2
3
4
Shunt Stub Problem:
Admittance Calculation
λ120.01 =d
5.311 jy +=
λ206.01 =
°∠=Γ 123872.0s
SΓ
X
Ignore
Treat as a load
234

32. References :
1. Microwave Engineering, third Edition ; David M. Pozar, Wiley Publications
Thank You…
Prof. Tapas Mondal