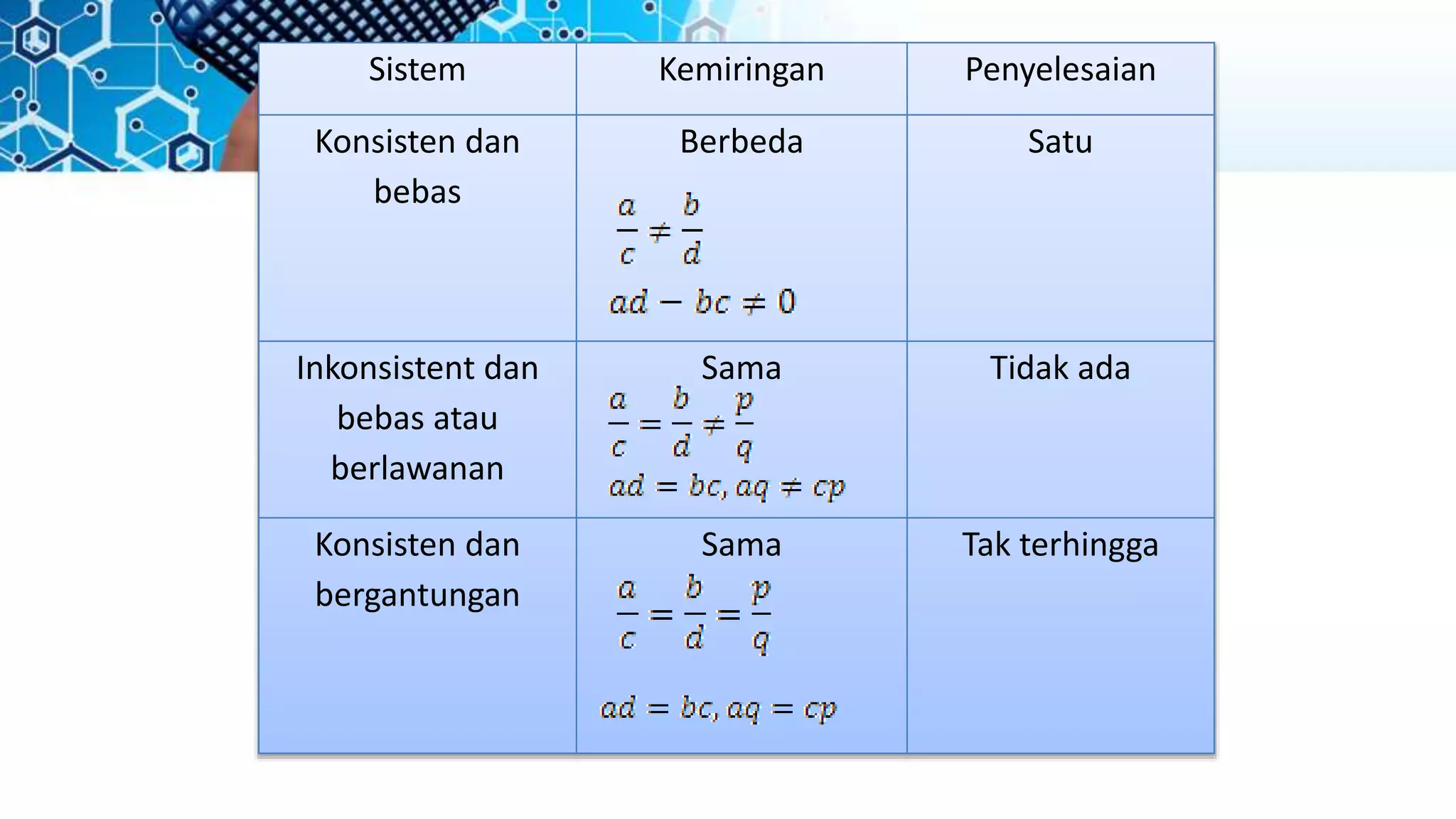
Dokumen ini menjelaskan tentang sistem persamaan linear, termasuk definisi, bentuk umum, dan metode penyelesaiannya, seperti metode grafik, substitusi, eliminasi, dan campuran. Setiap metode dijelaskan dengan langkah-langkah dan contoh, serta mencakup penggunaan determinan dalam penyelesaian. Berbagai hubungan dan kondisi sistem persamaan juga diulas untuk menggambarkan solusi yang mungkin ada.

1. FPPT.com
SISTEM PERSAMAAN
LINEAR

2. • Persamaan linear satu variabel adalah kalimat
terbuka yang menyatakan hubungan sama dengan
dan hanya memiliki satu variabel berpangkat satu.
Bentuk umum persamaan linear satu variabel adalah
ax + b = c, dengan a,b,c R dan a  0
•

3. • Persamaan linear dua variabel adalah persamaan
yang mengandung dua variabel dengan pangkat
masing-masing variabel sama dengan satu. Bentuk
umum persamaan linear dua variabel adalah
ax + by = c, dengan a,b,c R dan a  0, b  0

4. SISTEM PERSAMAAN LINEAR DUA VARIABEL
(SPLDV)
Pasangan dua persamaan linear dua veriabel (atau lebih)
yang ekuivalen dengan bentuk umum
dengan penyelesaian, simultan atau serentak terpenuhi
oleh pasangan terurut (x0, y0) dinamakan sistem
persamaan linear dua variabel (SPLDV)
Dengan a,b,c,d,p,q,
R
dan a,b,c,d ≠0

5. Metode Penyelesaian SPLDV
• Metode Grafik
• Metode Substitusi
• Metode Eliminasi
• Metode Eliminasi Substitusi

6. Metode Grafik
• Adalah metode penyelesaian SPLDV yang dilakukan
dengan cara menggambar grafik dari kedua
persamaan tersebut yang kemudian menentukan titik
potongnya.

7. Metode Grafik
 Perhatikan dua sistem persamaan dua
variabel
 Solusi dari sistem ini adalah himpunan
pasangan terurut yang merupakan solusi
dari kedua persamaan.
 Grafik garis menunjukkan himpunan
penyelesaian dari masing-masing
persamaan dalam sistem. Oleh karena itu,
perpotongan kedua garis adalah gambar
dari penyelesaian sistem.
 Solusi dari sistem adalah

8. Grafik mungkin sejajar atau mungkin berimpit.

9. Sistem Kemiringan Grafik Penyelesaian
Konsisten dan bebas Berbeda Garis
berpotongan di
satu titik
Satu
Inkonsistent dan bebas
atau berlawanan
Sama Garis sejajar Tidak ada
Konsisten dan
bergantungan
Sama Garis berimpit Tak terhingga
Hubungan yang mungkin diantara sebuah sistem, kemiringan dari masing masing
grafik, dan penyelesaian persamaan ditunjukkan pada table berikut.
Dengan a,b,c,d,p,q,
R
dan a,b,c,d ≠0

10. Metode Substitusi
Adalah metode penyelesaian SPLDV dengan cara
menggantikan satu variabel dengan variabel dari persamaan
yang lain
Langkah-langkah
1. Pilih salah satu persamaan yang paling sederhana
kemudian nyatakan x sebagai fungsi y atau y sebai
fungsi x
2. Substitusikan x atau y pada langkah 1 ke persamaan
yang lainnya

11. Contoh
• Tentukan himpunan Penyelesaian dari persamaan linier dengan metode substitusi
• 3x + 4y = 11 … pers.(1)
• x + 7y = 15 … pers. (2)
• Jawab :
• Dari pers.(2) didapat : x = 15 – 7y … pers.(3)
• Kmd substitusikan pers.(3) ke pers.(1) :
• 3x + 4y = 11 Harga y = 2 kmd
• ⇔ 3(15 – 7y) + 4y = 11 substitusikan ke pers(3) :
• ⇔ 45 – 21y + 4y = 11 x = 15 – 7y
• ⇔ - 21y + 4y = 11 – 45 x = 15 – 7(2)
• ⇔ - 17y = - 34 ⇔ x = 15 – 14
• x = 1
• Jd, HP = { 1, 2 }
2
17
34



y

12. b) Tentukan HP dari persamaan linear berikut dg metode substitusi !
2x + 3y = 1 … pers.(1)
3x + y = 5 … pers.(2)
Jawab :
Dari pers.(2) didapat : y = 5 – 3x … pers.(3). Harga x = 2 kmd
Kmd substitusikan pers.(3) ke pers.(1) : disubstitusikan ke pers.(3) :
2x + 3y = 1 y = 5 – 3x
2x + 3(5 – 3x) = 1 y = 5 – 3(2)
2x + 15 – 9x = 1 y = 5 – 6
2x – 9x = 1 – 15 y = - 1
- 7x = - 14
x = 2 Jd, HP = { 2, - 1}

13. Metode Eliminasi
 Adalah metode penyelesaian SPLDV dengan cara menghilangkan
salah satu variabel.
 Langkah-langkah
1. Perhatikan koefisien x (atau y)
a) Jika koefisiennya sama:
i. Lakukan operasi pengurangan untuk tanda yang sama
ii. Lakukan operasi penjumlahan untuk tanda yang berbeda
b) Jika koefisiennya berbeda, samakan koefisiennya dengan cara mengalikan
persamaan-persamaan dengan konstanta yang sesuai, lalu lakukan
seperti langkah a)
2. Lakukan kembali langkah 1 untuk mengeliminasi variabel lainnya.

14. Contoh Metode Eliminasi
Contoh : Mengeliminasi X
Tentukan Himpunan Penyelesaian (HP) dari persamaan linear berikut dg metode
eliminasi !
2x + 3y = 1 … pers.(1)
3x + y = 5 … pers.(2)
Jawab :
Mengeliminasi x
2x + 3y = 1 x3 6x + 9y = 3
3x + y = 5 x2 6x + 2y = 10 –
7y = - 7
y = -1

15. Mengeliminasi y
2x + 3y = 1 x1 2x + 3y = 1
3x + y = 5 x3 9x + 3y = 15 –
- 7x = - 14
x = 2
Jd, HP = { 2, -1 }
Catatan :
“ Jika kita mengeliminasi (menghilangkan) variabel x
maka yg akan kita dapatkan nantinya adlh nilai dari variabel y
dan sebaliknya, jika kita mengeliminasi variabel y maka yg
akan kita dapatkan nantinya adlh nilai dari variabel x “

16. Metode Eliminasi-Substitusi
• Adalah metode penyelesaian SPLDV dengan cara
menggabungkan metode eliminasi dan metode
substitusi.
• Metode eliminasi digunakan untuk mendapatkan
variabel pertama, dan hasilnya disubstitusikan ke
persamaan untuk mendapatkan variabel kedua

17. Penyelesaian Umum dari SPLDV
 Untuk semua bilangan real a,b,c,d,p,q , penyelesaian dari sistem
 Adalah
dan
Dengan, ad - bc  0

18. Sistem Kemiringan Penyelesaian
Konsisten dan
bebas
Berbeda Satu
Inkonsistent dan
bebas atau
berlawanan
Sama Tidak ada
Konsisten dan
bergantungan
Sama Tak terhingga

19. 3. Metode Campuran
Pada metode ini, merupakan gabungan dari cara eliminasi dan
substitusi.
Contoh :
a) Tentukan HP dari persamaan linear berikut dg metode campuran !
3x + 4y = 11 … pers.(1)
x + 7y = 15 … pers.(2)
Jawab :
3x + 4y = 11 x 1 3x + 4y = 11
x + 7y = 15 x 3 3x + 21y = 45 -
- 17y = - 34
⇔ y = 2
Harga y = 2 kmd substitusikan ke pers(2) :
x + 7y = 15
⇔ x + 7(2) = 15
⇔ x + 14 = 15
⇔ x = 15 – 14 ⇔ x = 1 Jd, HP = { 1, 2 }

20. 2x + 3y = 1 … pers.(1)
4x – 3y = 11 … pers.(2)
Jawab :
2x + 3y = 1
4x – 3y = 11 +
⇔ 6x = 12
⇔ x = 2
Harga x = 2 kmd substitusikan ke pers.(1) :
2x + 3y = 1
⇔ 2(2) + 3y = 1
⇔ 4 + 3y = 1
⇔ 3y = 1 – 4
⇔ 3y = - 3
⇔ y = - 1 Jd, HP = { 2, -1 }
b) Tentukan HP Dari Persamaan Linear Berikut Dg Metode
Campuran !

21. 4. Determinan
• Definisi:
Determinan adalah bilangan real yang direpresentasikan oleh susunan bilangan
yang berbentuk persegi.
• Definisi:
Nilai dari determinan orde dua

22. Aturan Cramer
 Untuk semua bilangan real a1, b1, c1, a2, b2 dan c2 , penyelesaian dari sistem
 Adalah
 Dengan, D ≠ 0
 Jika , D = 0 sistem tidak memiliki penyelesaian atau mempunyai penyelesaian banyak tak terhingga.

23. 4. Metode Determinan
Sistem persamaan, misalkan :
ax + by = c
px + qy = r
Menurut aturan determinan diubah mjd :
Artinya dan utk variabel x dan y
didefinisikan :
,

qp
ba
pbqa
qp
ba
.. 
pbqa
rbqcqr
bc
x
..
..





pbqa
pcrarp
ca
y
..
..






24. Contoh :
Tentukan HP dari SPL berikut !
4x – 5y = 22
7x + 3y = 15
Kita cari dl determinannya :
Jd, HP = { 3, -2}
3
47
141
47
7566
47
15)5(3.22315
522







x
4735127)5(3.4
37
54



2
47
94
47
15460
47
7.2215.4157
224








y

25. Contoh
• 2x + 3y = 1 dan 3x + y = 5
D =
2 3
3 1
= 2.1 – 3.3 = 2 – 9 = -7
Dx =
1 3
5 1
= 1.1 − 5.3 = 1 – 15 = -14
Dy =
2 1
3 5
= 2.5 − 3.1 = 10 − 3 = 7
• Sehingga diperoleh
• X = -14/-7 = 2 dan Y = 7/-7 = -1
• Jadi HP = ( 2, -1 )

26. Latihan
1. Diberikan suatu bilangan yang terdiri atas dua angka.
Empat kali angka satuan adalah kurang enam dari
dua kali angka puluhan. Bilangan itu adalah sembilan
kurang dari tiga kali bilangan yang dicari dengan
membalik angka-angkanya.
tentukan bilangan itu.

27. Latihan
2. Dua tahun yang lalu umur Harry 6 kali umur Laras.
Delapan belas tahun kemudian akan menjadi dua kali
umur Laras. Tentukan umur mereka masing-masing!

28. • SEKIAN DAN TERIMA KASIH
• WASSALAM