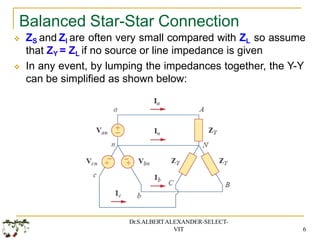
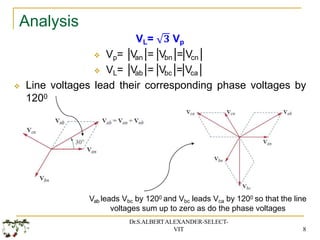
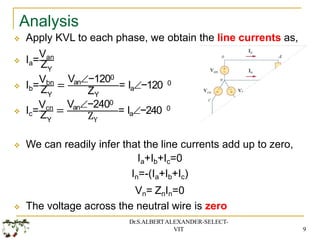
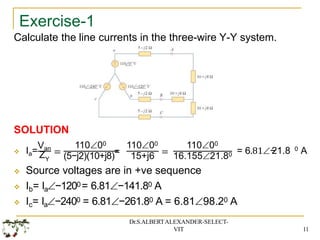
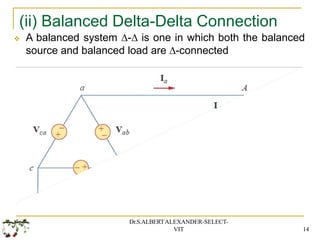
The document covers fundamental concepts in basic electrical and electronics engineering, primarily focusing on three-phase systems, alternating voltages and currents, and various connections including star and delta configurations. It elaborates on the characteristics of balanced loads in different connection types and provides mathematical analysis for calculating line and phase currents, power factors, and other related parameters. Additionally, it includes exercises with solutions to reinforce the theoretical aspects discussed.

1. BEEE102L BASIC ELECTRICAL
AND ELECTRONICS
ENGINEERING
Dr.S.ALBERT ALEXANDER
SCHOOL OF ELECTRICAL ENGINEERING
albert.alexander@vit.ac.in
1
Dr.S.ALBERTALEXANDER-
SELECT-VIT

2. Module 2
Dr.S.ALBERTALEXANDER-SELECT-
VIT 2
 Alternating voltages and currents
 RMS, average, maximum values
 Single Phase RL, RC, RLC series circuits
 Power in AC circuits
 Power Factor
 Three phase balanced systems
 Star and delta Connections
 Electrical Safety, Fuses and Earthing

3. 2.7 Star and Delta Connections
Dr.S.ALBERTALEXANDER-SELECT-
VIT 3
 Since both the 3 source and 3 load can be either wye- or
delta-connected, we have four possible connections: Y-Y,
Y-, - and -Y
 A balanced delta-connected load is more common than a
balanced wye-connected load
 It is due to the ease with which loads may be added or
removed from each phase of a delta-connected load
 It is very difficult with a wye-connected load because the
neutral may not be accessible
 On the other hand, delta-connected sources are not
common in practice because of the circulating current that
will result in the delta-mesh if the three-phase voltages are
slightly unbalanced

4. (i) Balanced Star-Star Connection
 A balanced Y-Y system is a three-phase system with a
balanced Y-connected source and a balanced Y-connected
load
 A Y-connected load is connected to a Y-connected source
Dr.S.ALBERTALEXANDER-SELECT-
VIT 4

5. Balanced Star-Star Connection
Dr.S.ALBERTALEXANDER-SELECT-
VIT 5
 Assume a balanced load so that load impedances are
equal
 Although the impedance ZY is the total load impedance per
phase, it may also be regarded as the sum of the source
impedance ZS, line impedance Zl and load impedance ZL
for each phase, since these impedances are in series
 ZS denotes the internal impedance of the phase winding of
the generator
 Zl is the impedance of the line joining a phase of the source
with a phase of the load
 ZL is the impedance of each phase of the load
 Zn is the impedance of the neutral line.
ZY = ZS +Zl +ZL

6. Balanced Star-Star Connection
 ZS and Zl are often very small compared with ZL so assume
that ZY = ZL if no source or line impedance is given
 In any event, by lumping the impedances together, the Y-Y
can be simplified as shown below:
Dr.S.ALBERTALEXANDER-SELECT-
VIT 6

7. Analysis
 Assuming the positive sequence, the phase voltages (or
line-to neutral voltages) are Van= Vp00; Vbn= Vp-1200 and
Vcn= Vp-2400
 The line-to-line voltages or simply line voltages Vab, Vbc
and Vca are related to the phase voltages
 Vab= Van+Vnb=Van-Vbn = Vp00 - Vp-1200
ab p 2 2 p
 V = V (1 + 1
+j 3
)= 3 V 300
 Similarly, Vbc= Vbn-Vcn = 3 Vp-900
 Vca= Vcn-Van = 3 Vp-2100
 Magnitude of the line voltages is times the magnitude of
the phase voltages Vp or VL= 𝟑 Vp
Dr.S.ALBERTALEXANDER-SELECT-
VIT 7

8. Analysis
VL= 𝟑 Vp
 Vp= │
V
an│=│
Vbn│
=│
Vcn│
 VL= │
V
ab│=│
Vbc│
=│
Vca│
 Line voltages lead their corresponding phase voltages by
1200
Vab leads Vbc by 1200 and Vbc leads Vca by 1200 so that the line
voltages sum up to zero as do the phase voltages
Dr.S.ALBERTALEXANDER-SELECT-
VIT 8

9. Analysis
 Apply KVL to each phase, we obtain the line currents as,
Van
 Ia= ZY
Vbn
 Ib= ZY
=
Van−1200
ZY
= Ia−120 0
Vcn
 Ic= Z =
Van−2400
Z
Y Y
= Ia−240 0
 We can readily infer that the line currents add up to zero,
Ia+Ib+Ic=0
In=-(Ia+Ib+Ic)
Vn= ZnIn=0
 The voltage across the neutral wire is zero
Dr.S.ALBERTALEXANDER-SELECT-
VIT 9

10. Analysis
Dr.S.ALBERTALEXANDER-SELECT-
VIT 10
Vn= ZnIn=0
 The voltage across the neutral wire is zero
 The neutral line can thus be removed without affecting the
system
 In fact, in long distance power transmission, conductors in
multiples of three are used with the earth itself acting as
the neutral conductor
 Power systems designed in this way are well grounded at
all critical points to ensure safety
 While the line current is the current in each line, the phase
current is the current in each phase of the source or load
 In the Y-Y system, the line current is the same as the
phase current

11. Exercise-1
Calculate the line currents in the three-wire Y-Y system.
SOLUTION
Van
 Ia= ZY
11000 11000 11000
= (5−j2)(10+j8)= 15+j6 = 16.15521.80
0
= 6.81−
21.8 A
 Source voltages are in +ve sequence
 Ib= Ia−1200= 6.81−141.80 A
 Ic= Ia−2400 = 6.81−261.80 A = 6.8198.20 A
Dr.S.ALBERTALEXANDER-SELECT-
VIT 11

12. Exercise 2
A three phase star connected supply system delivering power
to three phase star connected load. The voltage in star
connected supply system between lines is 415 V, 50 Hz ac
supply. The load is balanced load and its load impedance per
phase is (8+j20) Ω. For the given load, calculate (i) Line and
phase currents (ii) active power (iii) Reactive power (iv) power
factor (v) Apparent power.
SOLUTION
(i) Phase current, Iph = Vph
Z
I 338.8 338.800
ph = 8+j20 = 21.5468.20
0
ph L
I =15.72 −
68.2 A and I =
Iph
2
=
15.72
2
=11.12 A
VL (rms)=415 V
ph (rms) 3
V =415 = 239.6
Vph-R= 239.6 2 00 =338.0 00
Vph-Y= 338.0 −1200
Vph-B= =338.0 1200
Dr.S.ALBERTALEXANDER-SELECT-
VIT 12

13. Exercise 2 (Contd..)
 (ii) Active power: 3 VLIL cos = 3 (415)(11.12) cos(68.2)
= 2969 W
 (iii) Reactive power: 3 VLILsin= 3 (415)(11.12) sin (68.2)
= 7421 VAR
 (iv) power factor: cos(68.2) = 0.371 (lagging)
 (v) Apparent power= 3 VLIL= 3 (415)(11.12)= 7993 VA
Dr.S.ALBERTALEXANDER-SELECT-
VIT 13

14. (ii) Balanced Delta-Delta Connection
 A balanced system - is one in which both the balanced
source and balanced load are -connected
Dr.S.ALBERTALEXANDER-SELECT-
VIT 14

15. Analysis
 Assuming the positive sequence, the phase voltages Vab=
Vp00; Vbc= Vp-1200 and Vca= Vp-2400 or Vp+1200
 The line voltages are same as the phase voltages
 Assuming there is no line impedances, the phase voltages
of the delta connected source are equal to the voltages
,
across the impedances: Vab=VAB , Vbc=VBC and Vca= VCA
 The phase currents are:
IAB=VAB= Vab
Z Z
IBC=VBC = Vbc
Z Z
ICA
=VCA = Vca
Z Z
Dr.S.ALBERTALEXANDER-SELECT-
VIT 15

16. Analysis
 Apply KCL at nodes A,B,C, we obtain the line currents as,
 Ia=IAB-ICA, Ib=IBC-IAB, Ic=ICA-IBC
 Each line current lags the corresponding phase current by
300
 Magnitude of the line current is 3 times the magnitude of
the phase current or IL= 𝟑 Ip
 An alternative way of analyzing the - circuit is to convert
both the source and the load to their Y equivalents
Y
Z =Z
Dr.S.ALBERTALEXANDER-SELECT-
VIT 16
3

17. Exercise-4
A balanced -connected load having an impedance 20-j15 
is connected to a -connected, positive-sequence generator
having Vab=33000 V. Calculate the phase currents of the
load and the line currents.
SOLUTION
Phase currents:
VAB
 IAB= Z
=
33000
20−j15
=
33000
25−36.87 0
0
= 13.236.87 A
 IBC= IAB−1200 = 13.2-83.130 A
 ICA= IAB−2400 = 13.2156.870 A
Line currents:
3-30 = 22.86 6.87 A
Dr.S.ALBERTALEXANDER-SELECT-
VIT 17
 Ia= IAB 3-30= (13.236.870 )
 Ib= Ia−1200= 22.86 -113.13 A
 Ic= Ia−2400= 22.86 126.87 A

18. SUMMARY
Type Phase
voltages
Phase currents Line voltages Line currents
Y-Y Van= Vp00
Vbn= Vp-1200
Vcn= Vp-2400
Same as line
currents
Vab = 3Vp300
Vbc= Vab -1200
Vca= Vab +1200
I =Van
a ZY
Ib=Ia−1200
Ic=Ia+1200
- Vab= Vp00
Vbc= Vp-1200
Vca= Vp-2400
I = Vab
AB Z
I= Vbc
BCZ
I= Vca
CA Z
Same as phase
voltage
Ia=IAB 3-300
Ia=Ib-1200
Ia=Ic+1200
Dr.S.ALBERTALEXANDER-SELECT-
VIT 18

19. Dr.S.ALBERTALEXANDER-SELECT-
VIT 19