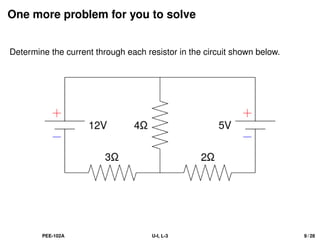
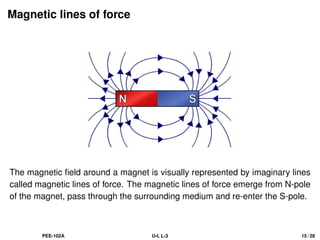
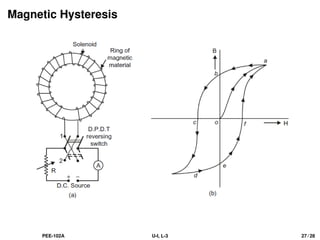
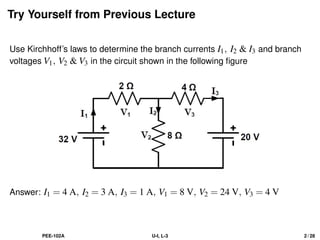
The document provides a comprehensive overview of electrical engineering concepts, specifically focusing on Kirchhoff's laws applied to determine branch currents and voltages in electrical circuits. It also delves into fundamental principles of magnetism, including properties of magnets, laws of magnetic force, and the relationships between magnetic field strength, flux density, and permeability. Key equations and definitions related to these concepts are discussed throughout.

1. PEE-102A
Fundamentals of Electrical Engineering
Lecture-3
Instructor:
Mohd. Umar Rehman
EES, University Polytechnic, AMU
PEE-102A U-I, L-3 1 / 28

2. Try Yourself from Previous Lecture
Use Kirchhoff’s laws to determine the branch currents I1, I2 & I3 and branch
voltages V1, V2 & V3 in the circuit shown in the following figure
Answer: I1 = 4 A, I2 = 3 A, I3 = 1 A, V1 = 8 V, V2 = 24 V, V3 = 4 V
PEE-102A U-I, L-3 2 / 28

3. Solution
Let us first name all the nodes and circuit elements as shown in the following
figure.
PEE-102A U-I, L-3 3 / 28

4. Solution...Contd
Apply KCL at node Q, then we get
PEE-102A U-I, L-3 4 / 28

5. Solution...Contd
Apply KCL at node Q, then we get
I1 = I2 +I3 ...(1)
PEE-102A U-I, L-3 4 / 28

6. Solution...Contd
Apply KVL in the loop PQTUP, then we get
−I1R1 −I2R2 +E1 = 0
PEE-102A U-I, L-3 5 / 28

7. Solution...Contd
Apply KVL in the loop PQTUP, then we get
−I1R1 −I2R2 +E1 = 0
−2I1 −8I2 +32 = 0
PEE-102A U-I, L-3 5 / 28

8. Solution...Contd
Apply KVL in the loop PQTUP, then we get
−I1R1 −I2R2 +E1 = 0
−2I1 −8I2 +32 = 0
I1 +4I2 = 16 ...(2)
PEE-102A U-I, L-3 5 / 28

9. Solution...Contd
Apply KVL in the loop QRSTQ, then we get
−I3R3 −20+I2R2 = 0
PEE-102A U-I, L-3 6 / 28

10. Solution...Contd
Apply KVL in the loop QRSTQ, then we get
−I3R3 −20+I2R2 = 0
−4I3 +8I2 −20 = 0
PEE-102A U-I, L-3 6 / 28

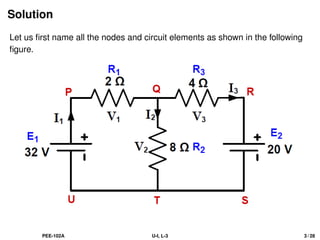
11. Solution...Contd
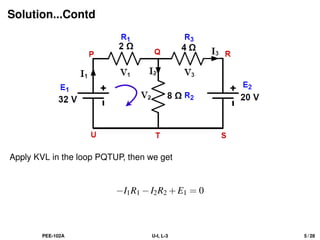
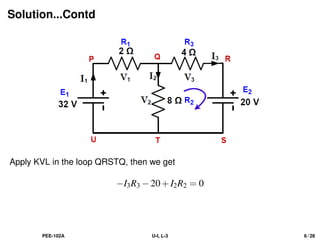
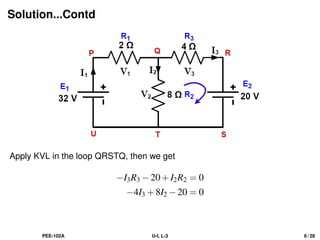
Apply KVL in the loop QRSTQ, then we get
−I3R3 −20+I2R2 = 0
−4I3 +8I2 −20 = 0
−4(I1 −I2)+8I2 = 20 [from Eq.(1)]
PEE-102A U-I, L-3 6 / 28

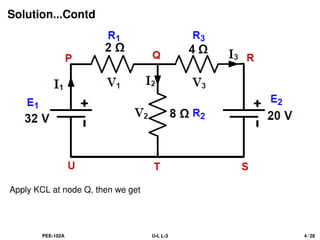
12. Solution...Contd
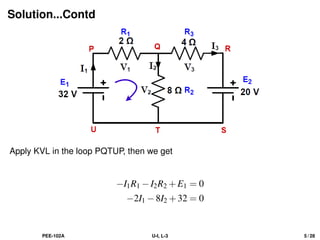
Apply KVL in the loop QRSTQ, then we get
−I3R3 −20+I2R2 = 0
−4I3 +8I2 −20 = 0
−4(I1 −I2)+8I2 = 20 [from Eq.(1)]
−4I1 +12I2 = 20
PEE-102A U-I, L-3 6 / 28

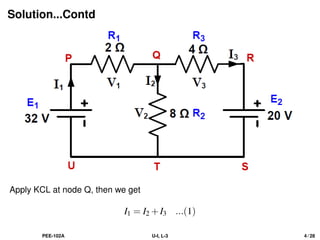
13. Solution...Contd
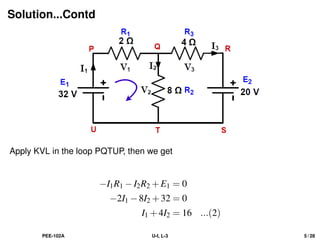
Apply KVL in the loop QRSTQ, then we get
−I3R3 −20+I2R2 = 0
−4I3 +8I2 −20 = 0
−4(I1 −I2)+8I2 = 20 [from Eq.(1)]
−4I1 +12I2 = 20
3I2 −I1 = 5 ...(3)
PEE-102A U-I, L-3 6 / 28

14. Solution...Contd
Adding eq. (2) and (3), we get
(2)+(3)
I1 +4I2 = 16
−
I1 +3I2 = 5
7I2 = 21
I2 = 3 A
Solving for other currents, we get
I1 = 4 A,
I3 = 1 A
PEE-102A U-I, L-3 7 / 28

15. Solution...Contd
And voltages
V1 = I1R1 = 4×2 = 8 V
V2 = I2R2 = 3×8 = 24 V
V3 = I3R3 = 1×4 = 4 V
PEE-102A U-I, L-3 8 / 28

16. One more problem for you to solve
Determine the current through each resistor in the circuit shown below.
PEE-102A U-I, L-3 9 / 28

17. Magnetism
PEE-102A U-I, L-3 10 / 28

18. Magnetism
The word ‘magnet’ comes from the ancient Greek City of Magnesia, where
the natural magnets called lodestones were found.
PEE-102A U-I, L-3 10 / 28

19. Magnetism
The word ‘magnet’ comes from the ancient Greek City of Magnesia, where
the natural magnets called lodestones were found.
Our earth is also a natural magnet.
PEE-102A U-I, L-3 10 / 28

20. Magnetism
The word ‘magnet’ comes from the ancient Greek City of Magnesia, where
the natural magnets called lodestones were found.
Our earth is also a natural magnet.
The property of a magnet by which it attracts certain substances is called
magnetism and the materials which are attracted by a magnet are called
magnetic materials E. g. Fe, Ni, Co.
PEE-102A U-I, L-3 10 / 28

21. Magnetism
The word ‘magnet’ comes from the ancient Greek City of Magnesia, where
the natural magnets called lodestones were found.
Our earth is also a natural magnet.
The property of a magnet by which it attracts certain substances is called
magnetism and the materials which are attracted by a magnet are called
magnetic materials E. g. Fe, Ni, Co.
Magnetism is the essential underlying physical phenomenon behind all
electrical devices like generators, motors etc.
PEE-102A U-I, L-3 10 / 28

22. Magnetism
The word ‘magnet’ comes from the ancient Greek City of Magnesia, where
the natural magnets called lodestones were found.
Our earth is also a natural magnet.
The property of a magnet by which it attracts certain substances is called
magnetism and the materials which are attracted by a magnet are called
magnetic materials E. g. Fe, Ni, Co.
Magnetism is the essential underlying physical phenomenon behind all
electrical devices like generators, motors etc.
The fundamental nature of magnetism is the interaction of moving electric
charges.
PEE-102A U-I, L-3 10 / 28

23. Properties of Magnets
(i) A magnet has two poles i.e. north pole and south pole and the pole
strengths of two poles are same. They point towards the N S poles of
earth when the magnet is suspended freely.
PEE-102A U-I, L-3 11 / 28

24. Properties of Magnets
(i) A magnet has two poles i.e. north pole and south pole and the pole
strengths of two poles are same. They point towards the N S poles of
earth when the magnet is suspended freely.
(ii) The two poles of a magnet cannot be isolated (i.e. separated out)
PEE-102A U-I, L-3 11 / 28

25. Properties of Magnets
(i) A magnet has two poles i.e. north pole and south pole and the pole
strengths of two poles are same. They point towards the N S poles of
earth when the magnet is suspended freely.
(ii) The two poles of a magnet cannot be isolated (i.e. separated out)
(iii) Between magnets, like poles repel and unlike poles attract.
PEE-102A U-I, L-3 11 / 28

26. Properties of Magnets
(i) A magnet has two poles i.e. north pole and south pole and the pole
strengths of two poles are same. They point towards the N S poles of
earth when the magnet is suspended freely.
(ii) The two poles of a magnet cannot be isolated (i.e. separated out)
(iii) Between magnets, like poles repel and unlike poles attract.
(iv) Magnet always attract iron and its alloys.
PEE-102A U-I, L-3 11 / 28

27. Properties of Magnets
(i) A magnet has two poles i.e. north pole and south pole and the pole
strengths of two poles are same. They point towards the N S poles of
earth when the magnet is suspended freely.
(ii) The two poles of a magnet cannot be isolated (i.e. separated out)
(iii) Between magnets, like poles repel and unlike poles attract.
(iv) Magnet always attract iron and its alloys.
(v) The space around a magnet where the influence of the magnet can be
detected in terms of force is known as magnetic field.
PEE-102A U-I, L-3 11 / 28

28. Properties of Magnets
(i) A magnet has two poles i.e. north pole and south pole and the pole
strengths of two poles are same. They point towards the N S poles of
earth when the magnet is suspended freely.
(ii) The two poles of a magnet cannot be isolated (i.e. separated out)
(iii) Between magnets, like poles repel and unlike poles attract.
(iv) Magnet always attract iron and its alloys.
(v) The space around a magnet where the influence of the magnet can be
detected in terms of force is known as magnetic field.
(vi) A magnetic substance itself becomes a magnet when attached to another
magnet.
PEE-102A U-I, L-3 11 / 28

29. Laws of Magnetic Force
PEE-102A U-I, L-3 12 / 28

30. Laws of Magnetic Force
1. Force on a charge in electromagnetic field
PEE-102A U-I, L-3 12 / 28

31. Laws of Magnetic Force
1. Force on a charge in electromagnetic field
~
Fem = ~
Fe +~
Fm
PEE-102A U-I, L-3 12 / 28

32. Laws of Magnetic Force
1. Force on a charge in electromagnetic field
~
Fem = ~
Fe +~
Fm
= q~
E +q
~
v×~
B
PEE-102A U-I, L-3 12 / 28

33. Laws of Magnetic Force
1. Force on a charge in electromagnetic field
~
Fem = ~
Fe +~
Fm
= q~
E +q
~
v×~
B
= q
~
E +~
v×~
B
PEE-102A U-I, L-3 12 / 28

34. Laws of Magnetic Force...Contd
PEE-102A U-I, L-3 13 / 28

35. Laws of Magnetic Force...Contd
2. Coulomb’s law for magnets
PEE-102A U-I, L-3 13 / 28

36. Laws of Magnetic Force...Contd
2. Coulomb’s law for magnets
It is analogous to the Coulomb’s law for charges. It gives an expression for the
force between two magnetic monopoles (isolated hypothetically) whose mag-
netic strengths are m1 and m2, and distance between them is r
~
FC ∝
m1m2
d2
PEE-102A U-I, L-3 13 / 28

37. Laws of Magnetic Force...Contd
2. Coulomb’s law for magnets
It is analogous to the Coulomb’s law for charges. It gives an expression for the
force between two magnetic monopoles (isolated hypothetically) whose mag-
netic strengths are m1 and m2, and distance between them is r
~
FC ∝
m1m2
d2
= K
m1m2
d2
PEE-102A U-I, L-3 13 / 28

38. Laws of Magnetic Force...Contd
2. Coulomb’s law for magnets
It is analogous to the Coulomb’s law for charges. It gives an expression for the
force between two magnetic monopoles (isolated hypothetically) whose mag-
netic strengths are m1 and m2, and distance between them is r
~
FC ∝
m1m2
d2
= K
m1m2
d2
=
1
4πµ
m1m2
d2
PEE-102A U-I, L-3 13 / 28

39. Laws of Magnetic Force...Contd
Where, µ = µ0µr is the permeability of the medium in which the magnetic
monopoles are placed. It gives an idea of ease with which a substance can be
magnetized. The unit of pole strength is Weber (Wb)
PEE-102A U-I, L-3 14 / 28

40. Laws of Magnetic Force...Contd
Where, µ = µ0µr is the permeability of the medium in which the magnetic
monopoles are placed. It gives an idea of ease with which a substance can be
magnetized. The unit of pole strength is Weber (Wb)
µ0 = 4π ×10−7 Tesla-meter/Amp or Henry/meter
PEE-102A U-I, L-3 14 / 28

41. Magnetic lines of force
The magnetic field around a magnet is visually represented by imaginary lines
called magnetic lines of force. The magnetic lines of force emerge from N-pole
of the magnet, pass through the surrounding medium and re-enter the S-pole.
PEE-102A U-I, L-3 15 / 28

42. Magnetic lines ...Contd
Some properties of Magnetic Lines of force:
PEE-102A U-I, L-3 16 / 28

43. Magnetic lines ...Contd
Some properties of Magnetic Lines of force:
(i) Each magnetic line of force forms a closed loop i.e. outside the magnet,
the direction of a magnetic line of force is from north pole to south pole
and it continues through the body of the magnet to form a closed loop.
PEE-102A U-I, L-3 16 / 28

44. Magnetic lines ...Contd
Some properties of Magnetic Lines of force:
(i) Each magnetic line of force forms a closed loop i.e. outside the magnet,
the direction of a magnetic line of force is from north pole to south pole
and it continues through the body of the magnet to form a closed loop.
(ii) No two magnetic lines of force intersect each other. If two magnetic lines
of force intersect, there would be two directions of magnetic field at that
point which is not possible.
PEE-102A U-I, L-3 16 / 28

45. Magnetic lines ...Contd
Some properties of Magnetic Lines of force:
(i) Each magnetic line of force forms a closed loop i.e. outside the magnet,
the direction of a magnetic line of force is from north pole to south pole
and it continues through the body of the magnet to form a closed loop.
(ii) No two magnetic lines of force intersect each other. If two magnetic lines
of force intersect, there would be two directions of magnetic field at that
point which is not possible.
(iii) Where the magnetic lines of force are close together, the magnetic field is
strong and where they are well spaced out, the field is weak.
PEE-102A U-I, L-3 16 / 28

46. Magnetic Flux (φ)
The number of magnetic lines of force in a magnetic field determines the value
of magnetic flux. The more the magnetic lines of force, the greater the magnetic
flux and the stronger is the magnetic field.
Its S. I. unit is Weber (Wb).
PEE-102A U-I, L-3 17 / 28

47. Magnetic Flux Density (B)
The magnetic flux density is defined as the magnetic flux passing normally per
unit area i.e.
B =
φ
A
Its S. I. unit is Wb/m2
or Tesla (T). It is a vector quantity.
PEE-102A U-I, L-3 18 / 28

48. Magnetic Field Strength (H)
Magnetic intensity at any point in a magnetic field is defined as the force acting
on a unit N-pole placed at that point. Its S. I. unit is N/Wb.
Suppose it is desired to find the magnetic intensity at a point P situated at a
distance d metres from a pole of strength m Wb. Imagine a N-pole of 1 Wb is
placed at point P. Then, by definition, magnetic intensity at P is the force acting
on the unit N-pole placed at P i.e.
H =
m×1
4πµd2
=
m
4πµd2
PEE-102A U-I, L-3 19 / 28

49. Permeability (µ)
Permeability of a material means its conductivity for magnetic flux. The greater
the permeability of a material, the greater is its conductivity for magnetic flux
and vice-versa. Air or vacuum is the poorest conductor of magnetic flux. It is
given by
µ = µ0µr
where,
µ = actual permeability of the material
µ0 = absolute permeability of the material = permeability of air/vacuum
µr = relative permeability of the material
The relative permeability of a material is a measure of the relative ease with
which that material conducts magnetic flux compared with the conduction of
flux in air. For air its value is obviously 1. The value of µr for all non-magnetic
materials is also 1. However, relative permeability of magnetic materials is very
high. E. g., soft iron has a relative permeability of 8000.
PEE-102A U-I, L-3 20 / 28

50. Relation Between B and H
The flux density B produced in a material is directly proportional to the applied
magnetizing force H. The greater the magnetizing force, the greater is the flux
density and vice versa
B ∝ H
B = µH = µ0µrH
µ =
B
H
= constant
The ratio
B
H
in a material is always constant and is equal to the absolute per-
meability µ of the material. Suppose a magnetizing force H produces a flux
density B0 in air. Clearly, B0 = µ0H. If air is replaced by some other material
(relative permeability µr) and the same magnetizing force H is applied, then
flux density in the material will be Bmat = µ0µrH.
PEE-102A U-I, L-3 21 / 28

51. Relation Between B and H...Contd
Hence, relative permeability of a material is equal to the ratio of flux density
produced in that material to the flux density produced in air by the same mag-
netizing force. Thus, when we say that µr of soft iron is 8000, it means that for
the same magnetizing force, flux density in soft iron will be 8000 times its value
in air.
PEE-102A U-I, L-3 22 / 28

52. Force on a current carrying conductor lying in a
magnetic field
When a current-carrying conductor is placed at an angle to a magnetic
field, it is found that the conductor experiences a force which acts in a
direction perpendicular to the direction of both the field and the current.
PEE-102A U-I, L-3 23 / 28

53. Force on a current carrying conductor lying in a
magnetic field
When a current-carrying conductor is placed at an angle to a magnetic
field, it is found that the conductor experiences a force which acts in a
direction perpendicular to the direction of both the field and the current.
Consider a straight current-carrying conductor placed in a uniform mag-
netic field as shown in figure.
PEE-102A U-I, L-3 23 / 28

54. Force on a current carrying conductor lying in a
magnetic field
Consider a straight current-carrying conductor of length and carrying cur-
rent placed in a uniform magnetic field of density as shown in figure. Then,
the force is given by:
~
F = i
~
L×~
B
F = iLBsinθ
PEE-102A U-I, L-3 24 / 28

55. Force on a current carrying conductor...Contd
Remarks:
(i) Force is maximum when the conductor is moving perpendicular to the
field lines, i.e. θ = 90◦
(ii) Force is minimum when the conductor is moving parallel to the field lines,
i.e. θ = 0◦ or 180◦
PEE-102A U-I, L-3 25 / 28

56. Magnetisation or B-H Curve
The graph plotted between flux density B and magnetising force H of a
material is called the magnetisation or B-H curve of that material.
The general shape of the B-H curve of a magnetic material is shown in
figure. It can be seen that it is non-linear.
This indicates that the relative permeability µr =
B
µ0H
of a magnetic ma-
terial is not constant but is variable.
The value of µr largely depends upon the value of flux density.
However, the B-H curve for a non-magnetic material, like air will be a
straight line
PEE-102A U-I, L-3 26 / 28

57. Magnetic Hysteresis
PEE-102A U-I, L-3 27 / 28

58. Magnetic Hysteresis
PEE-102A U-I, L-3 27 / 28

59. Magnetic Hysteresis
When a magnetic material is magnetised first in one direction and then in
the other (i.e., one cycle of magnetisation, like in AC supply), it is found that
flux density B in the material lags behind the applied magnetising force H.
This phenomenon is known as magnetic hysteresis.
Hysteresis loss occurs in all the magnetic parts of electrical machines
where there is reversal of magnetisation.
This loss results in wastage of energy in the form of heat, and leads to
undesirable temperature rise.
Hysteresis loss is proportional to the area of the hysteresis loop.
PEE-102A U-I, L-3 28 / 28