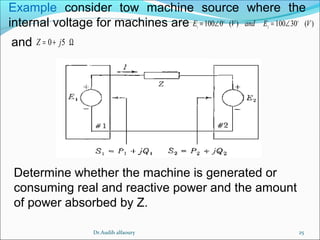
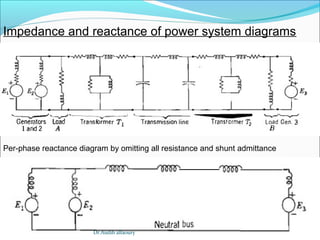
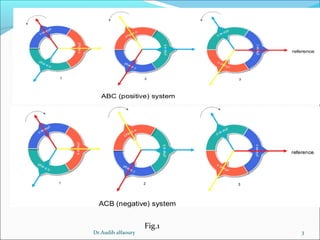
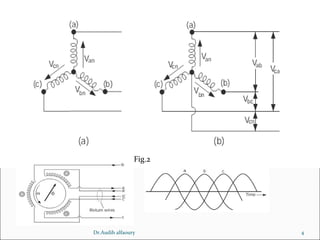
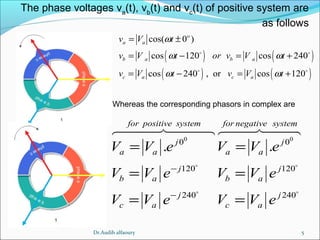
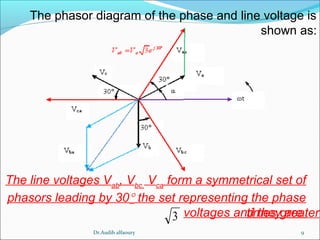
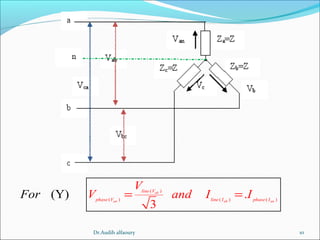
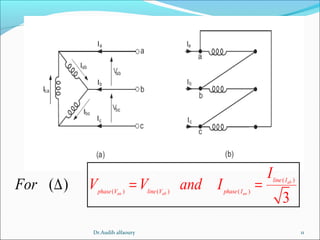
This document summarizes key concepts about three-phase systems. It defines a three-phase system as having three sinusoidal voltages differing in phase by 120 degrees. The voltages can form a positive or negative sequence. Three-phase systems are commonly used for power generation, transmission, and distribution due to their ability to transmit more power with less material. Formulas are provided for calculating line voltages, currents, and power in balanced and unbalanced three-phase systems. Advantages of three-phase systems like constant torque and easier starting of motors are also discussed.

1. Dr Audih al-faoury
Philadelphia university
Electrical department
2014-2015
1Dr.Audih alfaoury

2. Basics Concepts
Three-phase systems
1. Introduction: Three-phase systems are commonly
used in generation, transmission and distribution of
electric power. A three-phase system is a generator
and load pair, in which the generator produces three
sinusoidal voltages of equal magnitude and frequency
but differing in phase by 120° from each other. And
the system may be positive (ABC) or negative (ACB)
Fig 1. The three phase system may be 3 wires no
neutral point or 4 wires system with neutral point .
2Dr.Audih alfaoury

3. 3
Fig.1
Dr.Audih alfaoury

4. 4
Fig.2
Dr.Audih alfaoury

5. 5
The phase voltages va
(t), vb
(t) and vc
(t) of positive system are
as follows
Whereas the corresponding phasors in complex are
( ) ( )
( ) ( )
cos( 0 )
cos 120 cos 240
cos 240 , or cos 120
o
a a
b a b a
c a c a
v V t
v V t or v V t
v V t v V t
ω
ω ω
ω ω
= ±
= − = +
= − = +
o o
o o
0 0
0 0
120 120
240 240
. .
for positive system for negative system
j j
a a a a
j j
b a b a
j j
c a c a
V V e V V e
V V e V V e
V V e V V e
−
−
= =
= =
= =
o o
o o
6447448 6447448
Dr.Audih alfaoury

6. 6
I
V
Z
I
V
Z
I
V
Z
a
a
b
b
c
c
= = =
( )I I I I
Z
V V Vn a b c a b c= + + = + +
1
For three-phase system if all impedances are
identical, Za
= Zb
= Zc
= Z ,then Such a load is called a
balanced load and the currents are:
.
For the figure above by using KCL, we have
In
Ia ZaVa
Ic ZcVc
Ib ZbVb
Dr.Audih alfaoury

7. 7
( )
( )
[ ]
0 120 240
n
cos0 sin0 cos120 sin120 cos240 sin 240
1 3 1 3
1 0 0.
2 2
:
( ) ,
I 0
22
o
j j j
a b c a
o o
a
a
where
Setting the result for curren
V V
t
V V e e e
KCL in the circuit before we obtai
V j
n
V j j j
j
− −
+ + = + + =
= + + − + − =
 
= + − − − + = ÷ ÷
 
=
o o
o o o o
Since the current flowing though the fourth wire is zero, the neutral wire can be
removed and the system is named three wires system
n’n
Ia ZVa
Ic ZVc
Ib ZVb
Dr.Audih alfaoury

8. 8
To determine the line voltages Vab
, Vbc
, Vca
and
relation with phase voltage . Using KVL, we obtain
( ) ( ) ( )
1
1
30
0 120
3
2tan2 32
2
2 3 22 tan .
2 3
cos0 sin0 cos120 sin120
1 3 3 3 3 3
(1 0) ( )
2 2 2 2 2 2
3 3
.
2
3
2
o o
j j o o o o
a b a a
j
a aa
j
ab
j
aa
V V V V e e V j j
V j V j V e
V e V e
−
−
−
 
 ÷
 ÷
 ÷
 ÷
 
 
 ÷ ÷
 
 = − = − = + − + = 
      
= + − − − = + = + = ÷  ÷  ÷ ÷
      
  
= + = ÷ ÷
   
o
30
3 j
ab aV V e=
o
30
30
3
3
j
bc b
j
ca c
V V e
V V e
 =

=
o
o
.
Similarly ;
180
ab
* 180 ;
180
o
o
ab ba
j o
ba ab ab
note V V reversing the subscripts of the voltage or current gives out of the original
V V e V V
≠
= = ∠ = −
Dr.Audih alfaoury

9. 9
The phasor diagram of the phase and line voltage is
shown as:
The line voltages Vab
, Vbc,
Vca
form a symmetrical set of
phasors leading by 30° the set representing the phase
voltages and they are3 times greater.
Dr.Audih alfaoury

10. 10
( )
( ) ( ) ( )
.
3
(Y) ab
an ab an
line V
phase V line I phase I
V
V and I IFor = =
Dr.Audih alfaoury

11. 11
( )
( ) ( ) ( )
(
3
) ab
an ab an
line I
phase V line V phase I
I
V V andor IF = =∆
Dr.Audih alfaoury

12. For the side we get
( ) ( )
(2 )
Since 0
Hence 3
3
T
1
3
herefo 3re
ab Y a b ca Y c a
ab ca Y a b c
a b c a b c
ab ca Y a
ab c
Y
Y
a
Y
a
Y
V Z I I V Z I I
V V Z I I I
I I I I I I
V V Z I
V V
Z
Z
orZ
I
Z Z
Z
∆ ∆
∆
= − = −
− = − −
+ + = ⇒ = − −
=
− =
=
−
= =
12Dr.Audih alfaoury

13. 13
Example: A balance 3Φ system has Vab=173.2 0o
V and a(Y) load is connected with ZL=10 20o
.Assuming ABC system find the voltage and
current for all phases.
Solution:
[ ] [ ] [ ]
[ ] [ ] [ ]
[ ]
[ ]
173.2 0 V , 173.2 240 V , 173.2 120 V
173.2 173.2 173.2
0 30 V , 240 30 V , 120 30 V
3 3 3
:
100 30
10 50 A
10 20
100 210
10 190 A
10 20
100
o o o
ab bc ca
o o o o o o
an bn cn
o
oan
an o
L
o
obn
bn o
L
an
an
L
V V V
V V V
And the current is
V
I
Z
V
I
Z
V
I
Z
= ∠ = ∠ = ∠
= ∠ − = ∠ − = ∠ −
∠ −
= = = ∠ −
∠
∠
= = = ∠
∠
= = [ ]
90
10 70 A
10 20
o
o
o
∠
= ∠
∠
Vab
Dr.Audih alfaoury

14. 14
Three-phase unbalanced system
c
b
a
Vn
Zn
c’
a’
b’
Zp
Zp
Zp
In
n’
n
Ia Za
Va
Ic ZcVc
Ib
ZbVb
If the load impedance Z are not identical, an unbalanced
system is produced. An unbalanced Y-connected system
is shown in Figure. Now we consider a more realistic case
where the wires are represented by impedances Zp
and the
neutral wire connecting n and n’ is represented by
impedance Zn
.
Dr.Audih alfaoury

15. 15
Using the node n as referance, we express the currents Ia
, Ib
, Ic
and In
in
terms of the node voltage Vn
I
V V
Z Z
a
a n
a p
=
−
+
I
V V
Z Z
b
b n
b p
=
−
+
I
V V
Z Z
c
c n
c p
=
−
+
I
V
Z
n
n
n
=
.
The node equation (In
=Ia
+Ib
+Ic
=0), then; In
-Ia
-Ib
-Ic
=0.Thus;
V
Z
V V
Z Z
V V
Z Z
V V
Z Z
n
n
a n
a p
b n
b p
c n
c p
−
−
+
−
−
+
−
−
+
= 0
Solving this equation for Vn
V
V
Z Z
V
Z Z
V
Z Z
Z Z Z Z Z Z Z
n
a
a p
b
b p
c
c p
n a p b p c p
=
+
+
+
+
+
+
+
+
+
+
+
1 1 1 1
Dr.Audih alfaoury

16. 16
Example:
For the network of Figure draw the phasor diagram showing
voltages and currents and write down expressions for total line
currents Ia, Ib,Ic, and the neutral current In.
Solution:
Note that the power factor of the three-phase load is
expressed with respect to the phase current and voltage.
Dr.Audih alfaoury

17. 17Dr.Audih alfaoury

18. 18
Power in three-phase circuits
In the balanced systems, the average power consumed by
each load branch is the same and given by
cosav eff eff
P V I φ=%
The total average power consumed by the three phase load is
the sum of those consumed by each branch, hence, we have
* where Veff
is the effective value of the phase voltage, Ieff
is the effective value of the phase current and φ
is the angle of the impedance
3 3 cosav av eff eff
P P V I φ= =%
( )Leffeff II =
( ) effLeff V3V =
In the balanced Y systems, the phase current has the same magnitude
as the line current , and the line voltage has the effective value
which is:
( )
( ) ( ) ( )3 cos 3 c s
3
o
eff L
av eff L eff effL L
V
P V II φ φ= =
Dr.Audih alfaoury

19. 19
In power term the active power is: [ ]3 . cos ,LLLLP V I Wφ=
( ) ( )3 sinav eff effL L
Q V I φ=
[ ]3 . sin ,LL LL
Q V I VArφ=In power term the reactive is:
.
Same for reactive power
The square root of the sum of (P) and (Q) is the apparent power (S)
[ ]2 2 2 2
( . cos ) ( . sin ) ,S P jQ P Q V I V I V I VAφ φ= + = + = + =
1
2 2
cos , .sin
,and cos cos(tan )
cos sin
From powe triangle we have P S Q S
P Q Q P P
S
P S P Q
φ φ
φ
φ φ
−
= =
= = = = =
+
Dr.Audih alfaoury

20. Advantages of 3φ Power
Can transmit more power for same amount of
wire (twice as much as single phase).
Total torque produced by 3φ machines is
constant, so less vibration.
Three phase machines use less material for same
power rating.
Three phase machines start more easily than
single phase machines.
20Dr.Audih alfaoury

21. 21
Complex power:
If the voltage and current are expressed as:
V V and I Iα β= ∠ = ∠
Then the product of the voltage and current is the apparent
power and in polar form is:
*
. j j
S V I P jQ V e I e V Iα β
α β−
= = − = × = ∠ −
This quantity called the complex power and in rectangular
form is :
( ) ( )*
. .cos .sinS V I V I V Iα β α β= = − + −
Dr.Audih alfaoury

22. 22
Current and voltage at synchronous machine
1- If the synchronous machine working as generator and
since the internal impedance in which the resistance is
very small compared with its reactance ,then the
resistance may be neglected and Z=jX, the internal
voltage and current become: :
.
.
, ,
a a g a
a a g a
a a
a
b c b c
n a b c
E V jX I
V E jX I
E V
I
jX
Same for V V I and I
I I I I
=
=
−
= +
+
+
−
=
Dr.Audih alfaoury

23. 23
2- If the synchronous machine working as motor
The internal voltage and current become: :
.
.
, ,
a a m a
a a m a
a a
a
m
a
a
m
b c b c
n a b c
E V jX I
V E jX I
E V
I
jX
if the E= 0,then
V
I
jX
Same for V V I and I
I I I I
=
=
+
=
=
=
−
+ +
+
Dr.Audih alfaoury

24. 24
Direction of power flow
The relation between P,Q ,bus voltage or generated
voltage with respect to P and Q signs is important
because the direction inform us whether the power
flow is being generated or absorbed (with V and I are
specified).
Dr.Audih alfaoury

25. 25
1 2
100 0 ( ) 100 30 ( )o o
E V and E V= ∠ = ∠
0 5Z j= + Ω
Example consider tow machine source where the
internal voltage for machines are
and
Determine whether the machine is generated or
consuming real and reactive power and the amount
of power absorbed by Z.
Dr.Audih alfaoury

26. 26
Solution:
1 2
(100 0) (86.6 j50 13.4 50
10 2.68 10.35 195
5 5
oE E j j
I j A
Z j j
− + − + −
= = = = − − = ∠
Since the current is from 1 to 2 then for 1 is (-I ) and
for 2 is (+I ),then:
* *
1 1 1 1
*
2 2 2 2
1 2
1 2
( ) 100(10 2.68) 1000 268 VA
( ) (86.6 50)( 10 2.68) 1000 j268
1000 1000 0 W
= 268 268 53 r
V
6 va
A
S P jQ E I j j
S P j
P P P
Q Q Q
Q E I j j
= + = − = + = −
= + = = + − + = − −
= + = − =
+ = − − = −
Dr.Audih alfaoury

27. 27
Machine 1: (P) is positive and (Q) is negative
then the machine consumed active power and
delivered reactive power (motor).
Machine 2: (P)is negative and ( Q) is negative
then machine generate active power and
delivered reactive power ( generator).
The sum of active power is zero ,which
means the load connected between tow
machine consumed reactive power with 536
var which required the reactance of 5 Ω.
Dr.Audih alfaoury

28. 28
Operator (a): Is designate to reduce the angle calculation,
such the operator is a complex number of unit magnitude
and angle of 120o
and define as:
120
2 240
3 360
2
1 120 1. 1(cos120 sin120 ) 0.5 0.866
1 240 1. 1(cos240 sin 240 ) 0.5 0.866
1 360 1. 1(cos360 sin360 ) 1 0 1 0
1 0
o
o
o
o j o o
o j o o
o j o o o
a e j j
a e j j
a e j j
a a
= ∠ = = + = − +
= ∠ = = + = − −
= ∠ = = + = + = ∠
+ + =
Dr.Audih alfaoury

29. 29Dr.Audih alfaoury

30. 30
Impedance and reactance of power system diagrams
Per-phase reactance diagram by omitting all resistance and shunt admittance
Dr.Audih alfaoury

31. 31
Exercises
1 120 45 100 15
. .
o
a b
ab
In a sigle circuit V and V with respect
to a referance node o Find V in polar form
− = ∠ = ∠−
2 2 2
2
1 , 1 , ,
Evaluate the following in polar form
a a a a a j ja a
−
− − + + + +
3 120 210 V
10 60 A.
.
o
an
o
an
A voltage source E and current through the source
is given by I Find the values of P and Q also state wether
the source is delivering or receiving each
− = − ∠
= ∠
4 1 2 0 5
.
If the impedance between machines and in the figure Z j
determine :
a) whether each machine in generating or comsuming power.
b)whether each machine is receiving or supplying
positive reactor power and the amount
c)the value of
− = − Ω
.P and Q absorbed by the impedance
Dr.Audih alfaoury

32. 32
5 10 15 3
208 .
.
o
ca
Three identical impedances of are Y connected to balanced
line voltages of V Specify all the line and phase voltage and the current
as phasors in polar form withV as reference for a phase sequance of abc
φ− ∠ − Ω
6 3 10 30 .
416 90 , .
o
o
bc cn
In abalanced system the Y connected impedances are
If V V specify I in polar form
φ− − ∠ Ω
= ∠
7 15
8 6 .
2 5
110
A balanced load consisting of pure resistances of per phase is
in parallel with abalanced Y load having phase impedances of j
Identical impedances of j are in each of the three lines conneting
the combined loads to a V thr
− ∆ Ω
+ Ω
+ Ω
ee phase supply.Find the current draw
form the supply and line voltage at the combined loads.
Dr.Audih alfaoury