Download as PDF, PPTX
Uploaded byMohammad Umar Rehman
PEE-102A_L-2
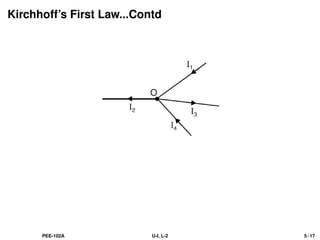
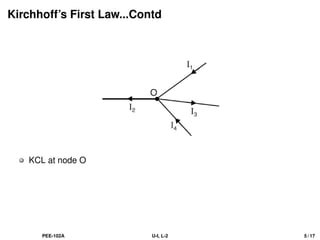
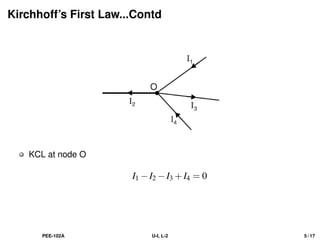
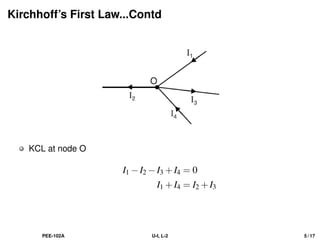
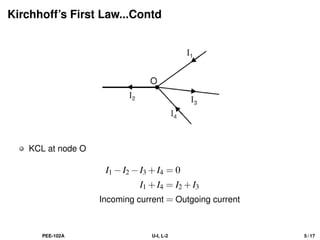
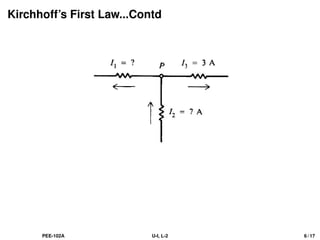
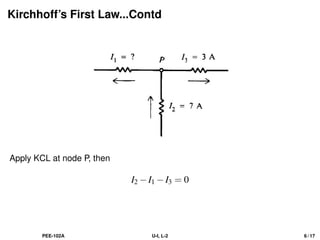
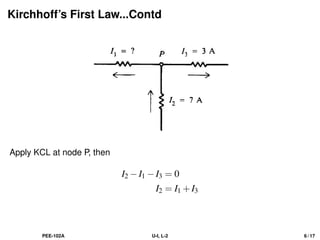
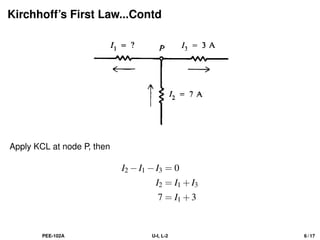
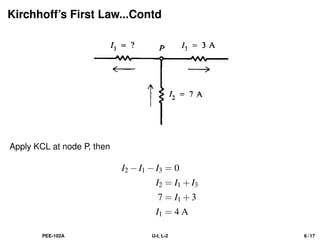
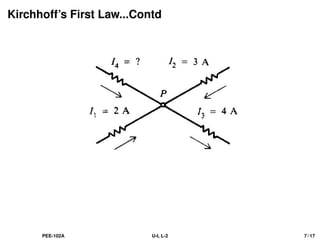
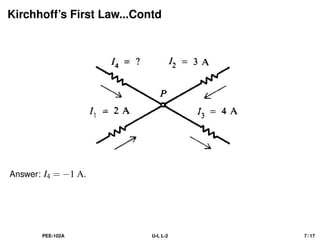
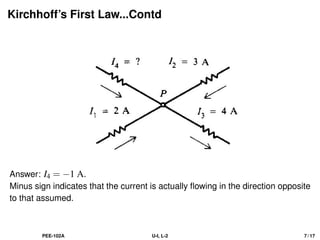
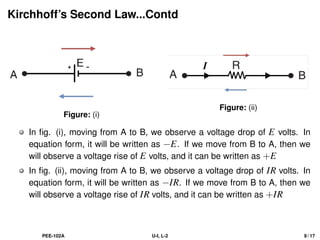
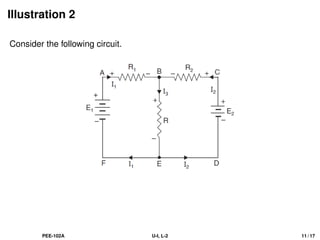
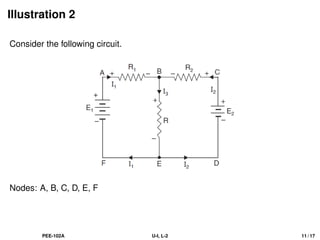
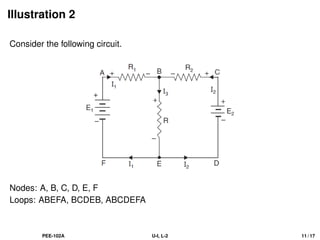
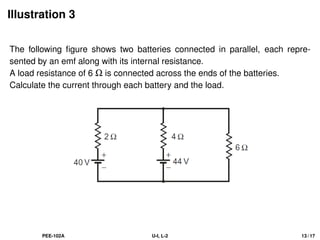
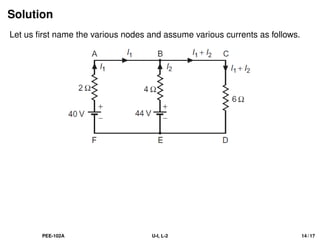
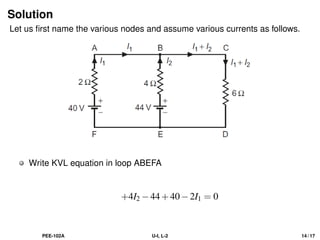
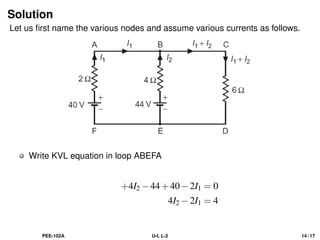
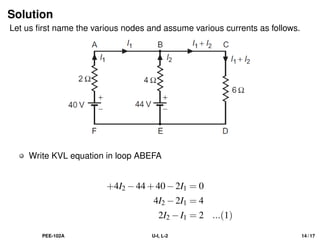
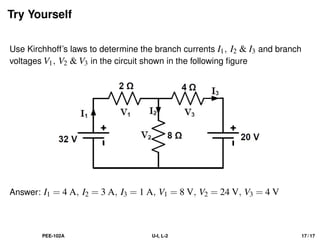
The document discusses Kirchhoff's laws, including the current law (KCL) and the voltage law (KVL), which are based on the conservation of charge and energy, respectively. It provides mathematical formulations of these laws, illustrations of their application in circuit analysis, and examples to calculate currents and voltages in given circuits. Additionally, it emphasizes the significance of these laws in understanding electrical circuits and solving related problems.
More Related Content
PEE-102A_L-2
- 1. PEE-102A Fundamentals of ElectricalEngineering Lecture-2 Instructor: Mohd. Umar Rehman EES, University Polytechnic, AMU PEE-102A U-I, L-2 1 / 17
- 2.
- 3. Circuit Terminology Please seethe following link before Lecture-2: Khan Academy PEE-102A U-I, L-2 3 / 17
- 4. Kirchhoff’s First Law Alsoknown as Kirchhoff’s Current Law (KCL) Based on the conservation of charge. The algebraic sum of currents at a node is zero. Mathematically, we can write ∑ node i = 0 Sign convention: Incoming currents are taken as positive, while outgoing currents are taken as negative. PEE-102A U-I, L-2 4 / 17
- 5. Kirchhoff’s First Law...Contd PEE-102AU-I, L-2 5 / 17
- 6. Kirchhoff’s First Law...Contd KCLat node O PEE-102A U-I, L-2 5 / 17
- 7. Kirchhoff’s First Law...Contd KCLat node O I1 −I2 −I3 +I4 = 0 PEE-102A U-I, L-2 5 / 17
- 8. Kirchhoff’s First Law...Contd KCLat node O I1 −I2 −I3 +I4 = 0 I1 +I4 = I2 +I3 PEE-102A U-I, L-2 5 / 17
- 9. Kirchhoff’s First Law...Contd KCLat node O I1 −I2 −I3 +I4 = 0 I1 +I4 = I2 +I3 Incoming current = Outgoing current PEE-102A U-I, L-2 5 / 17
- 10. Kirchhoff’s First Law...Contd PEE-102AU-I, L-2 6 / 17
- 11. Kirchhoff’s First Law...Contd ApplyKCL at node P, then I2 −I1 −I3 = 0 PEE-102A U-I, L-2 6 / 17
- 12. Kirchhoff’s First Law...Contd ApplyKCL at node P, then I2 −I1 −I3 = 0 I2 = I1 +I3 PEE-102A U-I, L-2 6 / 17
- 13. Kirchhoff’s First Law...Contd ApplyKCL at node P, then I2 −I1 −I3 = 0 I2 = I1 +I3 7 = I1 +3 PEE-102A U-I, L-2 6 / 17
- 14. Kirchhoff’s First Law...Contd ApplyKCL at node P, then I2 −I1 −I3 = 0 I2 = I1 +I3 7 = I1 +3 I1 = 4 A PEE-102A U-I, L-2 6 / 17
- 15. Kirchhoff’s First Law...Contd PEE-102AU-I, L-2 7 / 17
- 16. Kirchhoff’s First Law...Contd Answer:I4 = −1 A. PEE-102A U-I, L-2 7 / 17
- 17. Kirchhoff’s First Law...Contd Answer:I4 = −1 A. Minus sign indicates that the current is actually flowing in the direction opposite to that assumed. PEE-102A U-I, L-2 7 / 17
- 18. Kirchhoff’s Second Law Alsoknown as Kirchhoff’s Voltage Law (KVL) Based on the conservation of energy. The algebraic sum of voltages in a closed loop is zero. Mathematically, we can write ∑ loop v = 0 Sign convention: Voltage rise is taken as positive, while voltage drop is taken as negative. Another form is: Voltage Rise = Voltage drop PEE-102A U-I, L-2 8 / 17
- 19. Kirchhoff’s Second Law...Contd Figure:(i) Figure: (ii) In fig. (i), moving from A to B, we observe a voltage drop of E volts. In equation form, it will be written as −E. If we move from B to A, then we will observe a voltage rise of E volts, and it can be written as +E In fig. (ii), moving from A to B, we observe a voltage drop of IR volts. In equation form, it will be written as −IR. If we move from B to A, then we will observe a voltage rise of IR volts, and it can be written as +IR PEE-102A U-I, L-2 9 / 17
- 20. Illustration 1 Consider thebasic circuit as shown in the following figure. V R I A B C D Moving from A to B, we observe a voltage rise of +V volts. From B to C, no change in voltage, as no component is connected. From C to D, we observe a voltage drop of IR volts. From D to A, no change Thus, we can write the KVL equation in loop ABCDA as: +V −IR = 0 V = IR Hence, we can say that, Ohm’s law is a special case of KVL. Same equation will be obtained if we move in any other direction PEE-102A U-I, L-2 10 / 17
- 21. Illustration 2 Consider thefollowing circuit. PEE-102A U-I, L-2 11 / 17
- 22. Illustration 2 Consider thefollowing circuit. Nodes: A, B, C, D, E, F PEE-102A U-I, L-2 11 / 17
- 23. Illustration 2 Consider thefollowing circuit. Nodes: A, B, C, D, E, F Loops: ABEFA, BCDEB, ABCDEFA PEE-102A U-I, L-2 11 / 17
- 24. Illustration 2...Contd KCL atnode B: I1 +I2 −I3 = 0 PEE-102A U-I, L-2 12 / 17
- 25. Illustration 2...Contd KCL atnode B: I1 +I2 −I3 = 0 KCL at node E: I3 −I1 −I2 = 0 PEE-102A U-I, L-2 12 / 17
- 26. Illustration 2...Contd KCL atnode B: I1 +I2 −I3 = 0 KCL at node E: I3 −I1 −I2 = 0 KVL in loop ABEFA: −I1R1 −I3R+E1 = 0 PEE-102A U-I, L-2 12 / 17
- 27. Illustration 2...Contd KCL atnode B: I1 +I2 −I3 = 0 KCL at node E: I3 −I1 −I2 = 0 KVL in loop ABEFA: −I1R1 −I3R+E1 = 0 KVL in loop BCDEB: +I2R2 −E2 +I3R = 0 PEE-102A U-I, L-2 12 / 17
- 28. Illustration 2...Contd KCL atnode B: I1 +I2 −I3 = 0 KCL at node E: I3 −I1 −I2 = 0 KVL in loop ABEFA: −I1R1 −I3R+E1 = 0 KVL in loop BCDEB: +I2R2 −E2 +I3R = 0 KVL in loop ABCDEFA: −I1R1 +I2R2 −E2 +E1 = 0 PEE-102A U-I, L-2 12 / 17
- 29. Illustration 2...Contd KCL atnode B: I1 +I2 −I3 = 0 KCL at node E: I3 −I1 −I2 = 0 KVL in loop ABEFA: −I1R1 −I3R+E1 = 0 KVL in loop BCDEB: +I2R2 −E2 +I3R = 0 KVL in loop ABCDEFA: −I1R1 +I2R2 −E2 +E1 = 0 The above set of equations can be solved to determine various currents, voltages in the circuit. PEE-102A U-I, L-2 12 / 17
- 30. Illustration 3 The followingfigure shows two batteries connected in parallel, each repre- sented by an emf along with its internal resistance. A load resistance of 6 Ω is connected across the ends of the batteries. Calculate the current through each battery and the load. PEE-102A U-I, L-2 13 / 17
- 31. Solution Let us firstname the various nodes and assume various currents as follows. PEE-102A U-I, L-2 14 / 17
- 32. Solution Let us firstname the various nodes and assume various currents as follows. PEE-102A U-I, L-2 14 / 17
- 33. Solution Let us firstname the various nodes and assume various currents as follows. Write KVL equation in loop ABEFA +4I2 −44+40−2I1 = 0 PEE-102A U-I, L-2 14 / 17
- 34. Solution Let us firstname the various nodes and assume various currents as follows. Write KVL equation in loop ABEFA +4I2 −44+40−2I1 = 0 4I2 −2I1 = 4 PEE-102A U-I, L-2 14 / 17
- 35. Solution Let us firstname the various nodes and assume various currents as follows. Write KVL equation in loop ABEFA +4I2 −44+40−2I1 = 0 4I2 −2I1 = 4 2I2 −I1 = 2 ...(1) PEE-102A U-I, L-2 14 / 17
- 36. Solution...Contd Write KVL equationin loop BCDEB −6(I1 +I2)+44−4I2 = 0 PEE-102A U-I, L-2 15 / 17
- 37. Solution...Contd Write KVL equationin loop BCDEB −6(I1 +I2)+44−4I2 = 0 −10I2 −6I1 = −44 PEE-102A U-I, L-2 15 / 17
- 38. Solution...Contd Write KVL equationin loop BCDEB −6(I1 +I2)+44−4I2 = 0 −10I2 −6I1 = −44 5I2 +3I1 = 22 ...(2) PEE-102A U-I, L-2 15 / 17
- 39. Solution...Contd Multiply Eq. (1)by 3 and add to Eq. (2), then we get 3×(1)+(2) 6I2 − 3I1 = 6 5I2 + 3I1 = 22 11I2 = 28 I2 = 28 11 A Solving for I1, we get I1 = 34 11 A PEE-102A U-I, L-2 16 / 17
- 40. Solution...Contd Multiply Eq. (1)by 3 and add to Eq. (2), then we get 3×(1)+(2) 6I2 − 3I1 = 6 5I2 + 3I1 = 22 11I2 = 28 I2 = 28 11 A Solving for I1, we get I1 = 34 11 A Total current through load = I1 +I2 = 34 11 + 28 11 = 62 11 A PEE-102A U-I, L-2 16 / 17
- 41. Try Yourself Use Kirchhoff’slaws to determine the branch currents I1, I2 I3 and branch voltages V1, V2 V3 in the circuit shown in the following figure Answer: I1 = 4 A, I2 = 3 A, I3 = 1 A, V1 = 8 V, V2 = 24 V, V3 = 4 V PEE-102A U-I, L-2 17 / 17