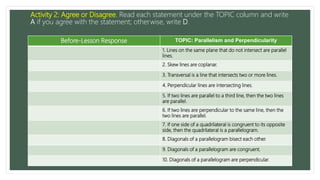
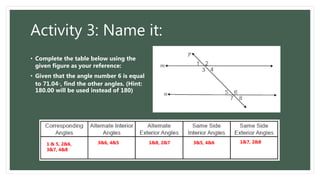
This document contains a math lesson on parallelism and perpendicularity. It includes an opening prayer, activities to identify parallel and perpendicular lines using optical illusions and geometry examples, and a worksheet for students to identify different types of angles and lines related to parallelism and perpendicularity. The goal is to help students understand how to establish whether two lines are parallel or perpendicular.

1. PARALLELISM AND
PERPENDICULARITY

2. Math Prayer
Lord,
You have created us in different shapes and angles
But still you made sure that we are congruent one way or another.
No matter which sides, even if there are terms undefined, your teachings will remain our guide.
May our lesson today maybe made parallel with what you want us to become. And by the time
our paths perpendicularly crossed, may we face you with confidence
That you will shower us with your unending love and providence. AMEN.

3. This lesson seeks to answer the question:
“How can we establish
parallelism or
perpendicularity of lines?”

4. Activity 1: Optical Illusion
• Can you see straight lines in
the picture? ________
• Do these lines meet/intersect?
________
• Are these lines parallel? Why?
________
• Are the segments on the faces
of the prism below parallel?
Why? ________

5. Activity 1: Optical Illusion
• What can you say about the
edges of the prism? ________
• Describe the edges that
intersect and the edges that
do not intersect. ________

6. Activity 2: Agree or Disagree. Read each statement under the TOPIC column and write
A if you agree with the statement; otherwise, write D.
Before-Lesson Response TOPIC: Parallelism and Perpendicularity
1. Lines on the same plane that do not intersect are parallel
lines.
2. Skew lines are coplanar.
3. Transversal is a line that intersects two or more lines.
4. Perpendicular lines are intersecting lines.
5. If two lines are parallel to a third line, then the two lines
are parallel.
6. If two lines are perpendicular to the same line, then the
two lines are parallel.
7. If one side of a quadrilateral is congruent to its opposite
side, then the quadrilateral is a parallelogram.
8. Diagonals of a parallelogram bisect each other.
9. Diagonals of a parallelogram are congruent.
10. Diagonals of a parallelogram are perpendicular.

9. Activity 3: Name it:
• Complete the table below using the
given figure as your reference:
• Given that the angle number 6 is equal
to 71.04◦, find the other angles. (Hint:
180.00 will be used instead of 180)
1 & 5, 2&6,
3&7, 4&8
3&6, 4&5 1&8, 2&7 3&5, 4&6 1&7, 2&8

12. Perpendicular distance
between parallel lines

13. GET READY!

15. 1 and 5, 2 and 6, 3 and 7, 4 and 8
4 and 5, 3 and 6
1 and 8, 2 and 7
4 and 6, 3 and 5
1 and 7, 2 and 8

16. Review on Parallel lines
• Using the figure in Individual Work A p. 301 of your book, Identify
the following (for 65 points). Write your answers in your notebook
• 2 sets of corresponding angles
• 2 sets of alternate interior angles
• 2 sets of alternate exterior angles
• 2 sets of interior side of the transversal
• 2 sets of exterior side of the transversal
• B. Solve: If <10 = 20º find angles 1,2,3,4,9,11, and 12
If < 13 = 17.01º find angles 5,6,7,8,14,15 and 16

18. Given
1 and 3
Definition of Parallel lines