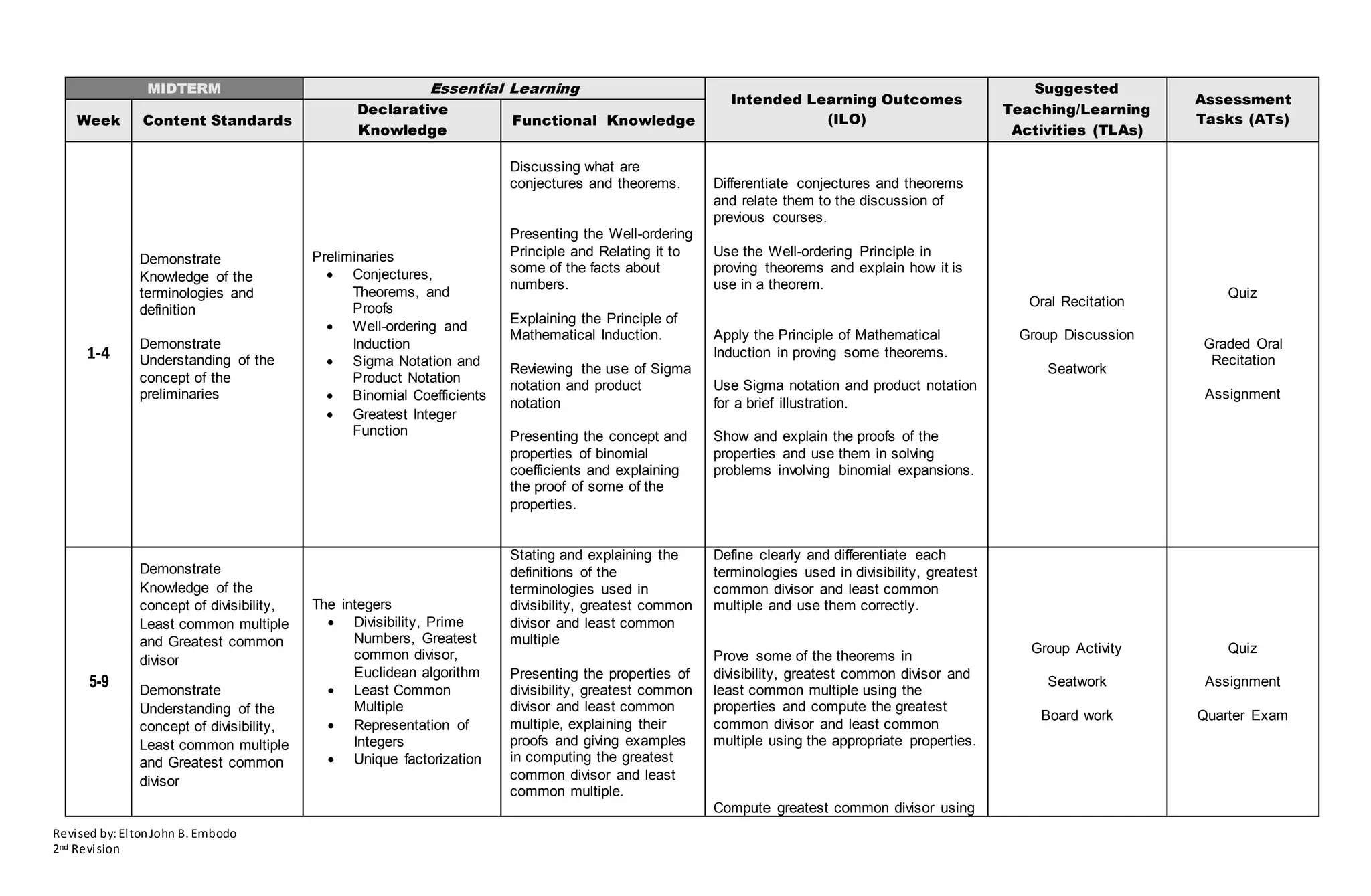
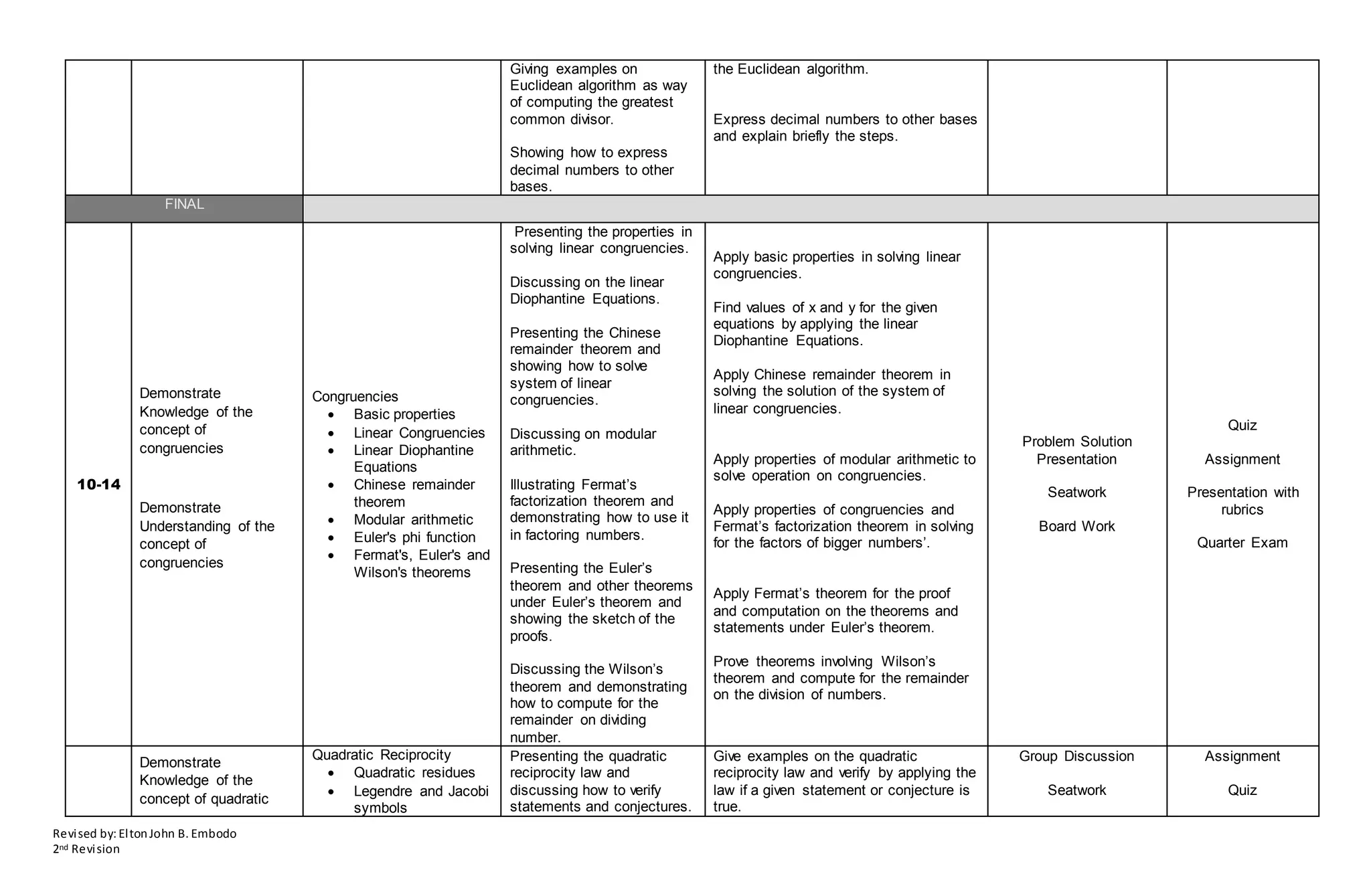
This document outlines an outcomes-based teaching and learning plan for a Number Theory course. The course aims to teach students about properties of numbers and mathematical proofs. Over 15 weeks, students will learn about topics like prime factorization, divisibility rules, congruencies, and quadratic reciprocity. Assessment will include quizzes, assignments, and exams to evaluate students' understanding of key concepts and ability to apply them.

1. Revised by:EltonJohn B. Embodo
2nd Revision
GOV. ALFONSO D. TAN COLLEGE
Bachelor Secondary Education major in Mathematics (BSEd-Math)
Outcomes – Based Teaching and Learning Plan in ME 117
Course Title Number Theory Course Code ME 117
Credit Units 3 Course Pre-/Co-requisites Advanced Algebra, Logic & Set Theory
Course Description This course is a study of the properties of numbers and their proofs. It presents the students with different methods of mathematical proving. It focuses on
the discussion of the set of integers that covers Unique Prime Factorization, Divisibility Rules, Euclidean Algorithm, Linear Congruencies and Linear
Diophantine Equations.
Program Intended
Learning Outcomes
(PILO)
Graduates of BSME programs are teachers who:
a. Articulate the rootedness of education in philosophical, socio cultural, historical, psychological, and political concept
b. Demonstrate mastery of subject matter/discipline
c. Facilitate learning using a wide range of teaching methodologies and delivery modes appropriate to specific learners and their environments
d. Develop innovative curricula, instructional plans, teaching, approaches, and resources for diverse learners.
e. Apply skills in the development and utilization of ICT to promote, quality, relevant, and sustainable educational practices.
f. Demonstrate a variety of thinking skills in planning, monitoring, assessing, and reporting learning processes and outcomes
g. Practice professional and ethical teaching standards sensitive to the local, national, and global realities.
h. Pursue lifelong learning for professional growth through varied experiential and field-based opportunities.
i. Exhibits competence in mathematical concepts and procedures.
j. Exhibit proficiency in relating mathematics to other curricular areas.
k. Manifest meaningful and comprehensive pedagogical content knowledge (PCK) of mathematics.
l. Demonstrate competence in designing, constructing and utilizing different forms of assessment in mathematics.
m. Demonstrate proficiency in problem-solving by solving and creating routine and non-routine problems with different levels of complexity.
n. Use effectively appropriate approaches, methods, and techniques in teaching mathematics including technological tools.
o. Appreciate mathematics as an opportunity for creative work, moments of enlightenment, discovery and gaining insights of the world.
Course Intended
Learning Outcomes
(CILO)
At the end of this course, the students should be able to:
1) effectively express the concepts and results of Number Theory;
2) construct mathematical proofs of statements and find counterexamples to false statements in Number Theory;
3) collect and use numerical data to form conjectures about the integers;
4) understand the logic and methods behind the major proofs in Number Theory;
5) work effectively as part of a group to solve challenging problems in Number Theory.
Alfonsos as Lux Mundi: Serving Humanity with Empowered Mind, Passionate Heart and Virtuous Soul

2. Revised by:EltonJohn B. Embodo
2nd Revision
MIDTERM Essential Learning
Intended Learning Outcomes
(ILO)
Suggested
Teaching/Learning
Activities (TLAs)
Assessment
Tasks (ATs)Week Content Standards
Declarative
Knowledge
Functional Knowledge
1-4
Demonstrate
Knowledge of the
terminologies and
definition
Demonstrate
Understanding of the
concept of the
preliminaries
Preliminaries
 Conjectures,
Theorems, and
Proofs
 Well-ordering and
Induction
 Sigma Notation and
Product Notation
 Binomial Coefficients
 Greatest Integer
Function
Discussing what are
conjectures and theorems.
Presenting the Well-ordering
Principle and Relating it to
some of the facts about
numbers.
Explaining the Principle of
Mathematical Induction.
Reviewing the use of Sigma
notation and product
notation
Presenting the concept and
properties of binomial
coefficients and explaining
the proof of some of the
properties.
Differentiate conjectures and theorems
and relate them to the discussion of
previous courses.
Use the Well-ordering Principle in
proving theorems and explain how it is
use in a theorem.
Apply the Principle of Mathematical
Induction in proving some theorems.
Use Sigma notation and product notation
for a brief illustration.
Show and explain the proofs of the
properties and use them in solving
problems involving binomial expansions.
Oral Recitation
Group Discussion
Seatwork
Quiz
Graded Oral
Recitation
Assignment
5-9
Demonstrate
Knowledge of the
concept of divisibility,
Least common multiple
and Greatest common
divisor
Demonstrate
Understanding of the
concept of divisibility,
Least common multiple
and Greatest common
divisor
The integers
 Divisibility, Prime
Numbers, Greatest
common divisor,
Euclidean algorithm
 Least Common
Multiple
 Representation of
Integers
 Unique factorization
Stating and explaining the
definitions of the
terminologies used in
divisibility, greatest common
divisor and least common
multiple
Presenting the properties of
divisibility, greatest common
divisor and least common
multiple, explaining their
proofs and giving examples
in computing the greatest
common divisor and least
common multiple.
Define clearly and differentiate each
terminologies used in divisibility, greatest
common divisor and least common
multiple and use them correctly.
Prove some of the theorems in
divisibility, greatest common divisor and
least common multiple using the
properties and compute the greatest
common divisor and least common
multiple using the appropriate properties.
Compute greatest common divisor using
Group Activity
Seatwork
Board work
Quiz
Assignment
Quarter Exam

3. Revised by:EltonJohn B. Embodo
2nd Revision
Giving examples on
Euclidean algorithm as way
of computing the greatest
common divisor.
Showing how to express
decimal numbers to other
bases.
the Euclidean algorithm.
Express decimal numbers to other bases
and explain briefly the steps.
FINAL
10-14
Demonstrate
Knowledge of the
concept of
congruencies
Demonstrate
Understanding of the
concept of
congruencies
Congruencies
 Basic properties
 Linear Congruencies
 Linear Diophantine
Equations
 Chinese remainder
theorem
 Modular arithmetic
 Euler's phi function
 Fermat's, Euler's and
Wilson's theorems
Presenting the properties in
solving linear congruencies.
Discussing on the linear
Diophantine Equations.
Presenting the Chinese
remainder theorem and
showing how to solve
system of linear
congruencies.
Discussing on modular
arithmetic.
Illustrating Fermat’s
factorization theorem and
demonstrating how to use it
in factoring numbers.
Presenting the Euler’s
theorem and other theorems
under Euler’s theorem and
showing the sketch of the
proofs.
Discussing the Wilson’s
theorem and demonstrating
how to compute for the
remainder on dividing
number.
Apply basic properties in solving linear
congruencies.
Find values of x and y for the given
equations by applying the linear
Diophantine Equations.
Apply Chinese remainder theorem in
solving the solution of the system of
linear congruencies.
Apply properties of modular arithmetic to
solve operation on congruencies.
Apply properties of congruencies and
Fermat’s factorization theorem in solving
for the factors of bigger numbers’.
Apply Fermat’s theorem for the proof
and computation on the theorems and
statements under Euler’s theorem.
Prove theorems involving Wilson’s
theorem and compute for the remainder
on the division of numbers.
Problem Solution
Presentation
Seatwork
Board Work
Quiz
Assignment
Presentation with
rubrics
Quarter Exam
Demonstrate
Knowledge of the
concept of quadratic
Quadratic Reciprocity
 Quadratic residues
 Legendre and Jacobi
symbols
Presenting the quadratic
reciprocity law and
discussing how to verify
statements and conjectures.
Give examples on the quadratic
reciprocity law and verify by applying the
law if a given statement or conjecture is
true.
Group Discussion
Seatwork
Assignment
Quiz

4. Revised by:EltonJohn B. Embodo
2nd Revision
15– 18
reciprocity
Demonstrate
Understanding of the
concept of the
quadratic reciprocity
Law of quadratic reciprocity
(possibility skip proof to
allow time for other topics)
Showing the definition of
Legendre symbol.
Enumerating the properties
of Legendre symbols and
discussing how to compute
Legendre symbol.
State the definition of Legendre symbol.
Apply the properties of Legendre
symbols in computation of Legendre
symbols.
Solution Presentation Presentation with
rubrics
Final Exam
Basic Readings
Burton, David M., (2005). Elementary Number Theory, Fifth Edition. McGraw-HillPublisher, Singapore.
Extended Readings To be provided
Course Assessment As identifiedin the Assessment Task
Course Policies LanguageofInstructions
English
Attendance
As identifiedin the student handbook
Homework,Quizzes,Written Reports,ReactionPapersand Portfolio
Special Requirement
GradingSystem
SummativeQuiz– 30%
PerformanceTask–40%
PeriodicalExamination –30%
Total
Classroom RulesandRegulations
Respectmustbe observed in the classroom
Committee Members
CommitteeLeader : Clint Joy Quije
Members : Elton John B. Embodo

5. Revised by:EltonJohn B. Embodo
2nd Revision
Consultation Schedule FacultyMember : ClintJoy M. Quije
ContactNumber :
E-mailaddress :
ConsultationHours:
TimeandVenue :
Course Title A.Y. Term of
Effectivity
Prepared by Checked by Approved by Page/s
Number
Theory
2018 – 2019 CLINT JOYM. QUIJE, LPT
Instructor
NORIEL B. ERAP, MEd
Dean, ITE
LOVE H. FALLORAN, MSCRIM
ACA for Academics
5