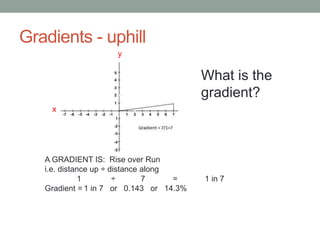
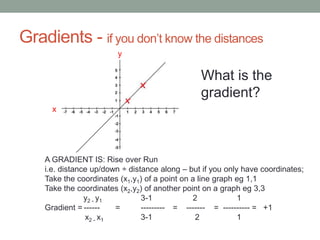
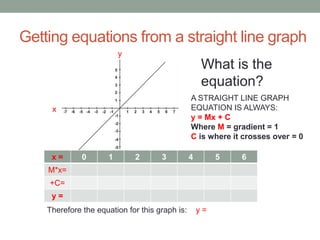
This document discusses functions and linear graphs. It defines functions as relations or expressions involving variables and explains that they are useful in computing for representing problems when all values are unknown. It also covers identifying the gradient and y-intercept of a linear graph from its equation in the form y=mx+c. Key steps shown include calculating the gradient as rise over run and using coordinates to find the equation from a graph.

1. UNIT 18
COMPUTATIONAL
THINKING
P2;
identify linear and quadratic functions
obtain the equation of a straight line from a graph

2. Functions
What are they?
• Why are they useful to us in Computing?

3. Functions
What are they?
“Functions are a relation or expression
involving one or more variables”
i.e They are a way of writing down a
problem or sum when you don’t know all the
figures or answers.
e.g.

4. Functions
Why are functions useful to us in
Computing?
They help us keep clear what we know
and don’t know.
They help us write problems in a way
that start to help us work out the
answer

5. Functions
What are they?
“Functions are a relation or expression involving one or more variables”
i.e They are a way of writing down a problem or sum when you don’t know all the figures or answers.
e.g. here is a simple sum to help us do harder ones later
Two students bought 10 cans of coke
If one student bought 4 cans,
how many were bought by the other student?
We would write it like this;
10 cans bought = (1 * 4 cans) + (1 * x cans)
10 = 4 + x or we can write;
x + 4 = 10 (to get the one thing we need to know (x) on the left)
(Rule to Remember if we move a number to the opposite side we have to change the sign plus (+)
becomes minus (-) and times (x) becomes divide (÷) )
x = 10 – 4
x = 6 so the other student bought 6 cans

6. Functions
Exercise
Two lecturers bought 10 pens
If one lecturer bought 4 pens,
how many were bought by the lecturer?
Write out your working;
…………………………………………………………………………………..
…………………………………………………………………………………..
…………………………………………………………………………………..
…………………………………………………………………………………..
…………………………………………………………………………………..
…………………………………………………………………………………..
…………………………………………………………………………………..
Answer: The other lecturer bought …… pens

7. Functions
It’s your birthday and you are buying cakes for all your group
You decide to buy bakewell tarts which come in boxes of 6.
You have 18 in your group
How many boxe do you need to buy?
We would write it like this;
No of boxes multiplied by 6 per box = 18 tarts (at least)
x * 6 = 18
(we need to know (x) on the left on its own)
(Rule to Remember if we move a number to the opposite side we have to change the sign plus (+)
becomes minus (-) and times (x) becomes divide (÷) )
x = 18 ÷ 6
x = 18/6
x = 3
Answer: I need to buy 3 boxes

8. Functions
Exercise
It’s your birthday and you are buying cakes for all your friends
You decide to buy bakewell tarts which come in boxes of 6.
You have 30 friends
How many boxes do you need to buy?
Write out your working;
…………………………………………………………………………………..
…………………………………………………………………………………..
…………………………………………………………………………………..
…………………………………………………………………………………..
…………………………………………………………………………………..
…………………………………………………………………………………..
…………………………………………………………………………………..
Answer: I need to buy …….. boxes

9. Functions
Exercise
Write out the answers
What are functions?
…………………………………………………………………………………..
…………………………………………………………………………………..
Why are they useful to us in
Computing?
…………………………………………………………………………………..
…………………………………………………………………………………..

10. Graphs – x and y axis
x
y
Graphs let us see figures in a graphical way and
help us understand them more easily.
• There is an x and a y axis marked with their values
• Usually only the top right hand corner with positive
values of x and y is shown

11. Graphs – x and y axis
x
y
Remember the game ‘Battleships’ ?
Battleships have a location based on columns and rows named by
letters and numbers – called coordinates. Eg B7 and A3
Graphs have points with coordinates eg (2,4) (where x=2 and y=4)
• If x = 2 then location of the point is somewhere on the red line
• If y = 4 then location of the point is somewhere on the blue line
If x = 2 and y = 4 then location of the point is exactly where the red
line and the blue line cross (or intersect)

12. Gradients - uphill
x
y
A GRADIENT IS: Rise over Run
i.e. distance up ÷ distance along
1 ÷ 7 = 1 in 7
Gradient = 1 in 7 or 0.143 or 14.3%
What is the
gradient?

13. Gradients - downhill
x
y
A GRADIENT IS: Rise over Run
i.e. distance up ÷ distance along
1 ÷ 7 = 1 in 7
Gradient = 1 in 7 or -0.143 or 14.3%
This is easier for whole numbers but what if the numbers are decimals
What is the
gradient?

14. Gradients - if you don’t know the distances
x
y
A GRADIENT IS: Rise over Run
i.e. distance up/down ÷ distance along – but if you only have coordinates;
Take the coordinates (x1,y1) of a point on a line graph eg 1,1
Take the coordinates (x2,y2) of another point on a graph eg 3,3
y2 - y1 3-1 2 1
Gradient = ------ = --------- = ------- = ---------- = +1
x2 - x1 3-1 2 1
What is the
gradient?

15. Getting equations from a straight line graph
x
y
x = 0 1 2 3 4 5 6
M*x=
+C=
y =
Therefore the equation for this graph is: y =
What is the
equation?
A STRAIGHT LINE GRAPH
EQUATION IS ALWAYS:
y = Mx + C
Where M = gradient = 1
C is where it crosses over = 0

16. Getting the equation from a graph 1
x
y
Therefore the equation for this graph is: y = …………………………..
What is the
equation?
x 0 1 2 3 4 5 6
Mx
+C
y =
A STRAIGHT LINE GRAPH
EQUATION IS ALWAYS:
y = Mx + C
Where M = gradient = 1
C is where it crosses over = 1

17. Getting the equation from a graph 2
x
y
x 0 1 2 3 4 5 6
Mx
+C
y =
Therefore the equation for this graph is: y = …………………………..
A STRAIGHT LINE GRAPH
EQUATION IS ALWAYS:
y = Mx + C
Where M = gradient = 1
C is where it crosses over = 2
What is the
equation?

18. Getting the equations from graphs 3 + 4
x
y
x 0 1 2 3 4 5 6
Mx 1*0 1*1 1*2 1*3 1*4 1*5 1*6
+C
y =
The equation for the Red graph is: y = (1 * x) + …. or y = x + ….
The equation for the Blue graph is: y = (1 * x) + …. or y = x + ….
A STRAIGHT LINE GRAPH
EQUATION IS ALWAYS:
y = Mx + C
Where M = gradient = 1
C is where it crosses over = ?
What is the equation for
the red and blue graphs?

19. Getting the equation from a graph 5
x
y
x 0 1 2 3 4 5 6
Mx
+C
y =
Therefore the equation for this graph is: y = …………………………..
A STRAIGHT LINE GRAPH
EQUATION IS ALWAYS:
y = Mx + C
Where M = gradient = -1
C is where it crosses over = 0
What is the
equation?

20. Getting the equation from a graph 6
x
y
x 0 1 2 3 4 5 6
Mx
+C
y =
Therefore the equation for this graph is: y = …………………………..
A STRAIGHT LINE GRAPH
EQUATION IS ALWAYS:
y = Mx + C
Where M = gradient = -1
C is where it crosses over = 2
What is the
equation?

21. Getting the equation from a graph 7
x
y
x 0 1 2 3 4 5 6
Mx
+C
y =
Therefore the equation for this graph is: y = …………………………..
A STRAIGHT LINE GRAPH
EQUATION IS ALWAYS:
y = Mx + C
Where M = gradient = ………..?
C where it crosses over = …..?
What is the
equation?

22. Well Done!
You have used functions
You have worked out the
equation for a straight line graph