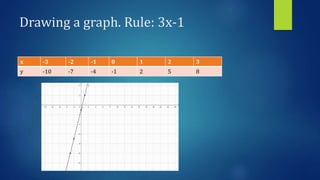
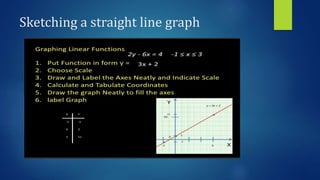
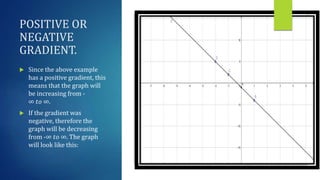
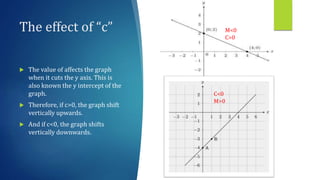
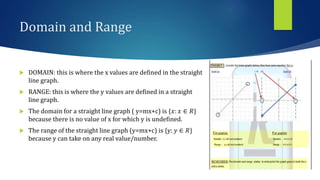
This document discusses linear functions and straight line graphs. It defines key concepts such as the standard form of a linear equation (y=mx+c), where m is the gradient and c is the y-intercept. It explains how to calculate the gradient between two points and interprets positive and negative gradients. The document also covers finding the x-intercept and y-intercept of a line, and defines the domain and range of linear functions.

1. Linear functions.
STRAIGHT LINE GRAPH.

2. RECAP!!!
 SPIDER WEB.
 In a spider web, there are x values, y
values and also a rule.
 On your left, this is where your x-
values(input) lie. Therefore, your y-
values(output) are on the right hand
side.
 Lastly, the rule is always in the
middles.
 The x- and y-values are there to help
one plot a graph on a cartesian plane.
A cartesian plane consist of all the
integers in the number system.

3. Drawing a graph. Rule: 3x-1
x -3 -2 -1 0 1 2 3
y -10 -7 -4 -1 2 5 8

4. Sketching a straight line graph

5. What is a function?
 A function is an expression or rule that defines a relationship between a variable that is
dependent and a variable that is independent.
 In a cartesian plane, the independent variable are the x-values, the dependent variable are
the y-values. The y-values lie on the y axis, and the x-values lie on the x axis (Barek, 2013).
 The standard form/equation of a straight line graph is defined as: 𝑦 = 𝑚𝑥 + 𝑐
 Where M is the gradient (change in y over the change in x), and c is the position above or
below the x axis.
 The gradient M, is the change in y over the change in x.
(such that 𝑀 =
Δ𝑦
Δ𝑥
=
𝑦1−𝑦2
𝑥1−𝑥2
).
Example 1: Calculate the gradient between points A(3,6) and B(4, 9).
 Solution: M(AB)=
𝑌𝐴−𝑌𝐵
𝑥𝐴−𝑥𝐵
=
6−9
3−4
=
−3
−1
= 3.

6. POSITIVE OR
NEGATIVE
GRADIENT.
 Since the above example
has a positive gradient, this
means that the graph will
be increasing from -
∞ 𝑡𝑜 ∞.
 If the gradient was
negative, therefore the
graph will be decreasing
from -∞ 𝑡𝑜 ∞. The graph
will look like this:

7. Gradient,
continued…
 https://www.youtube.com
/watch?v=T3n74ul5-o8
 https://www.youtube.com
/watch?v=MYCH7gswI4k
 https://www.mashupmath
.com/blog/finding-slope-
of-a-line-rise-over-run

8. The effect of “c”
 The value of affects the graph
when it cuts the y axis. This is
also known the y intercept of the
graph.
 Therefore, if c>0, the graph shift
vertically upwards.
 And if c<0, the graph shifts
vertically downwards.
M<0
C>0
C<0
M>0

10. The intercepts of a straight
line graph.
 The intercepts of a graph are points that cuts either the y axis or the x axis that
lies on the graph.
 The x- and y-intercepts are used in sketching linear functions. Because we only
need two points to graph a line, the intercepts are all we require and the
simplest coordinates to get. To obtain the two points, we will set the values of x
and y to 0 (Geraldine, 2021).
 To calculate the x intercept, let the y value be equated to zero.
 Example 2: 𝑦 = 3𝑥 − 1. let y=0
0 = 3𝑥 − 1
1 = 3𝑥
𝑥 =
1
3
.
The graph cuts at (
1
3
, 0) on the x axis.
 To calculate the y intercept, let the x value be equated to zero. Therefore, in this
case, we substitute the variable x with zero.
𝑦 = 3𝑥 − 1
= 3 0 − 1
= −1
The graph cuts at (0, -1) on the y axis.

11. Domain and Range
 DOMAIN: this is where the x values are defined in the straight
line graph.
 RANGE: this is where the y values are defined in a straight
line graph.
 The domain for a straight line graph ( y=mx+c) is {𝑥: 𝑥 ∈ 𝑅}
because there is no value of x for which y is undefined.
 The range of the straight line graph (y=mx+c) is {y: 𝑦 ∈ 𝑅}
because y can take on any real value/number.

12. Reference List
1. Barek, N. (2013). Topic 1: Section 1.1 –Graphs of linear equations. Available from Slideshare at
https://www.slideshare.net/nahomyitbarek/topic1-16365779?qid=bf814970-084d-4a05-
a611-e98f6bd2dfad&v=&b=&from_search=10 [accessed on 21 August 2022].
2. Estelav, (2013). Linear Functions. Available from Slideshare at
https://www.slideshare.net/estelav/linear-functions-20097351?qid=9219ab42-b21c-4238-
bd52-b3ec7a683dc6&v=&b=&from_search=4 [Accessed on 21 August 2022].
3. Geraldine, M. (2021). Graph of linear function. Available from Slideshare at
https://www.slideshare.net/MartinGeraldine/graph-of-linear-function [Accessed on 20 August
2022].
4. MacLane, S., (2012). Mathematics form and function. Springer Science & Business Media.
5. Mushipe, M. and Ogbonnaya, U. I., (2019). Geogebra and Grade 9 learners’ achievement in linear
functions.
6. Racso, E. (2014). AS LEVEL Function (CIE) EXPLAINED WITH EXAMPLE AND DIAGRAMS.
Available from Slideshare at https://www.slideshare.net/RACSOstudentHELP/function-
edited?qid=20b4981c-afc2-4e55-a270-340a9f5c616f&v=&b=&from_search=10 [accessed on 20
August 2022].
7. Teacher Andoo, (2012). Linear functions 1. Available from Slideshare at
https://www.slideshare.net/teacherandoo/linear-functions-1?qid=7eb23bb1-4f42-42cf-ab16-
abe868bbf7af&v=&b=&from_search=2 [Accessed on 21 August 2022].
8. Volunteers, Siyavula Grade 10 Mathematics. Department of Basic Education. South Africa.