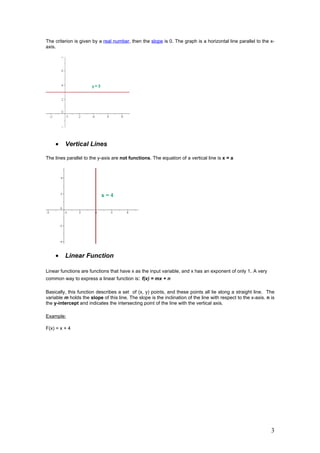
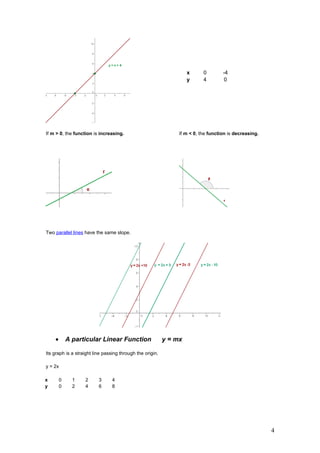
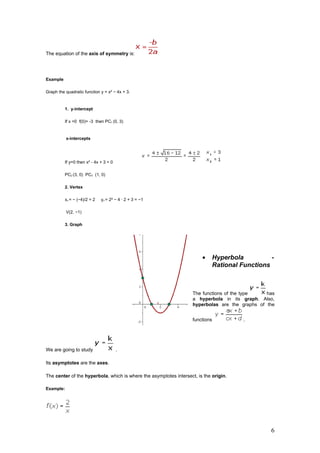
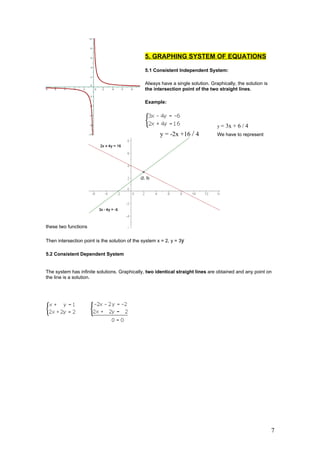
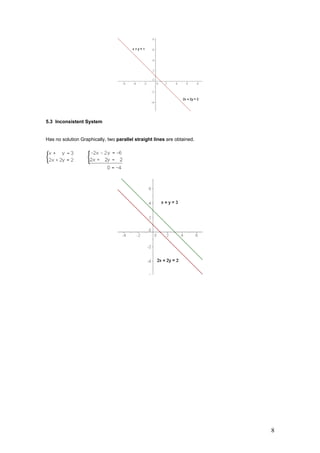
The document discusses various functions including: 1. Coordinate planes and plotting points. 2. Linear functions defined as f(x)=mx+b and their properties like slope and intercepts. 3. Quadratic functions defined as f(x)=ax^2+bx+c and their properties like intercepts, vertex, and parabolic graph shape. 3. Systems of equations and their graphical representations as either a single intersection point, identical overlapping lines, or parallel non-intersecting lines depending on if the systems are consistent/dependent or inconsistent.

1. I.E.S. MARÍA BELLIDO - BAILÉN
BILINGUAL SECTION – MARÍA ESTHER DE LA ROSA
FUNCTIONS
1. COORDINATES IN THE PLANE
To represent points in the plane, two perpendicular straight lines are used. They are called the Cartesian
axes or coordinate axes. The horizontal axis is called the x-axis. The vertical axis is called the y-axis.
Point O, where the two axes intersect is called the origin O, it has coordinates (0,0).
The coordinates of a point, P, are represented by (x, y).
The points that are on the vertical axis have their The points that are on the horizontal axis have
abscissa equal to 0. their ordinate equal to 0.
Example: Plot the following points
A(1, 4), B(-3, 2), C(0, 5), D(-4, -4), E(-5, 0), F(4, -3), G(4, 0), H(0, -2)
1

2. 2. FUNCTION
A real function of real variables is any function, f, that associates to each element of a certain subset
(domain), another real number (image).
f:D
x f(x) = y
The number x is called the independent variable. The number, y, associated for f to the of value x, is
called the dependent variable. The image of x is designated by f(x):
3. TABLE OF VALUES OF A FUNCTION
If f is a real function, every pair (x, y) determined by the function f corresponds to the Cartesian plane as
a single point P(x, y) = P(x, f(x)).
The set of points belonging to a function is unlimited and the pairs are arranged in a table of values which
correspond to the points of the function. These values, on the Cartesian plane, determine points on the
graph. Joining these points with a continuous line gives the graphical representation of the function.
Example: f(x)= 5x -3
f(1)= 5 1 – 3 = 2 f(-1) = 5 (-1) – 3 = -8 f(0)= 5 0 – 3 = -3
x y
1 2
-1 -8
4. TYPES OF FUNCTIONS
• Constant Functions
0 -3
The equation of a constant function is y = b
2

3. The criterion is given by a real number, then the slope is 0. The graph is a horizontal line parallel to the x-
axis.
• Vertical Lines
The lines parallel to the y-axis are not functions. The equation of a vertical line is x = a
• Linear Function
Linear functions are functions that have x as the input variable, and x has an exponent of only 1. A very
common way to express a linear function is: f(x) = mx + n
Basically, this function describes a set of (x, y) points, and these points all lie along a straight line. The
variable m holds the slope of this line. The slope is the inclination of the line with respect to the x-axis. n is
the y-intercept and indicates the intersecting point of the line with the vertical axis.
Example:
F(x) = x + 4
3

4. x 0 -4
y 4 0
If m > 0, the function is increasing. If m < 0, the function is decreasing.
Two parallel lines have the same slope.
• A particular Linear Function y = mx
Its graph is a straight line passing through the origin.
y = 2x
x 0 1 2 3 4
y 0 2 4 6 8
4

5. • Identity Function y = x
Its graph is the bisector of the first and third quadrant.
• Quadratic Function
The equation of a quadratic function is y = ax² + bx +c. Its graph is a parabola.
A parabola can be built from these points:
1. y-intercepts and x-intercepts
1. For the intercept with the y-axis, the first coordinate is always zero:
If x=0 then f(0) = a · 0² + b · 0 + c = c (0, c)
2. For the intercept with the x-axis, the second coordinate is always zero:
If y=0 ax² + bx +c = 0 We must solve the resultant quadratic equation:
2. Vertex
The axis of symmetry passes through the vertex of the parabola.
5

6. The equation of the axis of symmetry is:
Example
Graph the quadratic function y = x² − 4x + 3.
1. y-intercept
If x =0 f(0)= -3 then PC1 (0, 3)
x-intercepts
If y=0 then x² - 4x + 3 = 0
PC2 (3, 0) PC3 (1, 0)
2. Vertex
xv = − (−4)/2 = 2 yv = 2² − 4 · 2 + 3 = −1
V(2, −1)
3. Graph
• Hyperbola -
Rational Functions
The functions of the type has
a hyperbola in its graph. Also,
hyperbolas are the graphs of the
functions .
We are going to study .
Its asymptotes are the axes.
The center of the hyperbola, which is where the asymptotes intersect, is the origin.
Example:
6

7. 5. GRAPHING SYSTEM OF EQUATIONS
5.1 Consistent Independent System:
Always have a single solution. Graphically, the solution is
the intersection point of the two straight lines.
Example:
y= 3x + 6 / 4
y = -2x +16 / 4 We have to represent
these two functions
Then intersection point is the solution of the system x = 2, y = 3y
5.2 Consistent Dependent System
The system has infinite solutions. Graphically, two identical straight lines are obtained and any point on
the line is a solution.
7

8. 5.3 Inconsistent System
Has no solution Graphically, two parallel straight lines are obtained.
8