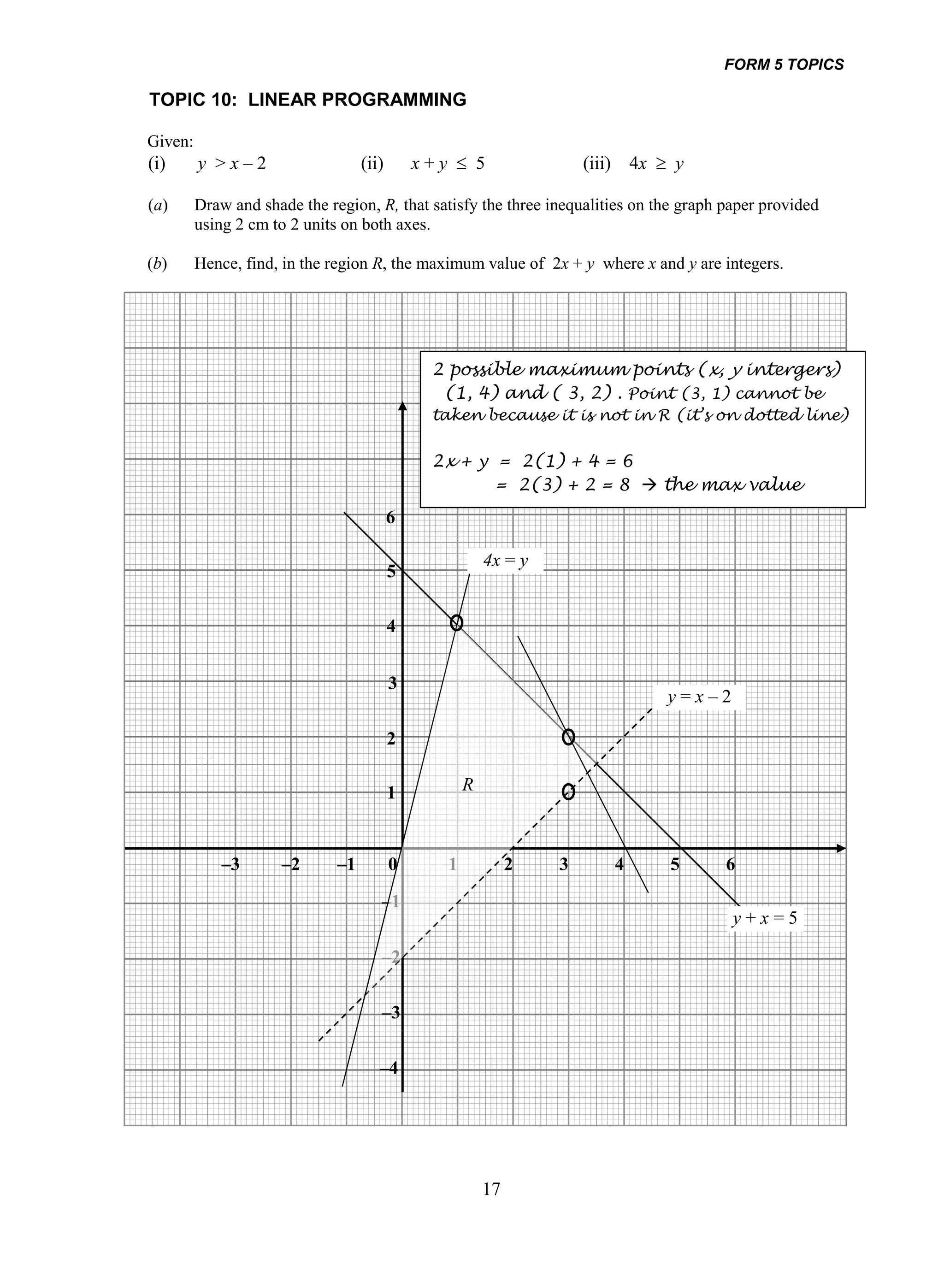
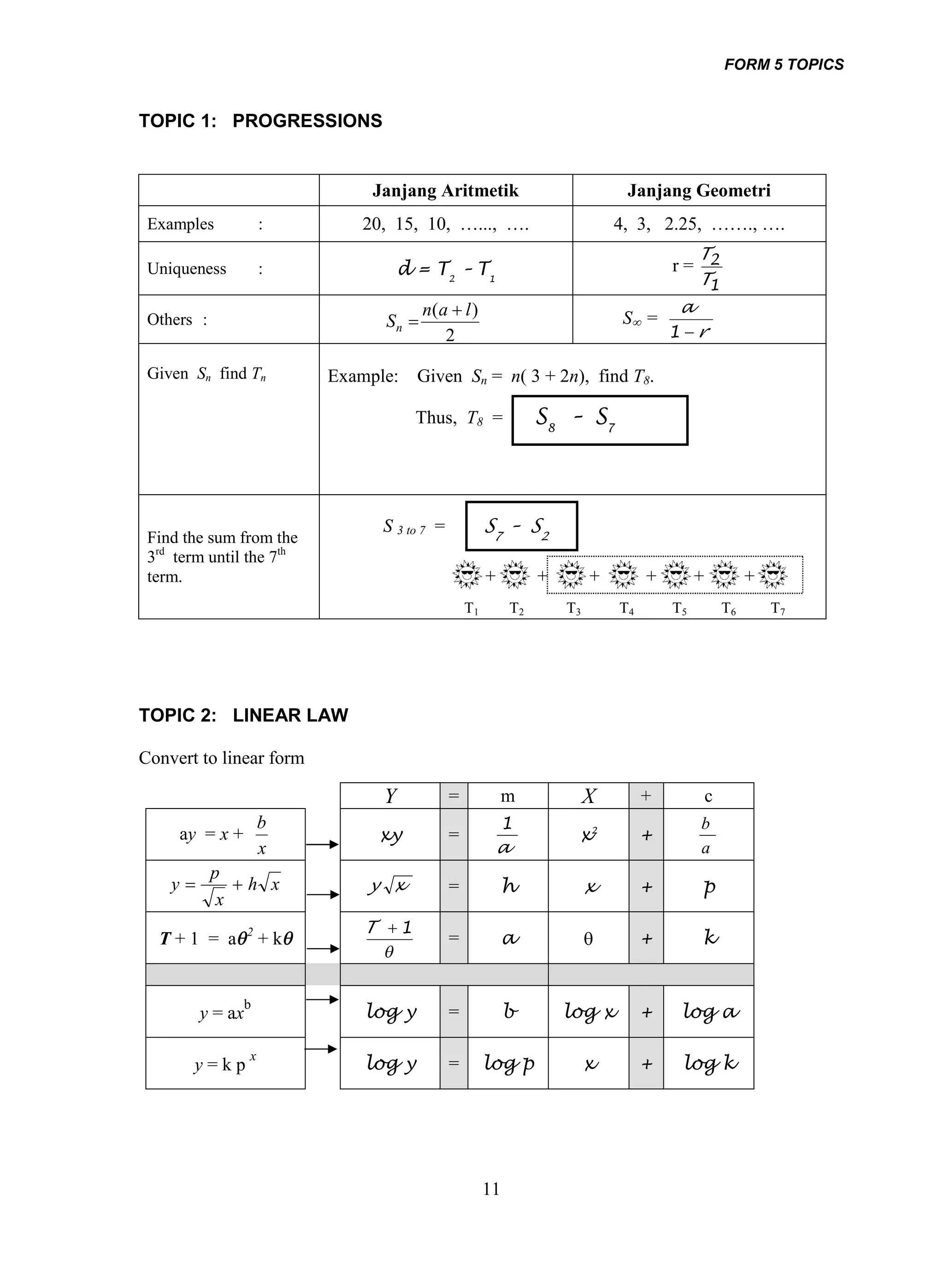
1. The document provides an overview of important topics covered in Form 4 and Form 5 mathematics. These include functions, quadratic equations, trigonometry, statistics, calculus, and coordinate geometry. 2. Examples of how to solve different types of problems are given for each topic, such as finding the sum and product of roots for quadratic equations or using rules of logarithms to simplify logarithmic expressions. 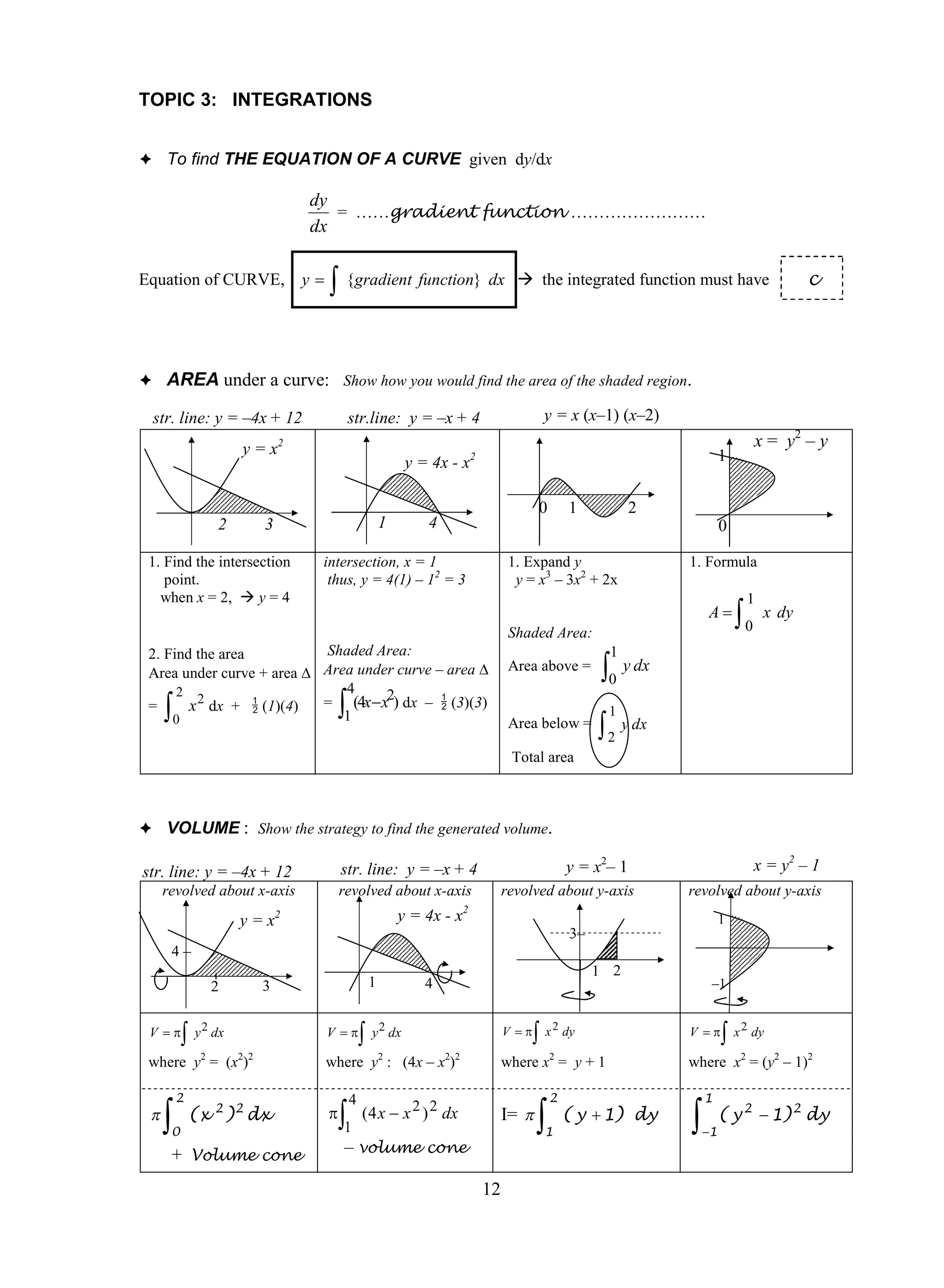3. Strategies for solving problems involving concepts like differentiation, integration, progressions, and linear laws are outlined. Methods for finding volumes or areas under curves are also summarized briefly.

1. FORMAT&COMPONENT
TO EXCELL in
You need to…
 set TARGET
 familiar with FORMAT of PAPER
 do EXERCISES
Exercise Exercise Exercise Exercise Exercise
Exercise Exercise Exercise Exercise Exercise
Exercise Exercise Exercise Exercise Exercise
Exercise Exercise Exercise Exercise Exercise
Exercise Exercise Exercise Exercise Exercise
Exercise Exercise Exercise Exercise Exercise
Exercise Exercise Exercise Exercise Exercise
Exercise Exercise Exercise Exercise Exercise
Exercise Exercise Exercise Exercise Exercise
Exercise Exercise Exercise Exercise Exercise
Exercis e Exercis e Exercis e Exercis e Exercis e
My TARGET
1

2. PAPER 1 (3472 / 1)
No Items Comments
1 No. of questions 25 questions (Answer ALL)
2 Total Marks
……80 marks………….
3 Time
…….2 hours
4 Level of difficulty Low : Moderate : High
6 : 3 : 1
PAPER 2 (3472 / 2)
No Items Comments
1 Three sections Section A Section B Section C
2 No of questions 6 5 4
Answer Choose Choose
(need to answer 12
questions )
…ALL….. …four…. …two…..
3 Total marks (100) 40 marks 40 marks 20 marks
4 Time
………2 ½ hours……………..
Low : Moderate : High
5 Level of difficulty 4 3 3
2

3. FORMAT&COMPONENT
1 mark  1.5 minutes
Check answers
* Extra Time = ………………………………….
1. Functions
2. Quadratic Equations
3. Quadratic Functions
ALGEBRA 4. Indices & Logarithms
5. Simultaneous Equations
6. Progressions
7. Linear Law
1. Coordinate Geometry
Geometry 2. Vector
1. Differentiation
Calculus 2. Integration
1. Circular Measures
Triginometry 2. Trigonometric Functions
1. Statistics
2. Probability
STATISTICS
3. Permutation & Combination
4. Distribution Probability
1. Index Numbers
Social Science
2. Linear Programming
1. Solutions to Triangle
Science & Technology
2. Motion in a Straight Line.
3

4. FORM 4 TOPICS
P(X)
Learn with your heart
and you’ll see the wonders …
4

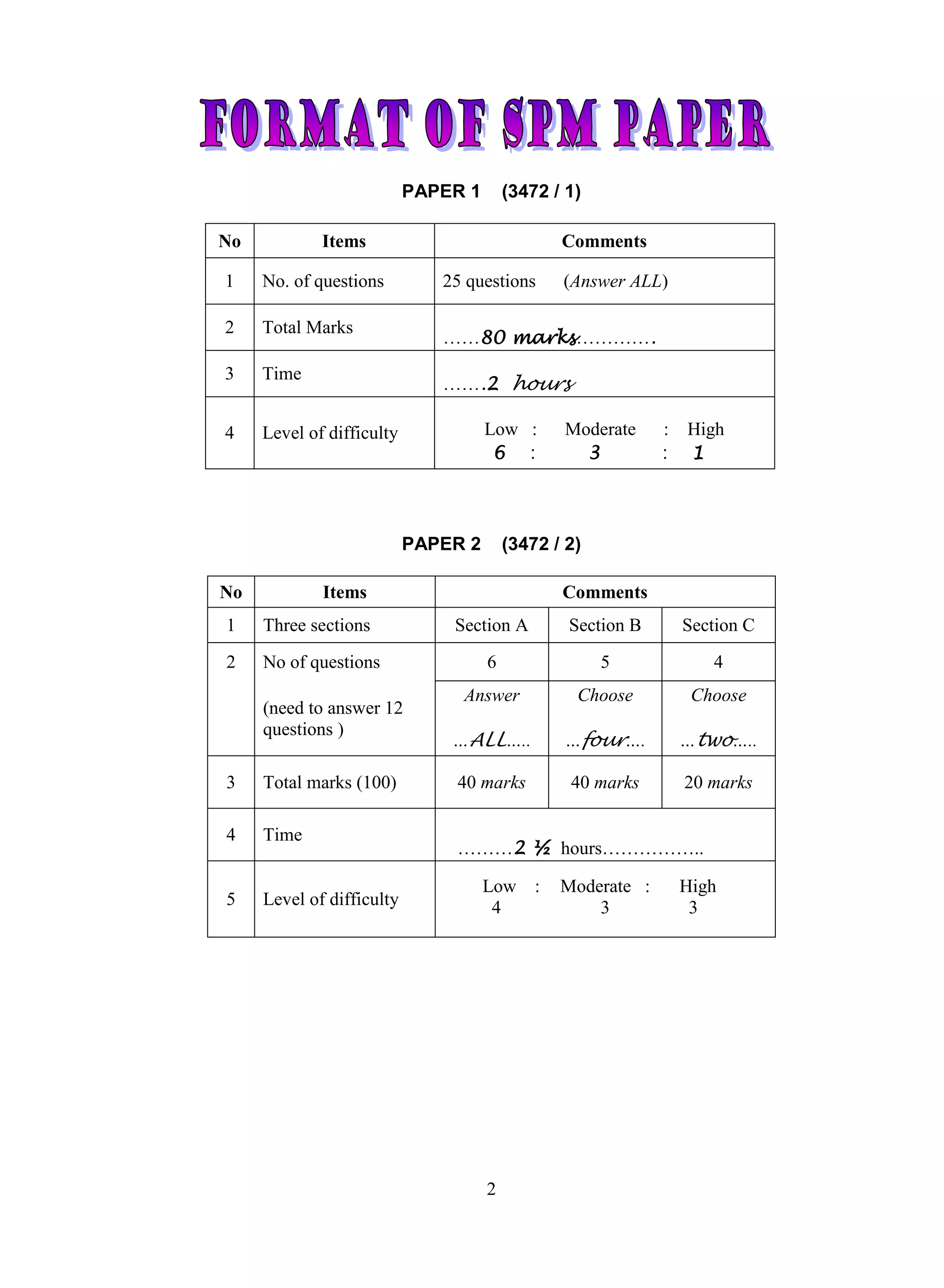
5. FORM 4 TOPICS
TOPIC 1 : FUNCTIONS
a b
 f(a) = b  object = …………………….. image = ………………..
-1
 Given f (x) and gf(x). Find g(x) .  Thus, g(x) = gf f
3x  5
 f ( x)  , X1
x 1
TOPIC 2: QUADRATIC EQUATIONS [ ax2 + bx + c = 0 ]
Types of roots
- two distinct real roots
>0 - intersects at two points
0 Real roots
- two equal roots
b2 – 4ac =0 - touches / tangent
<0 - no root
- does not intersect
- f(x) is always positive
Sum and Product of Roots [ ax2 + bx + c = 0 ]
b c
Sum of roots, ( + ) = Product of roots ( ) = x2 – Sx + P =0
a a
TOPIC 3: QUADRATIC FUNCTIONS
1. General form CTS form
f (x) = ax2 + bx + c = a( x + p)2 + q
Similarity Same value of a Same value of a
c = y-intercept. q = max/min value
Difference
of f(x)
Able to find: Able to find
Specialty - shape - turning point
- y intercept ( - p , q)
5

6. FORM 4 TOPICS
2. Sketch Graphs: y = ax2 + bx + c
(a) From the graph
i value of a : Positive
ii value of b2-4ac: <0
iii type of roots : No roots
iii y-intercept : C
Equation of axis of b
iv X= 
symmetry : 2a
3. Inequalities : Solving 2 inequalities  use Graph
(x – a) (x – b) > 0 (x – c) (x – d) < 0
1. Let the right hand side = 0
- factorise
2. Find the roots of the equation
3. Sketch the graph
3. Determine the region  c d
positive or negative a b
x<a , x > b, c<x<d
………………………. …………….………
TOPIC 4: SIMULTANEOUS EQUATIONS
Substitution
 Use ……………………………….. method
intersection
 To find the ………………………………… points between a straight line and a curve.
6

7. FORM 4 TOPICS
TOPIC 5: INDICES & LOGARITHM
Change the base to
x+1 x 1
Use Index rule : (i) 5 . 125 = the same number
……………………….
25
5x +1. 5 3x = 5–2
x + 1 + 3x = – 2
x = –
INDEX
Insert log on both
sides
Use log : (ii) 8  3x = 7 ............................ IND
n+1 n Steps of solutions
Use substitution : (iii) 3 + 3 = 12
or can be factorise 3 . 3 + 3n = 12
n
a(3) + a = 12 1. separate the index
4a = 12
a = 3 2. substitute
n
3 =3  n=1
2n n
(iv) 3 + 5. 3 = 6
a2 + 5a – 6 = 0
(a – 1) (a + 6) = 0
a = 1 , a = –6
3n = 1 3n  –6
 n=0
LOGARITHM : Use Rules of logarithms to simplify or to solve logarithmic equations
log2 (x + 9) = 3 + 2 log2 x
log2 (x + 9) – log2 x 2
=3
log2 (x + 9) =3
x2
x + 9 = 23
x2
x + 9 = 8x 2
8x2 – x – 9 = 0
(8x -9) (x + 1) = 0
x –1, x= 
7

8. FORM 4 TOPICS
TOPIC 6: COORDINATE GEOMETRY
 Distance   Ratio theorem 
 Mid point   Equation of straight line y = mx + c
Arrange
 Area (positive) : general form ax + by + c = 0
anticlockwise
 Gradient : gradient form y = mx + c
- parallel m1 = m2 x y
: intercept form  1
- perpendicular m1 m2 = –1 a b
Equation of locus : …use distance formula………………….
Rhombus : ……its diagonal are perpendicular to each other ……….
Parallelogram, square, rectangle, rhombus. its diagonal share the same mid point
TOPIC 7: STATISTCS
EFFECT ON CHANGES TO DATA
The change in
Interquartile
values when Mean Mode Median Range range  Variance
each data is
Added with k +k +k +k unchange unchange unchange unchange
Multiplied by m m m m m m m m 2
TOPIC 8: CIRCULAR MEASURES
 
…… radian = ……… 
180
 For s = r and A = ½ r2 , the value of  is in ……radian…….

Area of segment = ½ r2 (  - sin )

 Shaded angle =  –
 rad
8

9. FORM 4 TOPICS
TOPIC 9: DIFFERENTIATION
gradient of normal mN mT = –1
gradient of tangent
dy equation of normal
Tangent mT =
dx
equation of tangent y – y1 = m(x – x1)
Rate of change dy = dy  dx
dt dx dt
Applications
 y = dy   x
Small Changes approximate value
dx
y ORIGINAL + y
d2y
minimum  0
dx 2
Turning points
dy maximum d2y
dx = 0  0
dx 2
TOPIC 10: SOLUTION OF TRIANGLES
 Sine Rule
- Ambiguous Case  two possible angles  acute and obtuse angle
 Cosine Rule
 Area =  ab sin C
TOPIC 11: INDEX NUMBERS
 I A, B  I B, C = I A, C
 Given that the price index of an item is 120. If the price index increases at the same
rate in the next year, what will be the new price index of the item?
120
………………………………120  ……………………………………………
100
……………………………………………………………………………………….
9

10. :
10

11. FORM 5 TOPICS
TOPIC 1: PROGRESSIONS
Janjang Aritmetik Janjang Geometri
Examples : 20, 15, 10, …..., …. 4, 3, 2.25, ……., ….
T
Uniqueness : d = T2 – T1 r= 2
T1
n( a  l ) a
Others : Sn  S =
2 1 r
Given Sn find Tn Example: Given Sn = n( 3 + 2n), find T8.
Thus, T8 = S8 – S7
S 3 to 7 = S7 – S2
Find the sum from the
3rd term until the 7th
term. + + + + + +
T1 T2 T3 T4 T5 T6 T7
TOPIC 2: LINEAR LAW
Convert to linear form
Y = m X + c
b 1 b
ay = x + xy = x2 +
x a a
p
y h x y x = h x + p
x
T 1
T + 1 = a 2 + k = a  + k

b
y = ax log y = b log x + log a
x
y=kp log y = log p x + log k
11

12. TOPIC 3: INTEGRATIONS
 To find THE EQUATION OF A CURVE given dy/dx
dy
= ……gradient function ……………………
dx
Equation of CURVE, y  {gradient function} dx  the integrated function must have c
 AREA under a curve: Show how you would find the area of the shaded region.
str. line: y = –4x + 12 str.line: y = –x + 4 y = x (x–1) (x–2)
y = x2 x = y2 – y
y = 4x - x2 1
0 1 2
2 3 1 4 0
1. Find the intersection intersection, x = 1 1. Expand y 1. Formula
point. thus, y = 4(1) – 12 = 3 y = x3 – 3x2 + 2x
when x = 2,  y = 4 1
Shaded Area:
A 0 x dy
Shaded Area: 1
0 y dx
2. Find the area
Area under curve + area  Area under curve – area  Area above =
4

2 2

2
= x dx +  (1)(4) = (4xx ) dx –  (3)(3) 1
 2 y dx
0 1 Area below =
Total area
 VOLUME : Show the strategy to find the generated volume.
str. line: y = –4x + 12 str. line: y = –x + 4 y = x2– 1 x = y2 – 1
revolved about x-axis revolved about x-axis revolved about y-axis revolved about y-axis
2
y=x 2 y = 4x - x 1
3–
4–
1 2
2 3 1 4 –1
y y x x
2 dx 2 dx V  2 dy 2 dy
V  V  V 
where y2 = (x2)2 where y2 : (4x – x2)2 where x2 = y + 1 where x2 = (y2 – 1)2
2 2 1
  
4

0
(x 2 ) 2 dx  1 (4 x  x 2 ) 2 dx I= 
1
( y  1) dy
1
( y 2  1) 2 dy
+ Volume cone – volume cone
12

13. FORM 5 TOPICS
TOPIC 4: VECTORS
 If vectors a and b are parallel, thus, ………a = k b …………………….………..
 If OA = a and OB = b , thus, AB = … OB - OA……= b – a ………………..….
 If T is the mid point of AB thus, OT = ……AB………………………………………...
 Given m = 2i + 3j and n = i – 4j find,
i) m+n = ……2i + 3j + ( i – 4j ) = 3i – j …………….
ii) m + n = …… 32  ( 1)2  10 …………………………………………..
1
iii) unit vector in the direction of m + n = …… (3i  j ) ………………………
10
1    2   2  1    3
 If A(1, 3) and B(–2, 5) find AB : …OA =   , OB = 
3 
      
 5   AB =  5  – 3  =  2 
         
can also be written in the form of i and j.
 Given CD = 2h x + 5y and CD = 8x – 2hky , find the value of h and of k.
2h x + 5y = 8x – 2hky ……………………… (comparison method)
compare coef. of x , compare coef of y.
TOPIC 5 : TRIGONOMETRIC FUNCTIONS
 Solving equation : SIMPLE
Solve: 2 cos 2x = 3 for 0  x  360
1. Separate coefficient of trigo 3
cos 2x = positive values
2
2. Determine the quadrant  1st and 4th
quadrant
3. Find the reference angle 2x = 30
4. Find new range (if necessary). 0  x  720
2x = 30, 330, 390, 690
5. Find all the angles
x = 15, 165, 195, 345
13

14.  Solving Equation : Using Identity WHEN?
sin 2x cos x = sin x
cos 2x cos x = 0 ………Angles are not the same………
sin2 x + 3cos x = 3
2 sec2 x + tan2 x = 5 ………have different functions ……….
 Proofing: Use Identity
sinA 1 . 1 1
Remember : tanA  
, tan  , sec 2x = , cosec A =
cosA cot cos 2x sin A
 Use of Trigo Ratios: Examples:
From the question given, If sin A =  , A is not acute,
1. Determine the quadrant involved. ……second……………….
2. Determine the values of the other trig. fxn cos and tan = negative
in the quadrant. cos A =  3 , tan A = – 
5
find sin 2A
3. Do you need to use identity? sin 2A = 2 sin A cos A
4. Substitute values = 2 ( ) (  3 )
5
= 24

25
 Sketch Graphs
y = a sin b x + c a = max / minimum point
a cos b x + c
a tan b x + c b = number of basic shape between 0 and 2
c = increase / decrease translation of the
Basic Graphs
y = sin x y = cos x y = tan x
1- 1-
2 2 2
–1- –1-
14

15. FORM 5 TOPICS
TOPIC 6: PERMUTATIONS & COMBINATIONS
Permutations = …order of arrangement is important Combinations =…order not important….
Three committee members of a society are to be Three committee members of a society are to be
chosen from 6 students for the position of chosen from 6 students. Find the number of
president, vice president and secretary. Find ways the committee can be chosen.
the number of ways the committee can be
chosen.
Permutations: 6 3 P Combination: 6 3C
with condition:
Find the number of different ways the letters Find the number of ways 11 main players of a
H O N E S T can be arranged if it must football team can be chosen from 15 local
begin with a vowel. players and 3 imported players on the
2 5 4 3 2 1 condition that not more than 2 imported
players are allowed.
condition  2 Import.
condition Case : (2 Import, 9 local) or 3C2. 15C9
vowels = 2 choices 3 15
(1 import 10 locals) or + C1. C10
3 15
( 0 import 11 locals) + C0. C11
TOPIC 7: PROBABILITY
n ( A)
 P(A) =
n ( S)
- Probability event A or B occurs = P(A) + P(B)
- Probability event C and D occurs = P(A) . P(B)
 Considering several cases:
Probability getting the same colors = Example: (Red and Red) or (Blue and blue)
Probability of at least one win in two matches = (win and lose) or (lose and win) or (win and win)
Or using compliment event = 1 – (lose and lose)
15

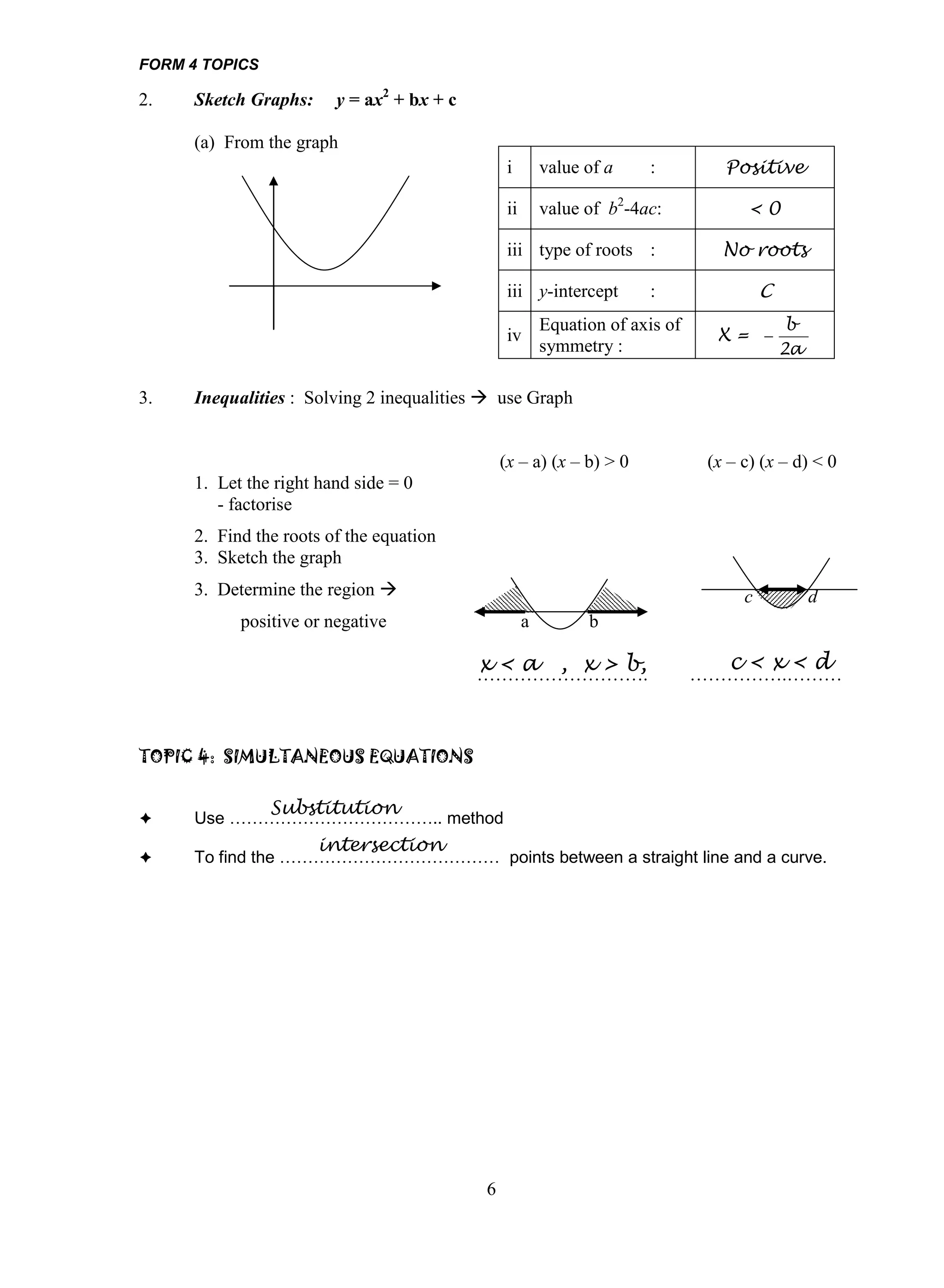
16. TOPIC 8: PROBABILITY DISTRIBUTION
P(X)
BINOMIAL DISTRIBUTION _
0.3
0.25 _
- The table shows the binomial probability distribution of
0.2 _
an event with n = 4 .
0.15 _
0.1 _
X=r r=0 r=1 r=2 r=3 r=4
0.05 _
P(X) 0.2 0.15 0.3 0.25 0.1 0 1 2 3 4 X=r
Graph of Binomial Prob Distribution
total = 1
- formula: P(X = r) = n C r p r q n – r
- mean,  = np standard deviation = npq variance = npq
NORMAL DISTRIBUTION
X 
- Formula : Z 

- Type 1 : Given value of X  find the value of Z  find the probability
[use formula] [use calculator]
- Type 2 : Given the probability Find the value of Z  Find its value of X .
[use log book] [use formula]
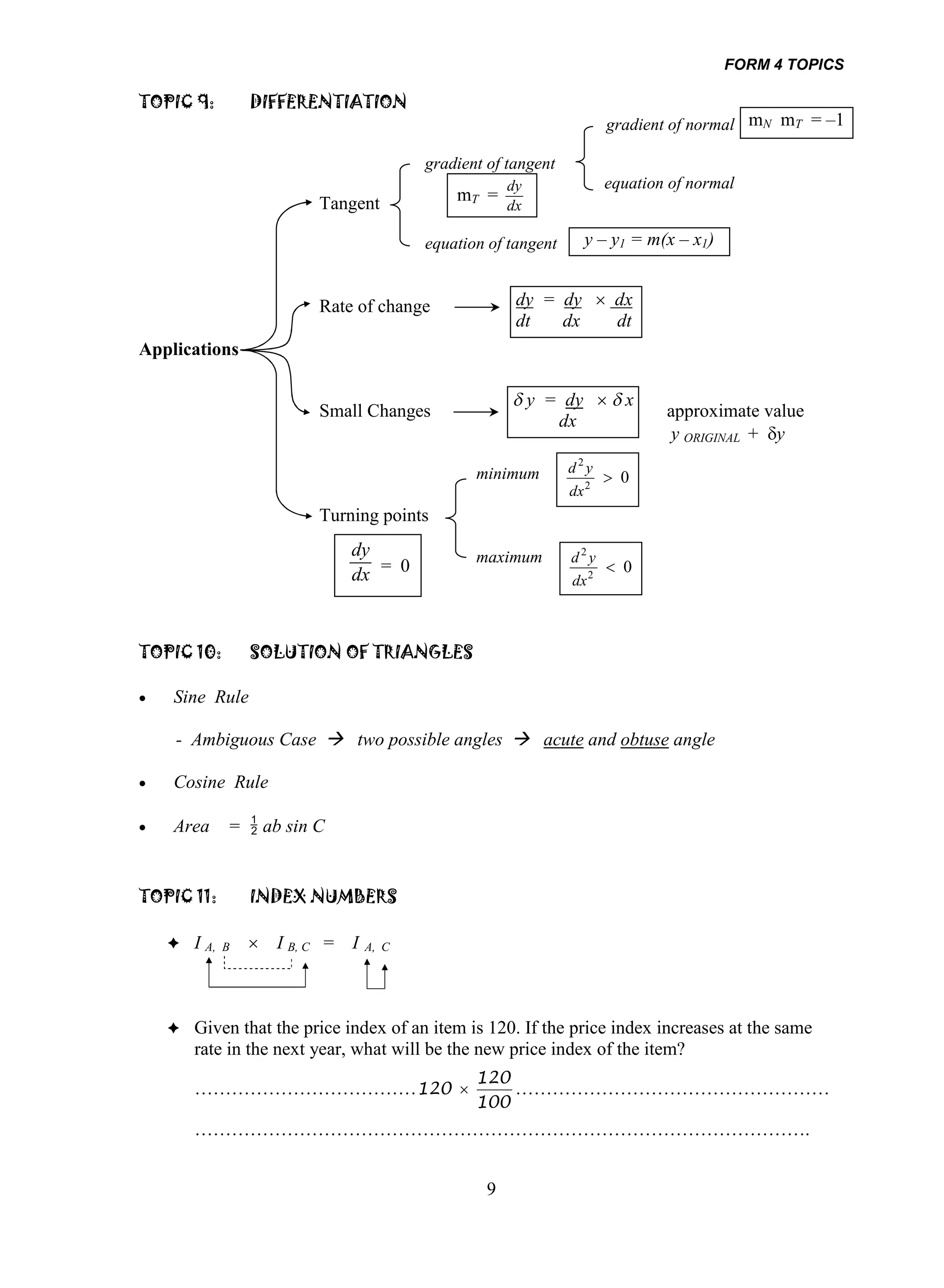
TOPIC 9: MOTION IN STRAIGHT LINES
Displacement, s Velocity, v Acceleration, a

ds dv d 2s
s= v dt v a =
dt dt dt 2
dv
Maximum velocity - 0 a=0
dt
return to O s=0 - -
stops momentarily v=0
da
max. acceleration 0
dt
16

17. FORM 5 TOPICS
TOPIC 10: LINEAR PROGRAMMING
Given:
(i) y >x–2 (ii) x+y  5 (iii) 4x  y
(a) Draw and shade the region, R, that satisfy the three inequalities on the graph paper provided
using 2 cm to 2 units on both axes.
(b) Hence, find, in the region R, the maximum value of 2x + y where x and y are integers.
2 possible maximum points (x, y intergers)
(1, 4) and ( 3, 2) . Point (3, 1) cannot be
taken because it is not in R (it’s on dotted line)
2x + y = 2(1) + 4 = 6
= 2(3) + 2 = 8  the max value
6
4x = y
5
4
3
y=x–2
2
1 R
–3 –2 –1 0 1 2 3 4 5 6
–1
y+x=5
–2
–3
–4
17