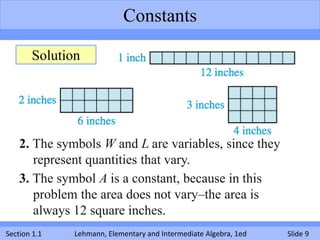
The document introduces key concepts in algebra including variables, constants, types of numbers (counting, integers, rational, irrational, real), graphs, averages, and positive and negative numbers. It provides examples and guidelines for understanding these concepts. Variables represent quantities that can vary, while constants represent fixed values. Different number sets are explained and visualized on a number line. Averages are calculated by adding values and dividing by the total count. Positive numbers are greater than zero, while negative numbers are less than zero.

1. Chapter 1
Introduction to
Modeling

2. Section 1.1
Variables and Constants

3. Variables
Definition
A variable is a symbol which represents a quantity that can
vary.
For example, we can define h to be the height (in feet)
of a specific child. Height is a quantity that varies: As
time passes, the child’s height will increase. So, h is a
variable. When we say h = 4, we mean that the child’s
height is 4 feet.
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 3

4. Variables
Example 1
1. Let s be a car’s speed (in miles per hour). What is
the meaning of s = 60?
2. Let n be the number of people (in millions) who
work from home at least once a week during
normal business hours. For the year 2005, n = 21.
What does that mean in this situation?
3. Let t be the number of years since 2005. What is
the meaning of t = 4?
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 4

5. Variables
Solution
1. Let s be a car’s speed (in miles per hour). What is
the meaning of s = 60?
The speed of the car is 60 miles per hour.
2. Let n be the number of people (in millions) who
work from home at least once a week during
normal business hours. For the year 2005, n = 21.
What does that mean in this situation?
In 2005, 21 million people worked from home at
least once a week during normal business hours.
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 5

6. Variables
Solution
3. Let t be the number of years since 2005. What is
the meaning of t = 4?
2005 + 4 = 2009; so, t = 4 represents the year 2009.
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 6

7. Constants
Definition
A constant is a symbol which represents a specific
number (a quantity that does not vary).
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 7

8. Constants
Example 3
A rectangle has an area of 12 square inches. Let W
be the width (in inches), L be the length (in inches),
and A be the area (in square inches).
1. Sketch three possible rectangles of area 12
square inches.
2. Which of the symbols W, L, and A are variables?
Explain.
3. Which of the symbols W, L, and A are constants?
Explain.
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 8

9. Constants
Solution
2. The symbols W and L are variables, since they
represent quantities that vary.
3. The symbol A is a constant, because in this
problem the area does not vary–the area is
always 12 square inches.
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 9

10. Counting Numbers
Definition
The counting numbers, or natural numbers, are the
numbers
1, 2, 3, 4, 5, ...
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 10

11. Integers
Definition
The integers are the numbers
..., −3, −2, −1, 0, 1, 2, 3, ...
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 11

12. The Number Line
We can visualize numbers on a number line.
Each point (location) on the number line represents
a number. The numbers increase from left to right.
We refer to the distance between two consecutive
integers on the number line as 1 unit.
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 12

13. Rational Numbers
Definition
The rational numbers are the numbers that can be
n
written in the form , where n and d are integers
and d is nonzero. d
Examples
3 2 4
4
7 5 1
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 13

14. Irrational Numbers
Definition
An irrational number can NOT be written in the
n
form , where n and d are integers and d is
d
nonzero.
Examples
 3 5
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 14

15. Decimals
A rational number can be written as a decimal
number that either terminates or repeats:
An irrational number can be written as a decimal
number that neither terminates nor repeats. It is
impossible to write all the digits of an irrational
number, but we can approximate the number by
rounding:   3.14
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 15

16. Real Numbers
Definition
The real numbers are all of the numbers
represented on the number line.
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 16

17. Real Numbers
Every counting number is an integer, every integer
is a rational number, and every rational number is a
real number. Irrational numbers are the real
numbers that are not rational.
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 17

18. Data
Definition
Data are values of quantities that describe authentic
situations.
We often can get a better sense of data by graphing
than by just looking at the data values.
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 18

19. Graphing Data
Example 7
Over the course of a semester, a student takes five
quizzes. Here are the points he earned on the quizzes,
in chronological order: 0, 4, 7, 9, 10. Let q be the
number of points earned by the student on a quiz.
1. Graph the student’s scores on a number line.
2. Did the quiz scores increase, decrease, stay
approximately constant, or none of these?
3. Did the increases in the quiz scores increase, decrease,
stay approximately constant, or none of these?
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 19

20. Graphing Data
Solution
1. We sketch a number line and write “q” to the right of
the number line and the units “Points” underneath
the number line. Then we graph the numbers 0, 4, 7,
9, and 10.
2. From the opening paragraph, we know that the quiz
scores increased.(From the graph alone, we cannot tell
that the quiz scores increased, because the order of the
quizzes is not indicated.)
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 20

21. Graphing Data
Solution
3. As we look from left to right at the points plotted on
the graph, we see that the distance between adjacent
points decreases. This means that the increases in the
quiz scores decreased. That is, the jump from 0 to 4
is greater than the jump from 4 to 7, and so on.
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 21

22. Average, mean
Definition
To find the average (or mean) of a group of
numbers, we divide the sum of the numbers by the
number of numbers in the group.
To find the average of the quiz scores included in
Example 7, first add the scores:
0 + 4 + 7 + 9 + 10 = 30, then divide the total, 30,
by the number of quiz scores, 5: 30 ÷ 5 = 6 points.
So, the average quiz score is 6 points.
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 22

23. Positive and Negative Numbers
The negative numbers are the real numbers less
than 0, and the positive numbers are the real
numbers greater than 0.
3
Negative numbers: –13 , –5.2 ,  ,  2
4
3
Positive numbers: 13 , 5.2 , , 2
4
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 23

24. Positive and Negative Numbers
Example 9
A person bounces several checks and, as a result, is
charged service fees. If b is the balance (in dollars)
of the checking account, what value of b represents
the fact that the person owes $50? Graph the
number on a number line.
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 24

25. Positive and Negative Numbers
Solution
Since the person owes money, the value of b is
negative: b = −50. We graph −50 on a number line.
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 25

26. Describing a Concept or Procedure
Guidelines on Writing a Good Response
• Create an example that illustrates the concept or
outlines the procedure. Looking at examples or
exercises may jump-start you into creating your
own example.
• Using complete sentences and correct
terminology, describe the key ideas or steps of
your example. You can review the text for ideas,
but write your description in your own words.
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 26

27. Describing a Concept or Procedure
Guidelines on Writing a Good Response
• Describe also the concept or the procedure in
general without referring to your example. It
may help to reflect on several examples and what
they all have in common.
• In some cases, it will be helpful to point out the
similarities and the differences between the
concept or the procedure and other concepts or
procedures.
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 27

28. Describing a Concept or Procedure
Guidelines on Writing a Good Response
• Describe the benefits of knowing the concept or
the procedure.
• If you have described the steps in a procedure,
explain why it’s permissible to follow these
steps.
• Clarify any common misunderstandings about
the concept, or discuss how to avoid making
common mistakes when following the procedure.
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 28

29. Describing a Concept or Procedure
Example 10
Describe the meaning of variable.
Solution
Let t be the number of hours that a person works in
a department store. The symbol t is an example of a
variable, because the value of t can vary. In
general, a variable is a symbol that stands for an
amount that can vary. A symbol that stands for an
amount that does not vary is called a constant.
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 29

30. Describing a Concept or Procedure
Solution
There are many benefits to using variables. We can
use a variable to describe a quantity concisely;
using the earlier definition of t, we see that the
equation t = 8 means that a person works in a
department store for 8 hours. By using a variable,
we can also use smaller numbers to describe
various years. In defining a variable, it is important
to describe its units.
Section 1.1 Lehmann, Elementary and Intermediate Algebra, 1ed Slide 30