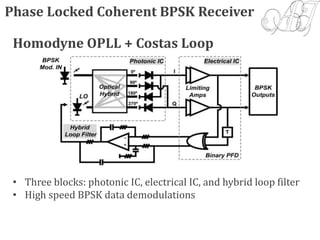
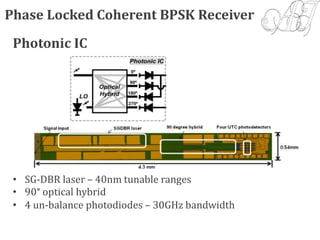
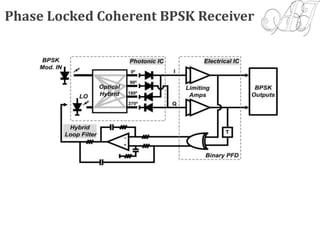
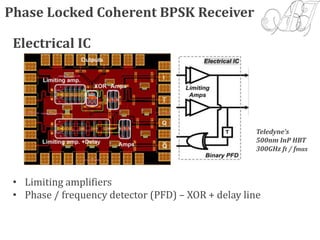
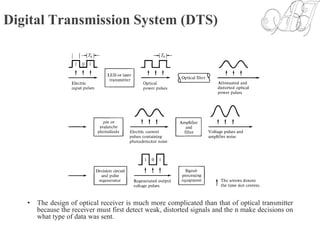
The document discusses digital transmission systems and coherent optical communications. It covers the following key points: 1) It describes the components and operation of optical receivers, including the challenges of detecting weak signals and making decisions on transmitted data. Error sources like intersymbol interference are also discussed. 2) Bit error rate and probability of error are defined, and formulas for calculating BER under Gaussian noise are provided. 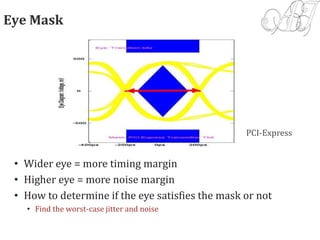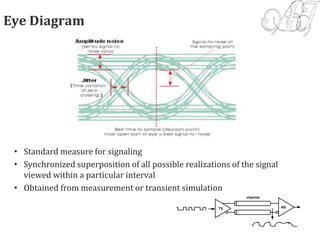3) Eye diagrams are introduced as a way to visualize signal quality over time. Factors like timing jitter and noise amplitude are described. 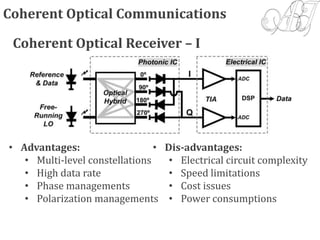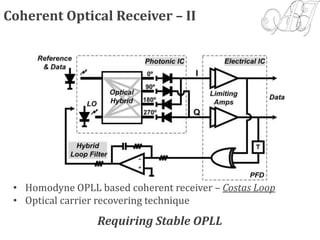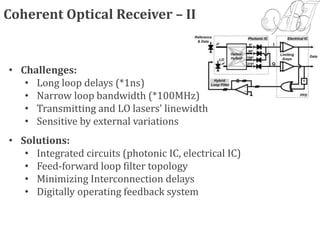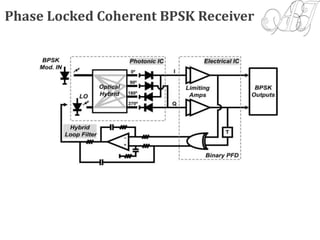4) Coherent optical receivers are overviewed, including their advantages for high data rates and constellations. Challenges in carrier recovery using optical phase-locked

1. UNIT-5
Mohammad Asif Iqbal
Assistant Professor,
Deptt of ECE,
JETGI, Barabanki

2. Digital Transmission System (DTS)
• The design of optical receiver is much more complicated than that of optical transmitter
because the receiver must first detect weak, distorted signals and the n make decisions on
what type of data was sent.

3. Error Sources in DTS
!
)(
)(
0
n
e
NnP
E
h
dttP
h
N
N
n
r


 





is the average number of electron-hole pairs in photodetector,
is the detector quantum efficiency and E is energy received in a time
interval and is photon energy, where is the probability
that n electrons are emitted in an interval .
N

 h )(nPr

[7-
1]
[7-2]

4. InterSymbol Interference (ISI)
Pulse spreading in an optical signal, after traversing along optical fiber,
leads to ISI. Some fraction of energy remaining in appropriate time slot
is designated by , so the rest is the fraction of energy that has spread
Into adjacent time slots.


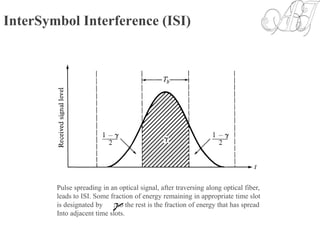
5. Receiver Configuration
The binary digital pulse train incident on the photodetector can be written in the
following form:
t.allforpositiveiswhichshapepulsereceivedtheis)(and
digitmessageththeofparameteramplitudeanisperiod,bitiswhere
)()(
th
nbT
nTthbtP
p
nb
n
bpn


 [7-3]

6. • In writing down eq. [7-3], we assume the digital pulses with amplitude V
represents bit 1 and 0 represents bit 0. Thus can take two values
corresponding to each binary data. By normalizing the input pulse to
the photodiode to have unit area
represents the energy in the nth pulse.
the mean output current from the photodiode at time t resulting from pulse
train given in eq. [7-3] is (neglecting the DC components arising from dark
current noise):
nb
)(thp



1)( dtthp
nb




n
bpno nTthbMtMP
h
q
ti )()()(


[7-4]

7. Bit Error Rate (BER)
• Probability of Error= probability that the output voltage is
less than the threshold when a 1 is sent + probability that the
output voltage is more than the threshold when a 0 has been
sent.
b
e
t
e
TB
Bt
N
N
N
t
t
/1
duringedtransmittpulsesof#total
intervalmecertain tiaovererrorof#
ErrorofyProbabilitBER



[7-5]

8. Probability distributions for received logical 0 and 1 signal pulses.
the different widths of the two distributions are caused by various signal
distortion effects.
thv
edtransmitt0if,exceedstageoutput volequalizerthat theprobablity)0|()(
edtransmitt1if,thanlessistageoutput volequalizerthat theprobablity)1|()(
0
1
vdyypvP
vdyypvP
v
v






[7-6]

9. • Where are the probabilities that the transmitter sends 0 and 1
respectively.
• For an unbiased transmitter





th
th
v
v
ththe
dyypqdyypq
vPqvPqP
)1|()1|(
)()(
01
0011
[7-7]
01 and qq
5.010  qq
10 1 qq 

10. Gaussian Distribution
dv
bv
dyypvP
dv
bv
dyypvP
thth
thth
vv
th
v
on
v
th









 






 

2
off
2
off
off
0
2
on
2
on
1
2
)(
exp
2
1
)0|()(
2
)(
exp
2
1
)1|()(


mea
n
mea
n
[7-8]

11. • If we assume that the probabilities of 0 and 1 pulses are equally likely, then
using eq [7-7] and [7-8] , BER becomes:
Q
Q
Q
dxxQP
Q
e
/2)exp(-
2
1
)
2
(erf1
2
1
)exp(
1
)(BER
2
2/
2









 

[7-9]
dyyx
vbbv
Q
x
thth
 




0
2
on
on
off
off
)exp(
2
)(erf


[7-9]
[7-10]

12. Approximation of error function
Variation of BER vs Q,
according to eq [7-9].

13. Special Case
In special case when:
Vbb  onoffonoff ,0&
From eq [7-29], we have: 2/Vvth 
Eq [7-8] becomes:






 )
22
(erf1
2
1
)(


V
Pe
[7-11]
Study example 7-1 pp. 286 of the textbook.
ratio.noise-rms-to-signalpeakis

V

14. Quantum Limit
• Minimum received power required for a specific BER assuming that the
photodetector has a 100% quantum efficiency and zero dark current. For
such ideal photo-receiver,
• Where is the average number of electron-hole pairs, when the incident
optical pulse energy is E and given by eq [7-1] with 100% quantum
efficiency .
• Eq [7-12] can be derived from eq [7-2] where n=0.
• Note that, in practice the sensitivity of receivers is around 20 dB higher than
quantum limit because of various nonlinear distortions and noise effects in
the transmission link.
)exp()0(1 NPPe  [7-12]
N
)1( 

15. Eye Diagram
• Standard measure for signaling
• Synchronized superposition of all possible realizations of the signal
viewed within a particular interval
• Obtained from measurement or transient simulation
TX RX
channel

16. Eye Diagram (cont’d)
• Timing jitter
• Deviation of the zero-crossing from its ideal occurrence time
• Amplitude noise
• Set by signal-to-noise ratio (SNR)
• The amount of noise at the sampling time

17. Existing Work
• Eye diagram analysis
• Analytical eye-diagram model [Hashimoto, CICC’07]
• Only consider attenuation and reflection
• Assume perfect match at transmitter end
• Jitter and noise analysis
• Data-dependent jitter model [Buckwalter, MicrowaveSymp’04][Ou’DTS’04]
• Only consider two taps of channel response
• Enumerate all possible input combinations: [00, 01, 10, 11]
• Clock jitter model [Hanumolu’04][Tao’99]
• Clock-data recovery (CDR), DLL, PLL
• Amplitude noise model [Hanumolu’05]
• No general framework to model the jitter and noise and find
out what is the worst possible scenario

18. Eye Mask
• Wider eye = more timing margin
• Higher eye = more noise margin
• How to determine if the eye satisfies the mask or not
• Find the worst-case jitter and noise
PCI-Express

19. Contribution
• Formula-based model for jitter and noise
• Use differential signaling as an example
• Utilize multi-conductor transmission line equations
• Can be extended to equalized link
• Consider the pre-emphasis filter at the transmitter end
• Worst-case jitter and noise
• Directly find the worst-case input pattern
• Use efficient mathematical programming algorithms
• No need for time-consuming simulation
• Runtime is not determined by the pattern length
• Adequate length can be used according to channel response

20. Motivations
• Higher Spectral Efficiency – QPSK / multi-level QAMs
• Higher Data Rates – 40Gbit/s, 100Gbit/s, and even higher
• Higher Receiving Sensitivity
Recent Coherent Optical Communication
• Coherent detection based on DSP
• Local oscillator (LO) laser
• Polarization diversity 90° optical hybrid
• Balanced detectors
• High speed analog to digital convertor (ADC)
• High speed digital signal processing (DSP)
Coherent Optical

21. Coherent Optical Communications
Coherent Optical Receiver – I
• Advantages:
• Multi-level constellations
• High data rate
• Phase managements
• Polarization managements
• Dis-advantages:
• Electrical circuit complexity
• Speed limitations
• Cost issues
• Power consumptions

22. Coherent Optical Receiver – II
• Homodyne OPLL based coherent receiver – Costas Loop
• Optical carrier recovering technique
Requiring Stable OPLL

23. Coherent Optical Receiver – II
• Challenges:
• Long loop delays (*1ns)
• Narrow loop bandwidth (*100MHz)
• Transmitting and LO lasers’ linewidth
• Sensitive by external variations
• Solutions:
• Integrated circuits (photonic IC, electrical IC)
• Feed-forward loop filter topology
• Minimizing Interconnection delays
• Digitally operating feedback system

24. Phase Locked Coherent BPSK Receiver
Homodyne OPLL + Costas Loop
• Three blocks: photonic IC, electrical IC, and hybrid loop filter
• High speed BPSK data demodulations

25. Phase Locked Coherent BPSK Receiver
Photonic IC
• SG-DBR laser – 40nm tunable ranges
• 90° optical hybrid
• 4 un-balance photodiodes – 30GHz bandwidth

26. Phase Locked Coherent BPSK Receiver

27. Phase Locked Coherent BPSK Receiver
Electrical IC
• Limiting amplifiers
• Phase / frequency detector (PFD) – XOR + delay line
Teledyne’s
500nm InP HBT
300GHz ft / fmax

28. Phase Locked Coherent BPSK Receiver

29. Phase Locked Coherent BPSK Receiver
Loop Filter
• Main path by integrator – high gain at DC and low frequencies
• Feed-forward path – passive capacitor component
Main Path
Feed-Forward Path
Open Loop Responses
* Challenges:
1. OP amp has lots of delays
2. OP amps bandwidth is limited (100MHz)

30. Fabricated in UCSB (Mingzhi Lu)
Designed by Eli Bloch using
Teledyne 500nm HBT ProcessLoop filter and system
designed by Hyun-chul Park
Integration on a Single Carrier board
• Compact chip size of 10 x 10mm2
• Total delay (120ps)=PIC (40ps)+EIC (50ps)+Interconnection
(30ps)
1GHz Loop Bandwidth is feasible

31. THANK YOU!