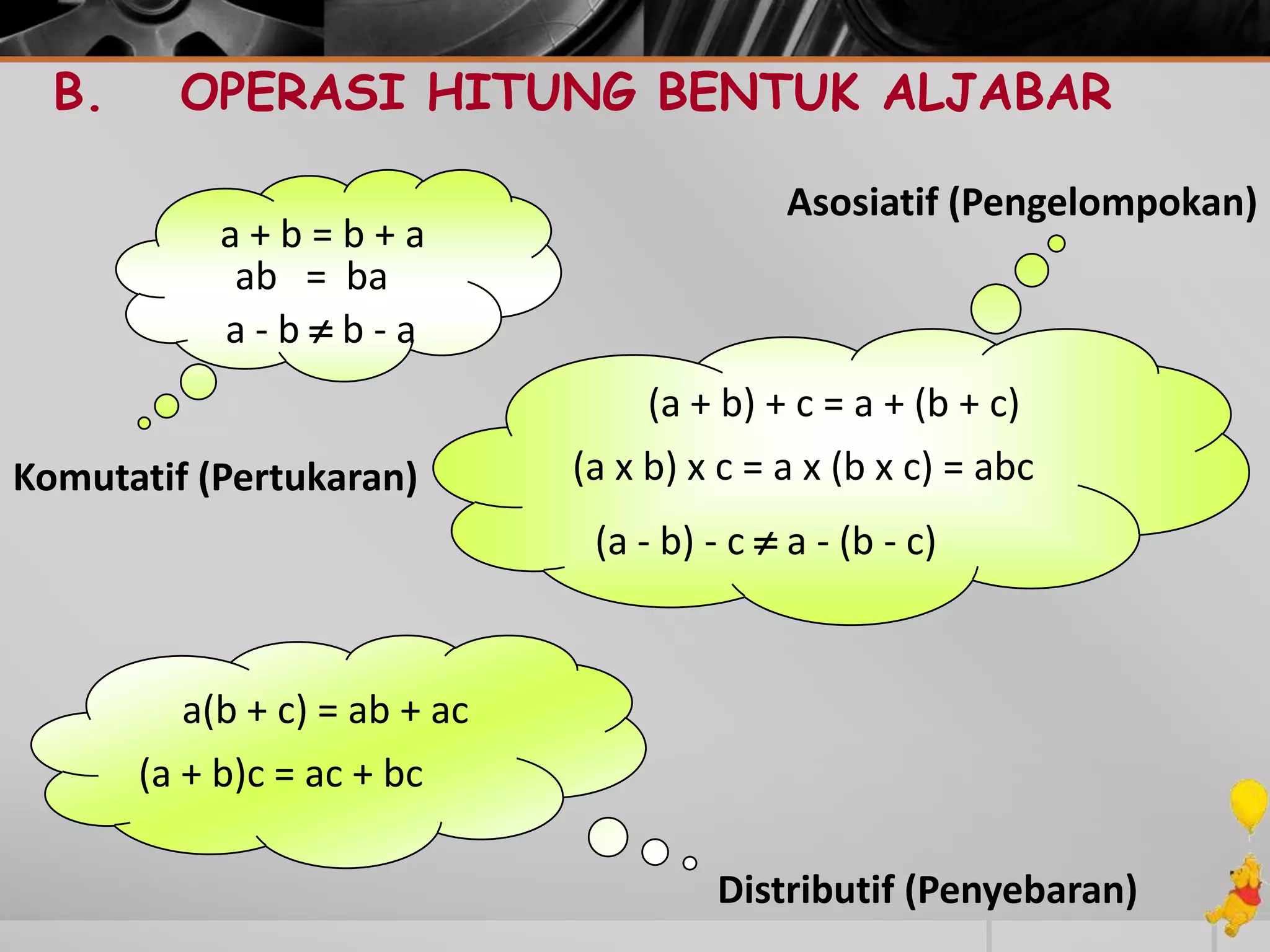
Dokumen ini membahas operasi pada bentuk aljabar, termasuk identifikasi konstanta, koefisien, suku, dan metode perkalian dan pembagian bentuk aljabar. Contoh-contoh disertakan untuk memperjelas konsep perkalian antara konstanta dengan bentuk aljabar serta penerapan sifat distributif. Terdapat juga penjelasan tentang operasi perpangkatan dan penyederhanaan bentuk aljabar.

1. OPERASI
pada bentuk
ALJABAR

5. 2. Konstanta
Suku dari suatu bentuk aljabar yang berupa bilangan dan tidak memuat
variabel
Contoh: Tentukan konstanta pada bentuk aljabar 2x2 + 3xy + 7x – y – 8
Penyelesaian:
konstanta adalah suku yang tidak memuat variabel, sehingga yang konstanta
dari 2x2 + 3xy + 7x – y – 8
adalah -8
3.Koefisien
Konstanta dari suatu suku pada bentuk aljabar
Contoh: Tentukan koefisien x pada bentuk aljabar berikut: 5x2y + 3x
Penyelesaian :
koefisien x dari 5x2y + 3x adalah 3

6. 4. Suku
Adalah variabel beserta koefisiennya atau konstanta pada bentuk
aljabar yang dipisahkan oleh operasi jumlah atau selisih.
suku sendiri dibagi tiga yaitu:
a. suku satu adalah bentuk aljabar yang tidak dihubungkan oleh
operasi jumlah atau selisih.
contoh: 3x, 4a2, – 2ab,….
b. suku kedua adalah bentuk aljabar yang dihubungkan oleh satu
operasi jumlah atau selisih.
contoh: a2 + 2,x + 2y, 3x2 – 5x,…
c. suku ketiga adalah bentuk aljabar yang dihubungkan oleh dua
operasi jumlah atau selisih.
Contoh: 3x2 + 4x – 5, 2x + 2y – xy,…

7. B. OPERASI HITUNG BENTUK ALJABAR
a + b = b + a
ab = ba
a - b  b - a
Komutatif (Pertukaran)
Asosiatif (Pengelompokan)
(a + b) + c = a + (b + c)
(a x b) x c = a x (b x c) = abc
(a - b) - c  a - (b - c)
Distributif (Penyebaran)
a(b + c) = ab + ac
(a + b)c = ac + bc

8. PENJUMLAHAN DAN PENGURANGAN
BENTUK ALJABAR
Penjumlahan dan pengurangan
suku-suku sejenis dapat dilakukan
jika suku-suku tersebut memiliki:
a. Variabelnya sama
b. Pangkat variabelnya sama
a. Variabelnya sama
b. Pangkat variabelnya sama
B. Operasi Hitung Pada Bentuk
Aljabar

9. Contoh
5x2 + 7xy + 3x2 + 5x2y – 5xy + 7y
5x2 3x2 5x2 + 3x2
7xy -5xy 7xy– 5xy
8x2
2xy

10. PERKALIAN BENTUK ALJABAR
a. Perkalian antara konstanta dengan
bentuk aljabar
b. Perkalian antara dua bentuk aljabar
B. Operasi Hitung Pada Bentuk
Aljabar

11. a. Perkalian antara konstanta dengan
bentuk aljabar
Perkalian suatu bilangan konstanta k
dengan bentuk aljabar suku satu dan suku dua
dinyatakan sebagai berikut:
k(ax) = kax
k(ax + b) = kax + kb
x(x + 4) = x2 4x+

12. a. 4(p + q)
b. 5(ax + by)
c. 3(x – 2) + 6(7x + 1)
d. –8(2x – y + 3z)
Penyelesaian:
a. 4(p + q) = 4p + 4q
b. 5(ax + by) = 5ax + 5by
c. 3(x – 2) + 6(7x + 1) = 3x – 6 + 42x + 6
= (3 + 42)x – 6 + 6
= 45x
d. –8(2x – y + 3z) = –16x + 8y – 24z
Contoh:

13. b. Perkalian antara dua bentuk aljabar
memanfaatkan sifat distributif perkalian terhadap
penjumlahan dan sifat distributif perkalian
terhadap pengurangan.

14. (x+2) (x+3) = x2 3x+ +
2x + 6
(x+2)(x+3)= x2 + 5x + 6(x+2)(x+3)= x2 + 5x + 6

15. Contoh Soal :
Tentukan hasil perkalian suku dua berikut,
kemudian sederhanakan
a. (2x + 4)(3x + 1)
b. (–3x + 2)(x – 5)

17. Pembagian bentuk aljabar akan lebih
mudah jika dinyatakan dalam bentuk
pecahan.
B. Operasi Hitung Pada Bentuk
Aljabar

18. Contoh Soal :
Tentukan hasil pembagian berikut.
a. 8x : 4 c. 16a2b : 2ab
b. 15pq : 3p d. (8x2 + 2x) : (2y2 – 2y)
Jawab:

19. PERPANGKATAN BENTUK ALJABAR
Untuk a bilangan riil dan n bilangan asli
B. Operasi Hitung Pada Bentuk
Aljabar
operasi perpangkatan diartikan sebagai
operasi perkalian berulang dengan unsur
yang sama, untuk sebarang bilangan bulat
a, berlaku:

21. PENGKUADRATAN SUKU
DUA
(a + b)2 (a + b) (a + b)=
a2
+ 2ab + b2=
(a - b)2 (a - b) (a - b)=
a2
- 2ab + b2=

22. (a + b)3 = (a + b) (a + b)2
= (a + b) (a2 + 2ab + b2)
(a+b)2 = a2 + 2ab + b2
= a(a2 + 2ab + b2 ) + b (a2 + 2ab + b2 )
(menggunakan cara skema)
= a3 + 2a2b + ab2 + a2b + 2ab2 + b3
(suku yang sejenis dikelompokkan)
= a3 + 2a2b + a2b + ab2 +2ab2 + b3
(operasikan suku yg sejenis)
= a3 + 3a2b + 3ab2 + b3

23. Sekian
Dan
Terima Kasih

25. 1. Sederhanakan bentuk berikut ini.
a. 6p + 5pq – 2q – 4p + 3pq – 7q
b. 4(x + 3y) + 3(x – 4y)
2. Tentukan hasil perkalian Suku Dua dibawah ini.
c. (x + 3)(x – 2)
d. (4x – 2)(x – 3)
4. Tentukan hasil pengkuadratan berikut ini.
g. (2x + 3)2
h. (3p – 5)2
3. Sederhanakanlah pembagian bentuk aljabar
berikut
e. 3xy : 2y
f. 6a3b2 : 3a2 b

26. Pembahasan:
2p= 8pq+
a. 6p + 5pq – 2q – 4p + 3pq – 7q
- 9q2p + 8pq – 9q
b. 4(x + 3y) + 3(x – 4y)
7x= 7x
4x + 12y + -3x 12y=
0+

27. c. (x + 3)(x - 2)
(x + 3) (x - 2) = x2 2x- +
3x - 6
(x+3)(x-2)= x2 + x - 6(x+3)(x-2)= x2 + x - 6

28. d. (4x - 2)(x - 3)
(4x - 2) (x - 3) = 4x2 12x- -
2x + 6
(4x - 2)(x - 3)= 4x2 - 10x - 6(4x - 2)(x - 3)= 4x2 - 10x - 6

29. e. 3xy : 2y
f. 6a3b2 : 3a2 b
=

30. (2x+3)2 (2x +3) (2x + 3)=
4x2 + 6x + 9=
g. (2x + 3)2
4x2 + 12x + 9=
6x +
4x2 + 12x + 9

31. (3p - 5)2 (3p - 5) (3p - 5)=
9p2
- 15p - 25=
h. (3p - 5)2
9p2 - 30p + 25=
15p +
9p2 – 30p + 25