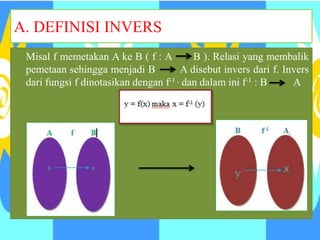
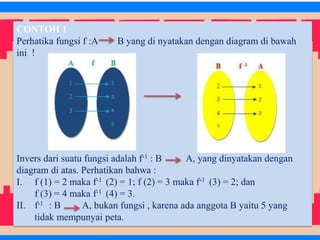
Dokumen ini membahas konsep fungsi invers, termasuk syarat dan sifat fungsi untuk memiliki invers, serta cara menentukan fungsi invers dari berbagai jenis fungsi seperti linear, rasional, dan kuadrat. Selain itu, dokumen ini memberikan contoh dan latihan untuk memperkuat pemahaman siswa tentang topik ini. Pembaca juga diajarkan bagaimana memecahkan masalah nyata menggunakan fungsi invers.

1. FUNGSI INVERS
Oleh : Ayun Sri Rahmani

2. Kompetensi Dasar
1. Memahami konsep fungsi dan menerapkan operasial
aljabar pada fungsi.
2. Menganalisis konsep dan sifat suatu fungsi dan
melakukan manipulasi aljabar dalam menentukan invers
fungsi dan fungsi invers.
3. Memahami dan menganalisis sifat suatu fungsi sebagai
hasil operasi dua atau lebih fungsi yang lain.
4. Memilih strategi yang efektif dan menyajikan model
matematika dalam memecahkan masalah nyata terkait
fungsi invers dan invers fungsi

3. Indikator
1. Siswa dapat menjelaskan syarat agar suatu fungsi
mempunyai invers.
2. Siswa dapat mengetahui sifat-sifat invers
3. Siswa dapat menentukan fungsi invers dari suatu
fungsi linear, rasional kuadrat dan komposisi.
4. Siswa dapat menentukan nilai fungsi invers dari
suatu fungsi linear, rasional kuadrat dan komposisi.
5. Siswa dapat mengidentifikasi sifat-sifat fungsi
invers

4. A. DEFINISI INVERS
Misal f memetakan A ke B ( f : A B ). Relasi yang membalik
pemetaan sehingga menjadi B A disebut invers dari f. Invers
dari fungsi f dinotasikan dengan f-1 , dan dalam ini f-1 : B A

5. CONTOH 1
Perhatika fungsi f :A B yang di nyatakan dengan diagram di bawah
ini !
Invers dari suatu fungsi adalah f-1 : B A, yang dinyatakan dengan
diagram di atas. Perhatikan bahwa :
I. f (1) = 2 maka f-1 (2) = 1; f (2) = 3 maka f-1 (3) = 2; dan
f (3) = 4 maka f-1 (4) = 3.
II. f-1 : B A, bukan fungsi , karena ada anggota B yaitu 5 yang
tidak mempunyai peta.

6. CONTOH II
Perhatikan fungsi g : A B yang dinyatkan dengan diagram
di bawah ini!
Invers dari suatu fungsi adalah g-1 : B A, yang dinyatakan
dengan diagram di atas. Perhatikan bahwa :
I. g(1) = a maka g-1 (a) = 1; g (2) = b maka g-1 (b) = 2; dan g(3)
= c maka g-1 (c) = 3.
II. g-1 : B A, adalah fungsi, karena tidak ada anggota yang
tidak mempunyai peta.

7. B. Fungsi Invers dari Fungsi Linear
Untuk fungsi f(X) = ax + b dapat dicari fungsi inversnya
sebagai berikut!

8. Contoh
Jika fungsi f(x) = 2x + 1, maka f-1 (x) adalah….?
Jawab :
f(x) = 2x + 1
f(x) = 2x + 1 = y
= 2x = y – 1
= x = y – 1 / 2
f-1(y) = y – 1 / 2
f-1(x) = x – 1 / 2
Jadi, f-1(x)adalah y – 1 / 2

9. C. Fungsi Invers dari Fungsi Rasional

10. D. Fungsi Invers dari Fungsi Kuadrat

11. Catatan
Invers fungsi akan akan merupakan fungsi jika di penuhi syarat-
syarat sebagai fungsi.

13. Contoh :
Rumus invers dari fungsi f(x) = x2 – 6x + 9
Jawab :

14. E. Fungsi invers dari fungsi bentuk akar

15. Contoh :

16. F. Fungsi komposisi invers
Fungsi Komposisi Komposisi Fungsi Invers

17. Contoh :
f(x) = 2x + 1; f(g) = 3x -1, tentukan (fog) -1(x) = …?
Jawab :
(fog) (x) = f(g(x))
= f (3x -1)
= 2 (3x -1) + 1
= 6x -1 = y
= 6x = y + 1
= x = (y + 1)/6
(fog) -1(y) = (y + 1)/6
(fog) -1(x) = (x + 1)/6
Jadi , (fog) -1(x) = (x + 1)/6

18. Soal-soal latihan
No 1 (a,b,c) No 3 No 4 No 5 No 6 (a,b)No 2
JAWABAN

19. a. f(x) = 4x -1
= 4x – 1 = y
= 4x = y + 1
= x = ( y + 1) / 4
f-1 (y) = ( y + 1) / 4
f-1 (x) = ( x + 1) / 4
Jadi, f-1 (x)= ( x + 1) / 4
b. f(x) = x -7
= x – 7 = y
= x = y + 7
f-1 (y) = y + 7
f-1 (x) = x + 7
Jadi, f-1 (x)= x + 7
Jawaban No 1
c. f(x) = 3x + 8
= 3x + 8 = y
= 3x = y – 8
= x = (y- 8) / 3
f-1 (y) = (y- 8) / 3
f-1 (x) = (x- 8) / 3
Jadi, f-1 (x) = (x- 8) / 3
BACK

20. Jawaban No 2
BACK

21. Jawaban No 3
BACK

22. Jawaban No 4
BACK

23. Jawaban No 5
(fog)(x) = f(g(x))
= f ( x + 8)
=( x + 8 ) + 4
= x + 12 = y
= x = y – 12
(fog)-1(y) = y – 12
(fog)-1(x) = x – 12
BACK

24. Jawaban No 6
a. (f ₀g)(x) = f (g(x))
= f ( x + 5 )
= (x + 5) – 1
= x + 4= y
= x = y - 4
(f ₀g)-1(y) = y – 4
(f ₀g)-1(x) = x – 4
(f ₀g)-1(1) = 1 – 4 = 3
Jadi, (f ₀g)-1(1)= 1 – 4 = 3
b. (g ₀ f)(- 2) = g(f(x)) = -2
= g ( x – 1) = -2
= (x – 1) + 5 = -2
= x + 4 = - 2
= x = 6
Jadi, (g ₀ f)-1(-2) = 6
BACK

25. THANKS 