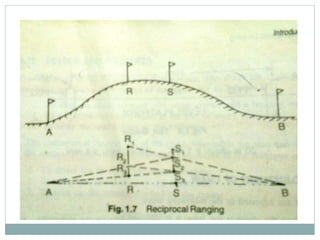
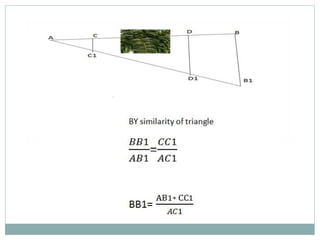
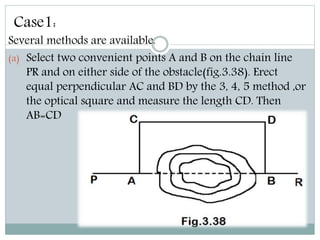
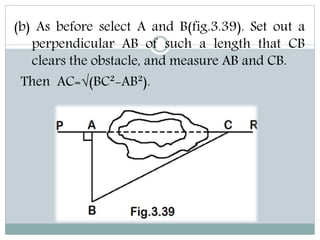
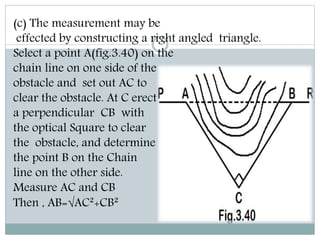
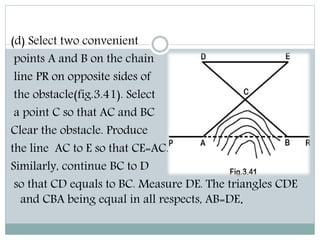
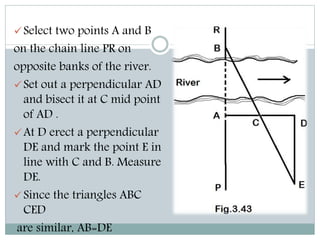
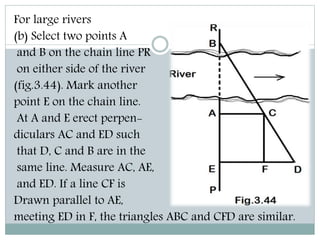
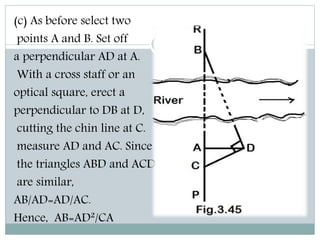
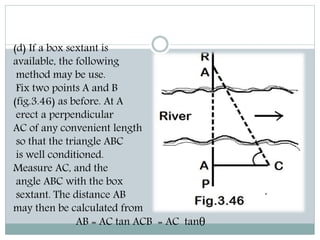
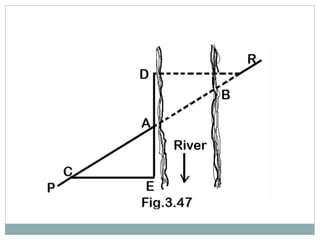
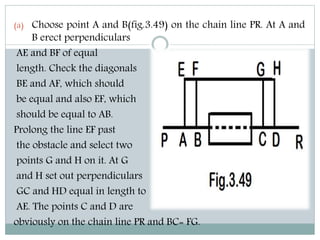
The document discusses various methods for measuring distances across obstacles during land surveying. It classifies obstacles as: 1) Chaining free but vision obstructed, 2) Chaining obstructed but vision free, and 3) Both chaining and vision obstructed. For each type, it provides examples and explains specific measurement techniques such as reciprocal ranging, using random lines, constructing right triangles, and prolonging the line beyond obstacles to determine distances.

1. Obstacles in Chaining
By: Engr.M.Z.J
QUCEST, LARKANA,

2. Various obstacles or obstructions such as
woods, hills, rivers, buildings, etc., are
continually met with an chaining. It is
however, essential that chaining should be
continued in a straight line. Special
methods are, therefore, employed in
measuring distances across the
obstructions.

3. The various obstacles may be
classified as:
1) CHAINING FREE BUT VISION
OBSTRUCTED
2) CHAINING OBSTRUCTED BUT
VISION FREE
3) BOTH CHAINING AND VISION ARE
OBSTRUCTED.

4. (1) Chaining free, Vision obstructed:
e.g. rising ground or a hill intervening,
jungle etc. In this type of obstacle, the ends of a
line are not intervisible. There are two cases to
be considered:
1. Both ends may be visible from intermediate
points on the line.
2. Both ends may not be visible from any
intermediate point.

5. Case1:
In this case the difficulty may be got over by
reciprocal ranging.
Reciprocal ranging:
When the end stations are not intervisible due to
there being high ground between them,
intermediate ranging rods are fixed on the line
in an indirect way. These method is now, as
indirect ranging or reciprocal ranging.

7. Case2:
This case occurs when it is desired to run a line across a
wooded field, the trees, underbrush preventing the fixing
of intermediate stations. In such a case, the method of
the random line is the most suitable.
Let AB be the line whose length is required. From A run
a line(AB1), called a random line, in any convenient
direction, but as nearly towards B as can be judged and
continue it until the point B is visible from B1. chain the
line to B1 where BB1 is perpendicular to AB1 and
measure BB1. Then,
AB=√(AB1)² +(BB1) ²

9. If any other length AC1 is measured along
AB1 a point C is located on the line AB by
measuring the perpendicular distance
C1C=(AC1/AB1)×B1B.
In this manner a sufficient number of
points can be located. The line is then cleared
and the distance measured.

10. (2) Chaining Obstructed, but Vision Free:
e.g. a pond plantation, tank, river, etc. The
problem is to find the distance between two
convenient points on the chain line on either
side of the obstacle. There are two cases :
1. In which it is possible to chain round obstacle
e.g. a pond, a bend in the river, etc.
2. In which it is not possible to chain round the
obstacle, e.g. a river.

11. Case1:
Several methods are available.
(a) Select two convenient points A and B on the chain line
PR and on either side of the obstacle(fig.3.38). Erect
equal perpendicular AC and BD by the 3, 4, 5 method ,or
the optical square and measure the length CD. Then
AB=CD

12. (b) As before select A and B(fig.3.39). Set out a
perpendicular AB of such a length that CB
clears the obstacle, and measure AB and CB.
Then AC=√(BC²-AB²).

13. (c) The measurement may be
effected by constructing a right angled triangle.
Select a point A(fig.3.40) on the
chain line on one side of the
obstacle and set out AC to
clear the obstacle. At C erect
a perpendicular CB with
the optical Square to clear
the obstacle, and determine
the point B on the Chain
line on the other side.
Measure AC and CB
Then , AB=√AC²+CB²

14. (d) Select two convenient
points A and B on the chain
line PR on opposite sides of
the obstacle(fig.3.41). Select
a point C so that AC and BC
Clear the obstacle. Produce
the line AC to E so that CE=AC.
Similarly, continue BC to D
so that CD equals to BC. Measure DE. The triangles CDE
and CBA being equal in all respects, AB=DE.

15. CASE 2:
The typical example of this class of obstacle is a
river. There are several methods ,of which a few
given below ;

16. Select two points A and B
on the chain line PR on
opposite banks of the river.
Set out a perpendicular AD
and bisect it at C mid point
of AD .
At D erect a perpendicular
DE and mark the point E in
line with C and B. Measure
DE.
Since the triangles ABC
CED
are similar, AB=DE

17. For large rivers
(b) Select two points A
and B on the chain line PR
on either side of the river
(fig.3.44). Mark another
point E on the chain line.
At A and E erect perpen-
diculars AC and ED such
that D, C and B are in the
same line. Measure AC, AE,
and ED. If a line CF is
Drawn parallel to AE,
meeting ED in F, the triangles ABC and CFD are similar.

18. Therefore,
AB/AC=CF/FD
: but
CF=AE and FE=ED-AC
or AB/AC=AE/(ED-AC)
whence,
BA=(AC×AE)/(ED-AC)

19. (c) As before select two
points A and B. Set off
a perpendicular AD at A.
With a cross staff or an
optical square, erect a
perpendicular to DB at D,
cutting the chin line at C.
measure AD and AC. Since
the triangles ABD and ACD
are similar,
AB/AD=AD/AC.
Hence, AB=AD²/CA

20. (d) If a box sextant is
available, the following
method may be use.
Fix two points A and B
(fig.3.46) as before. At A
erect a perpendicular
AC of any convenient length
so that the triangle ABC
is well conditioned.
Measure AC, and the
angle ABC with the box
sextant. The distance AB
may then be calculated from
AB = AC tan ACB = AC tanθ

21. (e) This method is used when a survey line crosses
a river obliquely. Set out line AE(fig.3.47) at a
convenient angle with the survey line PR and
range point D in line with E and A, making
AD=AE. Using an optical square, set out
perpendiculars DB and EC to the line DE at D
and E, intersecting the survey line PR at B and C
respectively. Measure AC. The triangles ADB
and AEC being congruent, the required length
AB is equal to AC.

23. (3) Chaining and Vision both obstructed:
In this case the problem consists in
prolonging the line beyond the obstacle
and determining the distance across it. A
building is a typical example of this class
of obstacle.

24. (a) Choose point A and B(fig.3.49) on the chain line PR. At A and
B erect perpendiculars
AE and BF of equal
length. Check the diagonals
BE and AF, which should
be equal and also EF, which
should be equal to AB.
Prolong the line EF past
the obstacle and select two
points G and H on it. At G
and H set out perpendiculars
GC and HD equal in length to
AE. The points C and D are
obviously on the chain line PR and BC= FG.

25. Great care must be taken in setting out
the perpendiculars very accurately
and to see that their lengths are
exactly equal.

26. Thank You..