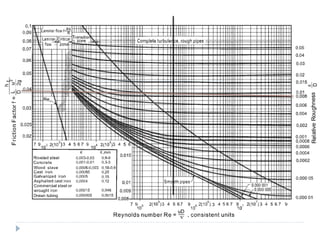
1) The document discusses methods for calculating the friction factor f in turbulent pipe flow. 2) It provides equations from Swamee-Jain, Haaland, and Churchill that can be used to explicitly calculate f based on parameters like Reynolds number, relative roughness, and pipe diameter. 3) The example problem calculates f for water flowing in a ductile iron pipe, finding f=0.038 using Moody's diagram and the relative roughness of the pipe material.

1. Friction Factor Numerical
QUEST CAMPUS LARKANA
17CE

2. Friction Loss in Turbulent Flow
2
 For commercially available pipe and tubing, the design value of the
average wall roughness has been determined as shown in the
following table

3. Problem
3
 Statement: Determine the friction factor f if water at 70oC is flowing
at 9.14 m/s in an uncoated ductile iron pipe having an inside
diameter of 25 mm.
 Solution: The Reynolds number must first be evaluated to
determine whether the flow is laminar or turbulent:
  
 
5
27
27
1065
10114
0250149
10114
0250149
x.
smx.
m.sm.
Re
smx.
,m.D,sm.V
VD
Re









5. Problem
5
 Thus, the flow is turbulent. Now the relative roughness must be
evaluated. From previous table we find ε=2.4x10-4 m. Then , the
relative roughness is
 The final steps in the procedure are as follows:
1. Locate the Reynolds number on the abscissa of the Moody
Diagram.
2. Project vertically until the curve for ε/D =0.00961538 is reached.
3. Project horizontally to the left, and read f=0.038
009615380
0250
41042
.
m.
mx.
D





6. Roughness Height (e or ε) for Certain
Common Pipes
6
ε

7. Empirical Solutions for Friction Factor f
7
 Colebrook Equation The Colebrook Equation can be
used to determine friction factor,f. It describes the
curves of Moody Diagram within the range of complete
 turbulent flow zone.
Unfortunately, it is an implicit form equation.
Therefore it must be solved using an iterative trial and
error procedure.

8. Empirical Solutions for Friction Factor f
8
 Benedict suggests the expression proposed by Swamee
and Jain, i.e.,
 While for ε/D>10-4 Haaland recommends
2
90
745
73
250



















.
DRe
.
D.
log
.
f
2
111
73
96
30860





















 


.
D D.Re
.
log
.
f

9. Empirical Solutions for Friction Factor f
9
 For situations where ε/D is very small, as in natural-gas
pipelines, Haaland proposes
Where n ~ 3
 The use of the Swamee-Jain or Haaland provide an
explicit formula of the friction factor in turbulent flow, and
is thus the preferred technique.
2
111
2
73
77
30860





















 







n.n
D D.Re
.
log
n.
f

10. Empirical Solutions for Friction Factor f
10
 For laminar flow (Re<2000) the usual Darcy-Weisbach
friction factor representation is
 For turbulent flow in smooth pipes (ε/D=0)
 For turbulent flow (Re>4000) the friction factor can be founded
from the Moody diagram
DRe
.
f
064

41
3160
/
DRe
.
f 

11. Empirical Solutions for Friction Factor f
11
 Churchill devised a single expression that represents the friction
factor for laminar, transition and turbulent flow regimes. This
expression, which is explicit for the friction factor given the
Reynolds number and relative roughness, is
 where
 and
 
121
51
12
18
8
/
.
D BARe
f
















   
16
90
2707
1
4572
















D.Re
ln.A .
D
16
53037







DRe
,
B