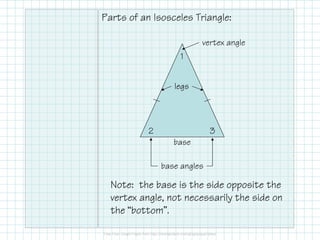
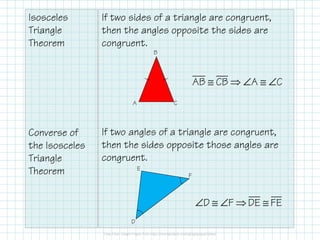
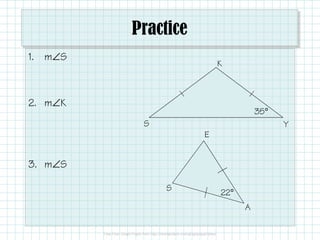
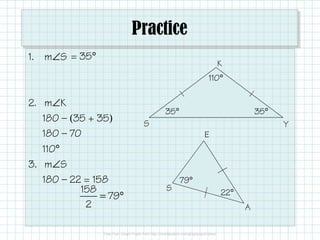
The document outlines the properties and theorems associated with isosceles and equilateral triangles, including their identification by side length and angle measures. It covers the isosceles triangle theorem and its converse, as well as the equilateral triangle corollary and its converse. Additionally, it includes practice problems to apply the concepts discussed.

1. Obj. 18 Isosceles and Equilateral
The student is able to (I can):
• Identify isosceles and equilateral triangles by side length
and angle measure
• Use the Isosceles Triangle Theorem to solve problems
• Use the Equilateral Triangle Corollary to solve problems

2. Parts of an Isosceles Triangle:
1
legs
vertex angle
2 3
base
base angles
Note: the base is the side opposite the
vertex angle, not necessarily the side on
the “bottom”.

3. Isosceles
Triangle
Theorem
Converse of
the Isosceles
Triangle
Theorem
If two sides of a triangle are congruent,
then the angles opposite the sides are
congruent.
C
B
A
AB @ CBÐA @ ÐC
If two angles of a triangle are congruent,
then the sides opposite those angles are
congruent.
F
E
D
ÐD @ ÐFDE @ FE

4. Equilateral
Triangle
Corollary
Converse of
the Equilateral
Triangle
Corollary
If a triangle is equilateral, then it is
equiangular.
C
B
A
@ @
AB BC CA
Ð @ Ð @ Ð
A B C
If a triangle is equiangular, then it is
equilateral.
Ð @ Ð @ Ð
D E F
DE EF FD
@ @
F
E
D

5. Practice
1. mÐS
2. mÐK
3. mÐS
35°
S
K
Y
S
E
A
22°

6. Practice
1. mÐS
2. mÐK
180 — (35 + 35)
180 — 70
110°
3. mÐS
180 — 22 = 158
35°
S
K
Y
S
E
A
22°
= 35°
35°
110°
= °
158
79
2
79°