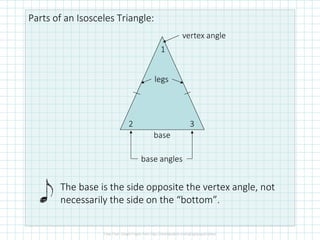
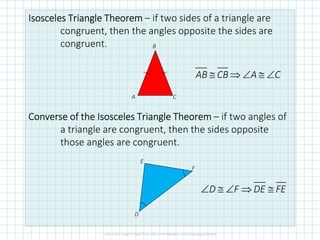
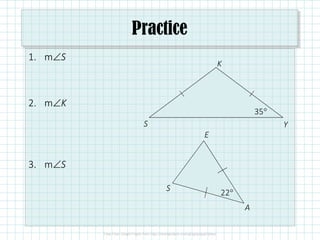
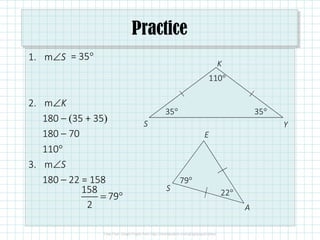
This document discusses isosceles and equilateral triangles. It defines isosceles triangles as triangles with two congruent sides and equilateral triangles as triangles with three congruent sides. The Isosceles Triangle Theorem and its converse state that if two sides or angles of a triangle are congruent, then the opposite angles or sides are also congruent. Similarly, the Equilateral Triangle Corollary and its converse state that if a triangle is equilateral, it is also equiangular, and vice versa. Examples are given to demonstrate using these properties to solve for missing angle measures.

1. Isosceles and Equilateral Triangles
The student is able to (I can):
• Identify isosceles and equilateral triangles by side length
and angle measure
• Use the Isosceles Triangle Theorem to solve problems
• Use the Equilateral Triangle Corollary to solve problems

2. Parts of an Isosceles Triangle:
The base is the side opposite the vertex angle, not
necessarily the side on the “bottom”.
1
2 3
legs
base
base angles
vertex angle

3. Isosceles TriangleIsosceles TriangleIsosceles TriangleIsosceles Triangle TheoremTheoremTheoremTheorem – if two sides of a triangle are
congruent, then the angles opposite the sides are
congruent.
ConverseConverseConverseConverse of the Isosceles Triangleof the Isosceles Triangleof the Isosceles Triangleof the Isosceles Triangle TheoremTheoremTheoremTheorem – if two angles of
a triangle are congruent, then the sides opposite
those angles are congruent.
C
B
A
AB CB A C≅ ⇒ ∠ ≅ ∠
F
E
D
D F DE FE∠ ≅ ∠ ⇒ ≅

4. Equilateral TriangleEquilateral TriangleEquilateral TriangleEquilateral Triangle CorollaryCorollaryCorollaryCorollary – if a triangle is equilateral, then
it is equiangular.
Converse of the Equilateral TriangleConverse of the Equilateral TriangleConverse of the Equilateral TriangleConverse of the Equilateral Triangle CorollaryCorollaryCorollaryCorollary – if a triangle is
equiangular, then it is equilateral.
C
B
A
≅ ≅
⇒ ∠ ≅ ∠ ≅ ∠
AB BC CA
A B C
D E F
DE EF FD
∠ ≅ ∠ ≅ ∠
⇒ ≅ ≅
F
E
D

5. Practice
1. m∠S
2. m∠K
3. m∠S
35°
S
K
Y
S
E
A
22°

6. Practice
1. m∠S
2. m∠K
180 – (35 + 35)
180 – 70
110°
3. m∠S
180 – 22 = 158
35°
S
K
Y
S
E
A
22°
= 35°
35°
110°
158
79
2
= °
79°