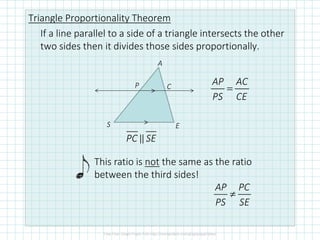
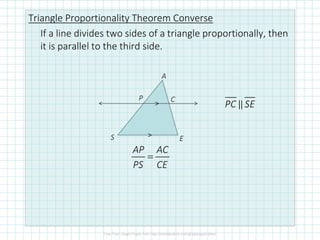
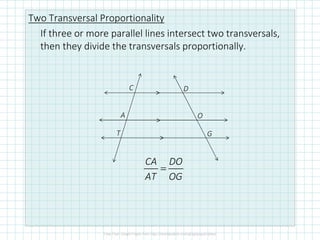
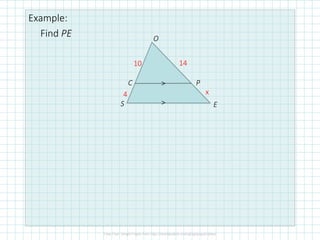
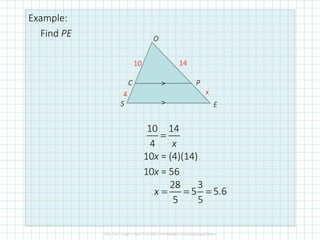
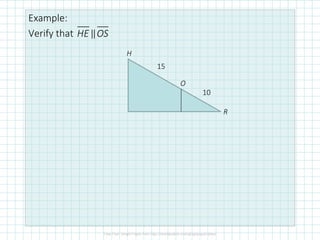
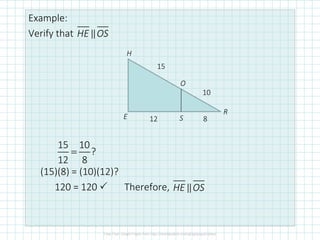
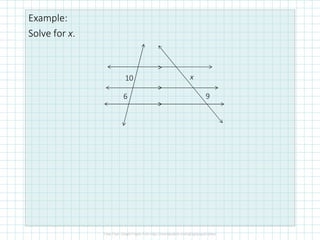
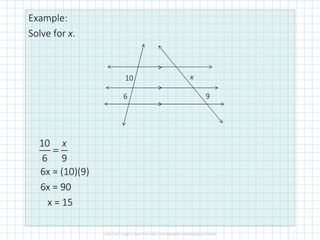
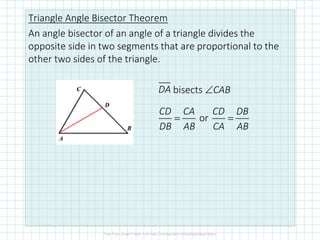
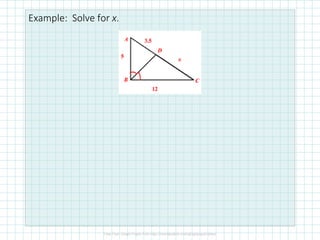
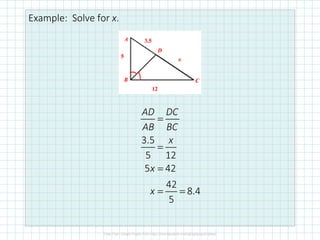
This document discusses proportionality theorems in triangles. It defines the triangle proportionality theorem and its converse, which state that if a line parallel to one side of a triangle intersects the other two sides, it divides them proportionally. It also discusses the two transversal proportionality theorem and the triangle angle bisector theorem. Examples are provided to illustrate using these theorems to find unknown side lengths and verify proportions.

1. Proportionality Theorems
The student is able to (I can):
• Use properties of similar triangles to find segment lengths.
• Apply proportionality and triangle angle bisector
theorems.
• Apply triangle angle bisector theorems

2. Triangle Proportionality Theorem
If a line parallel to a side of a triangle intersects the other
two sides then it divides those sides proportionally.
S
P
A
C
E
>
>
PC SE
AP AC
PS CE
=
This ratio is not the same as the ratio
between the third sides!
AP PC
PS SE
≠

3. Triangle Proportionality Theorem Converse
If a line divides two sides of a triangle proportionally, then
it is parallel to the third side.
S
P
A
C
E
>
>
PC SE
AP AC
PS CE
=

4. Two Transversal Proportionality
If three or more parallel lines intersect two transversals,
then they divide the transversals proportionally.
G
O
D
T
A
C
>
>
>
CA DO
AT OG
=

5. Example:
Find PE
S
C
O
P
E
10 14
4 x
>
>

6. Example:
Find PE
10x = (4)(14)
10x = 56
S
C
O
P
E
10 14
4
10 14
4 x
=
x
28 3
5 5.6
5 5
x = = =
>
>

7. Example:
Verify that
H
O
R
HE OS
15
10

8. Example:
Verify that
(15)(8) = (10)(12)?
120 = 120 Therefore,
H
O
R
SE
HE OS
15
10
12 8
15 10
?
12 8
=
HE OS

9. Example:
Solve for x.
>
>
>
x
96
10

10. Example:
Solve for x.
6x = (10)(9)
6x = 90
x = 15
>
>
>
x
96
10
10
6 9
x
=

11. Triangle Angle Bisector Theorem
An angle bisector of an angle of a triangle divides the
opposite side in two segments that are proportional to the
other two sides of the triangle.
bisects ∠CAB
or
CD CA CD DB
DB AB CA AB
= =
DA

12. Example: Solve for x.

13. Example: Solve for x.
3.5
5 12
5 42
42
8.4
5
AD DC
AB BC
x
x
x
=
=
=
= =