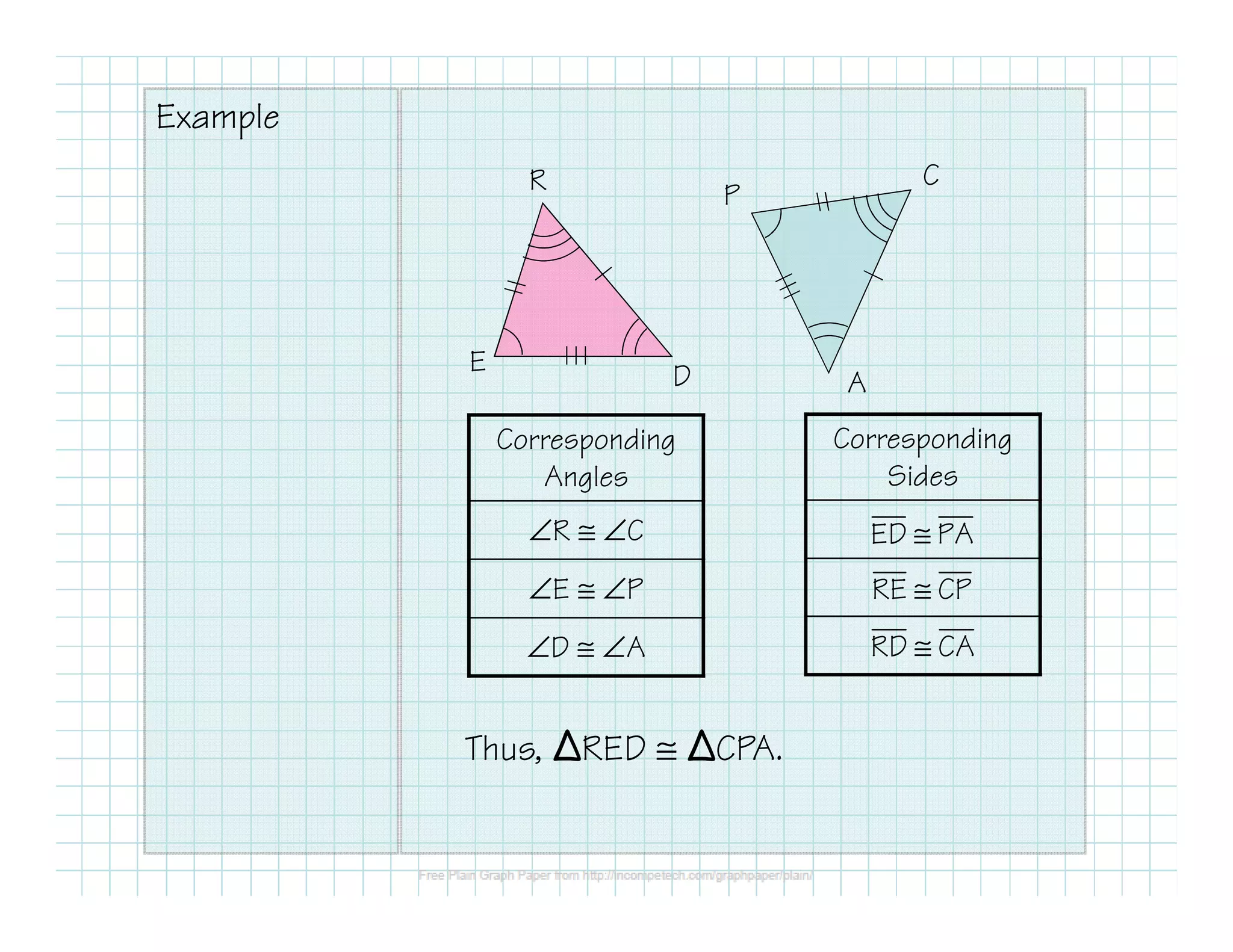
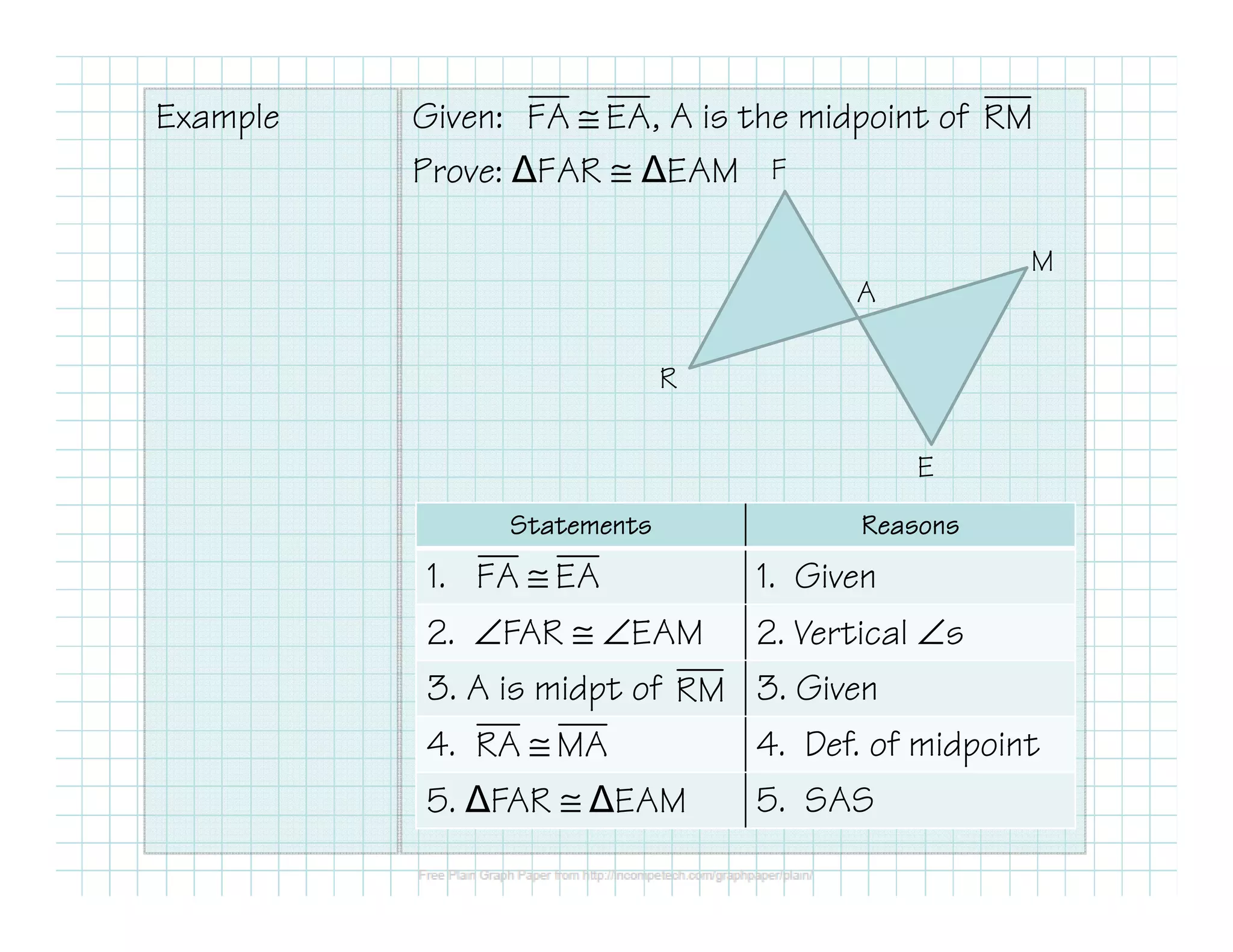
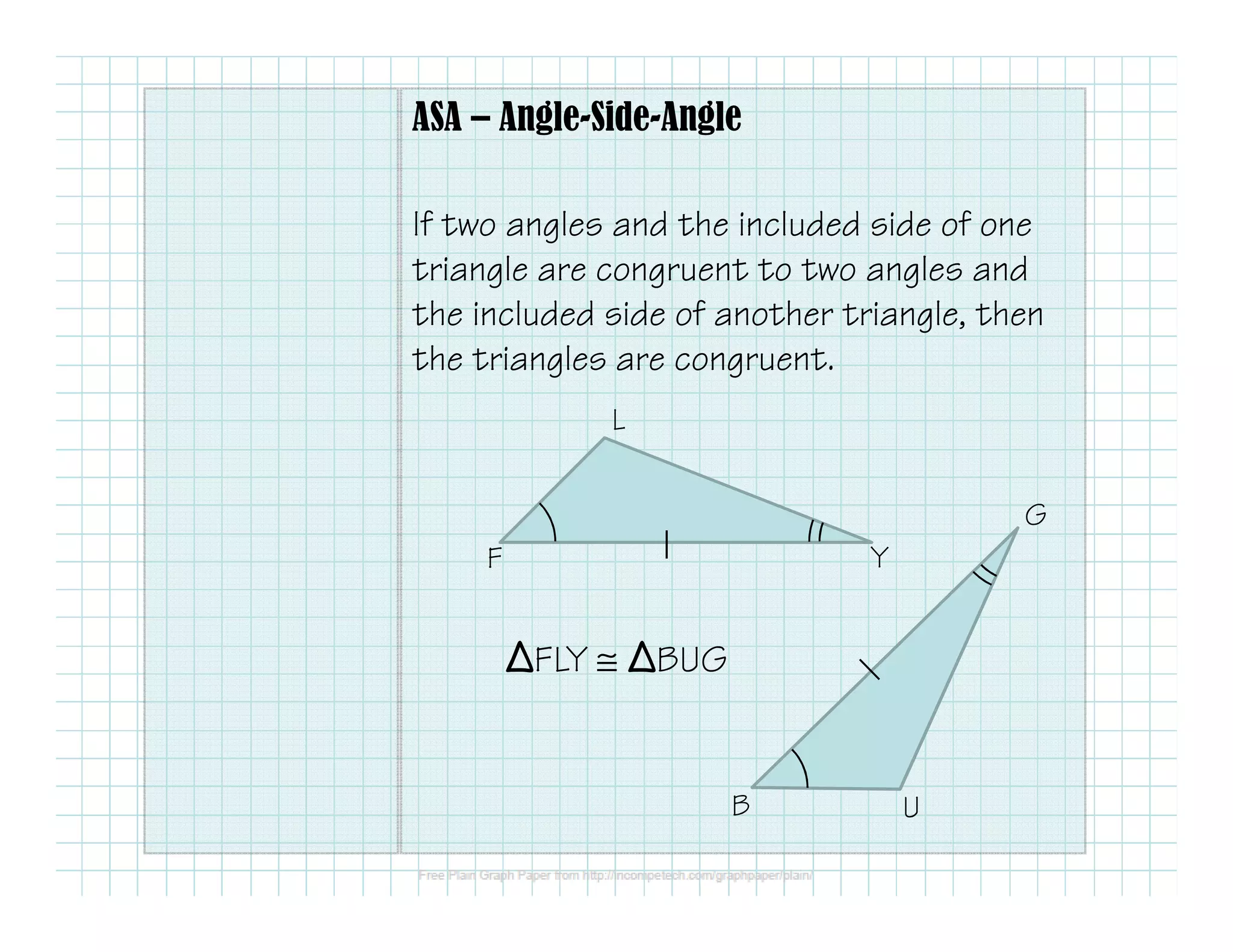
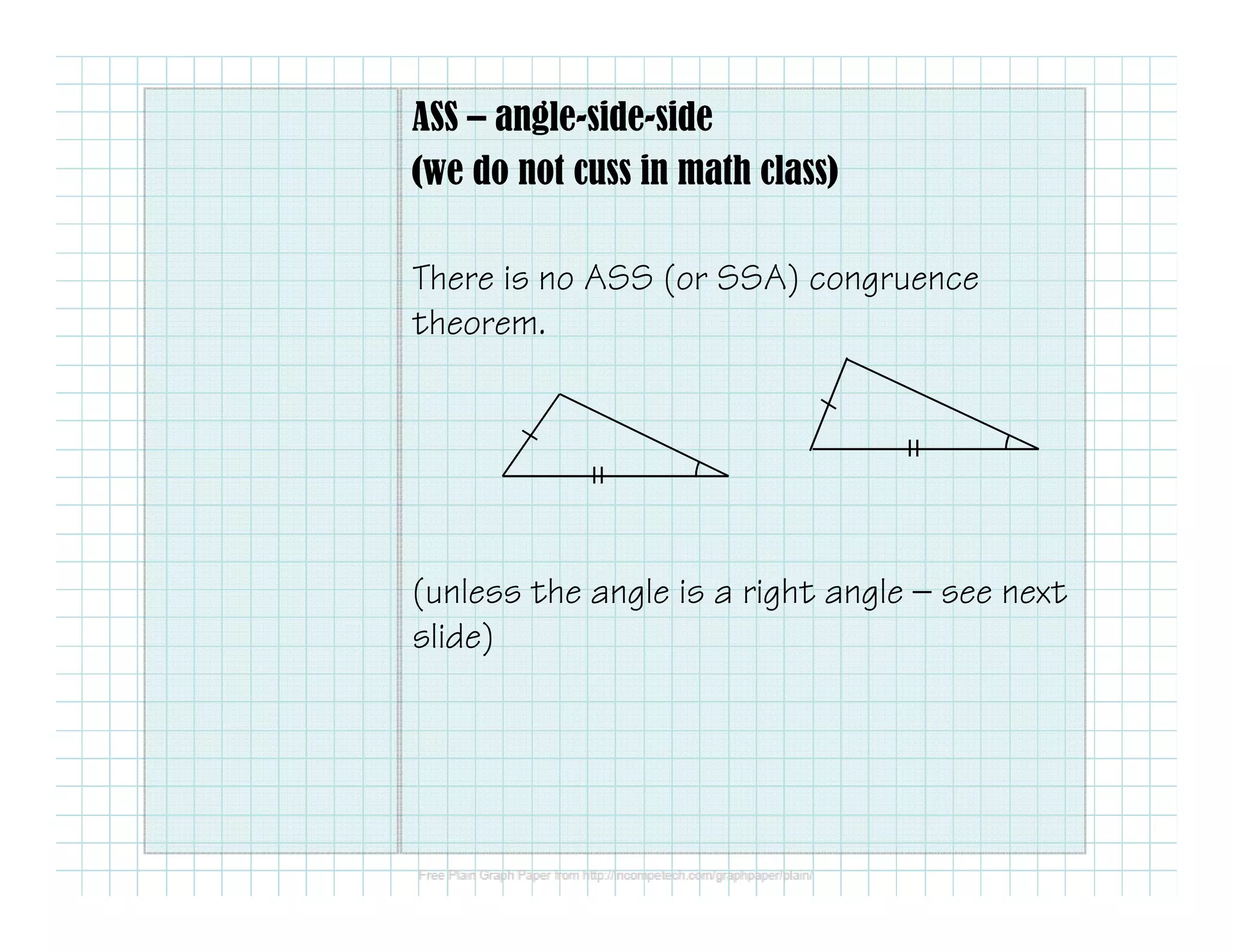
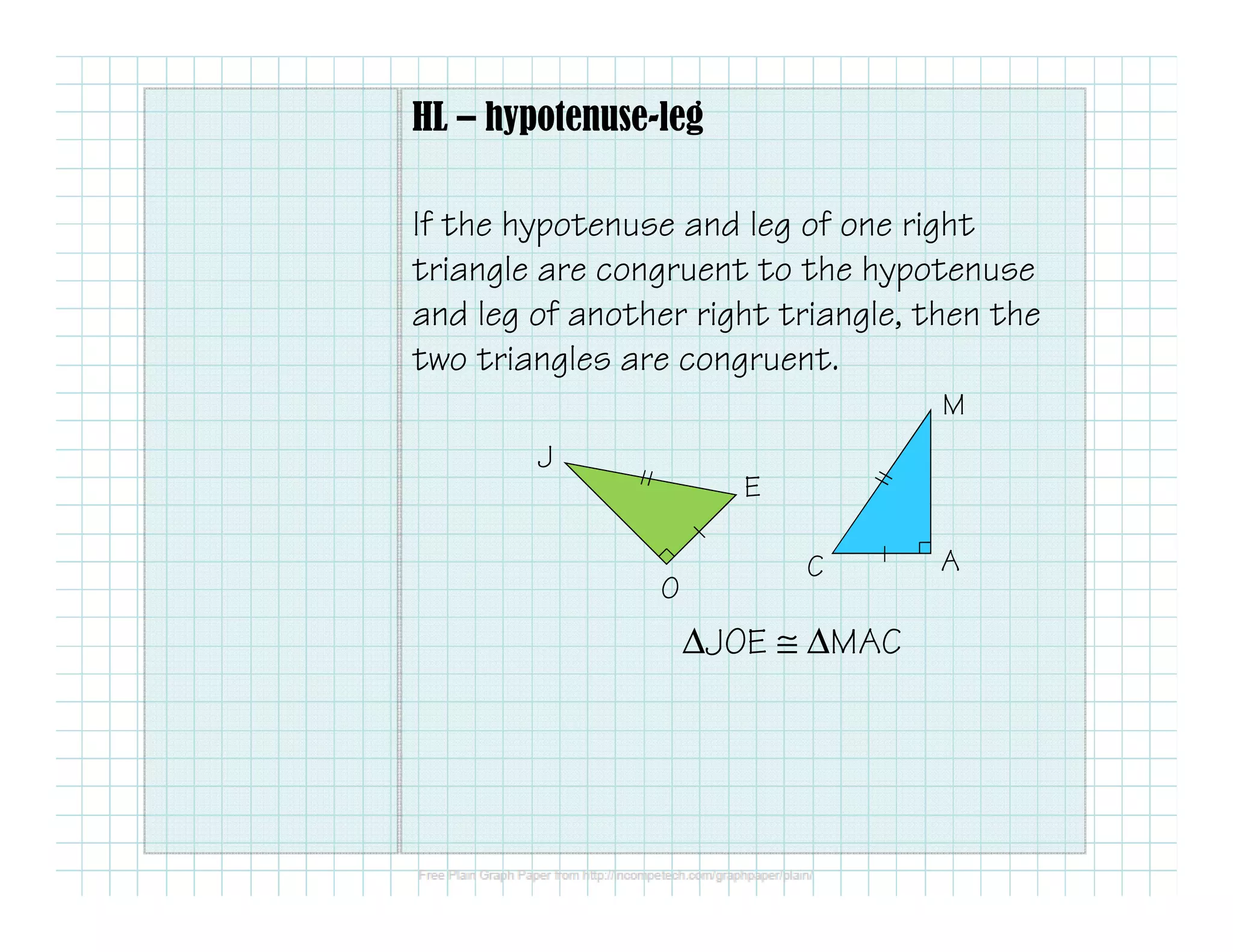
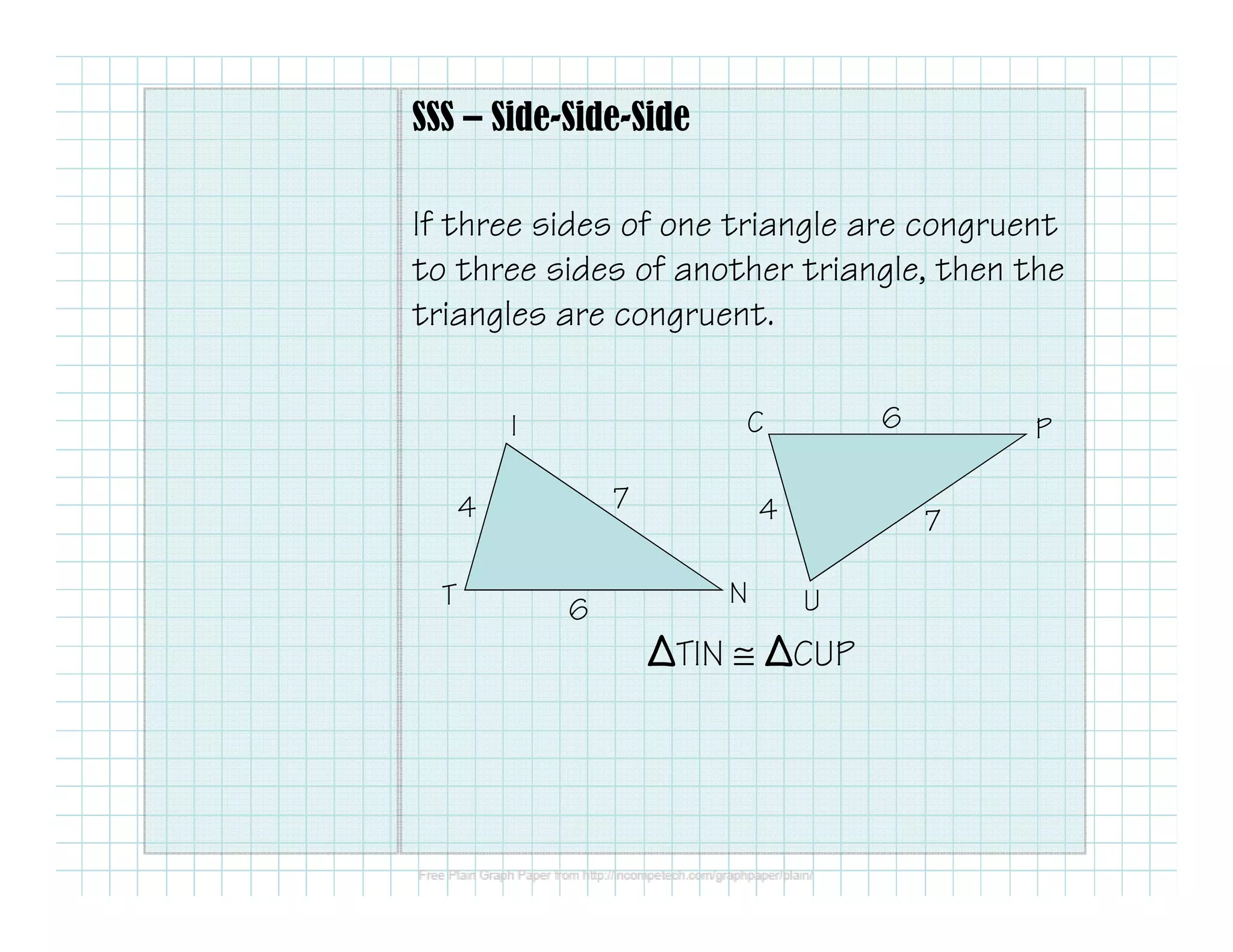
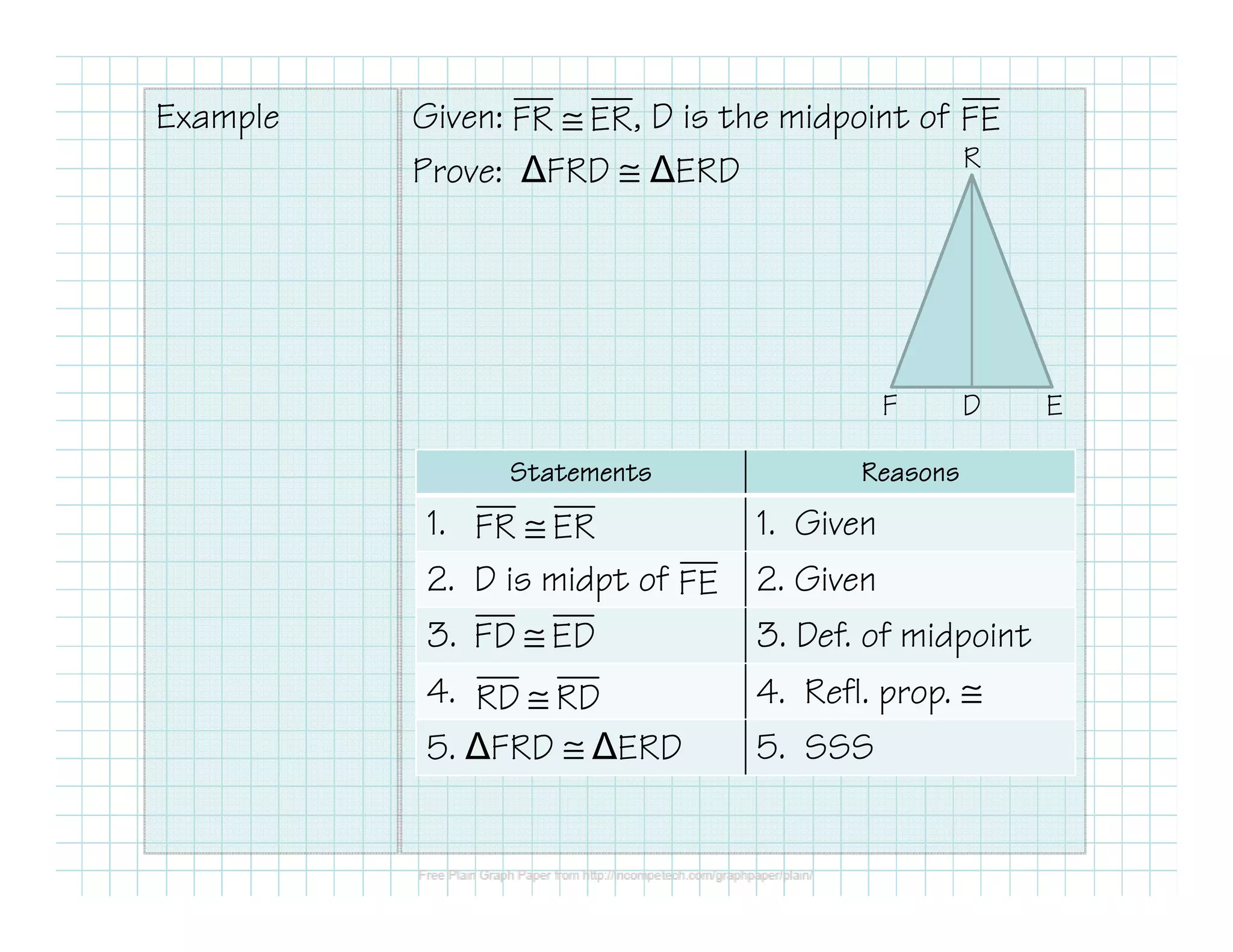
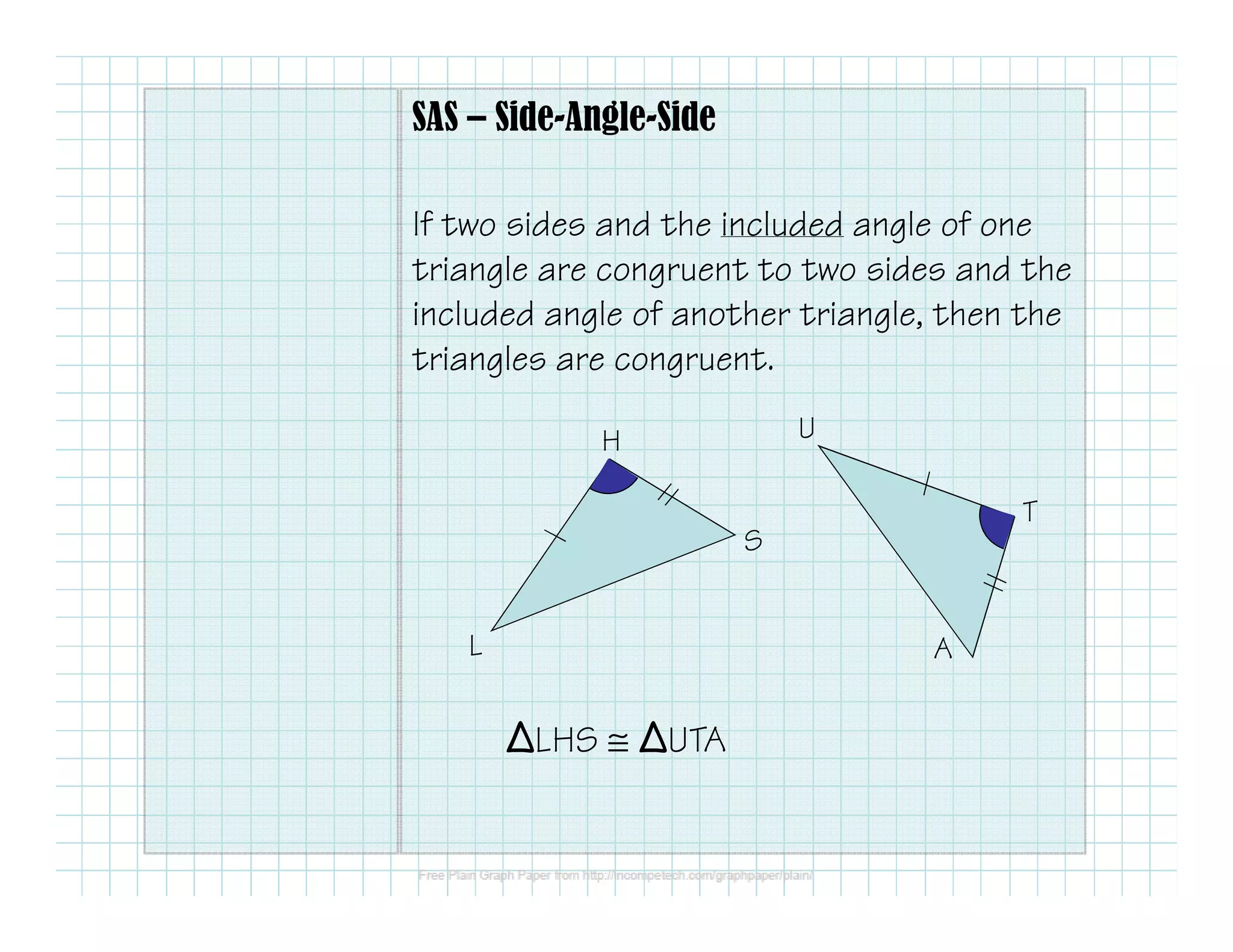
This document outlines different methods for proving that two triangles are congruent: - Side-Side-Side (SSS) - If three sides of one triangle are congruent to three sides of another triangle, then the triangles are congruent. - Side-Angle-Side (SAS) - If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent. - Angle-Side-Angle (ASA) - If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent.

1. Obj. 17 Congruent Triangles
The student is able to (I can):
• Identify congruent parts based on a congruence
relationship statement
• Identify and prove congruent triangles given
— Three pairs of congruent sides (Side-Side-Side)
— Two pairs of congruent sides and a pair of congruent
included angles (Side-Angle-Side)
— Two angles and a side (Angle-Side-Angle and Angle-
Angle-Side)
— A Hypotenuse and a Leg of a right triangle

2. congruent
polygons
Geometric figures are congruent if they are
the same ssssiiiizzzzeeee and sssshhhhaaaappppeeee. Corresponding
angles and corresponding sides are in the
same position in polygons with the same
number of sides.
Two or more polygons whose corresponding
angles and sides are congruent. In a
congruence statement, the order of the
vertices indicates the corresponding parts.
Example: Name the corresponding angles if
polygon SWIM @ polygon ZERO.
ÐS @ ÐZ; ÐW @ ÐE; ÐI @ ÐR; ÐM @ ÐO

3. Example
R P
E D
A
C
Corresponding
Angles
ÐR @ ÐC
ÐE @ ÐP
ÐD @ ÐA
Corresponding
Sides
ED @ PA
RE @ CP
RD @ CA
Thus, RED @ CPA.

4. SSS – Side-Side-Side
If three sides of one triangle are congruent
to three sides of another triangle, then the
triangles are congruent.
T
I
C
N
U
P
4
6
7 4
6
7
TIN @ CUP

5. Example Given: , D is the midpoint of
FR @ ER FE
Prove: FRD @ ERD
F
R
D E
SSSSttttaaaatttteeeemmmmeeeennnnttttssss RRRReeeeaaaassssoooonnnnssss
1. FR @ ER
1. Given
2. D is midpt of FE
2. Given
3. FD @ ED
3. Def. of midpoint
4. RD @ RD
4. Refl. prop. @
5. FRD @ ERD 5. SSS

6. SAS – Side-Angle-Side
If two sides and the included angle of one
triangle are congruent to two sides and the
included angle of another triangle, then the
triangles are congruent.
L
H
S
U
T
A
LHS @ UTA

7. Example Given: , A is the midpoint of
FA @ EA RM
Prove: FAR @ EAM F
R
A
M
E
SSSSttttaaaatttteeeemmmmeeeennnnttttssss RRRReeeeaaaassssoooonnnnssss
1. FA @ EA
1. Given
2. ÐFAR @ ÐEAM 2. Vertical Ðs
3. A is midpt of RM
3. Given
4. RA @MA
4. Def. of midpoint
5. FAR @ EAM 5. SAS

8. ASA – Angle-Side-Angle
If two angles and the included side of one
triangle are congruent to two angles and
the included side of another triangle, then
the triangles are congruent.
F
L
Y
B U
G
FLY @ BUG

9. AAS – angle-angle-side
If two angles and a nnnnoooonnnn-iiiinnnncccclllluuuuddddeeeedddd side of one
triangle are congruent to two angles and a
non-included corresponding side of another
triangle, then the triangles are congruent.
I
N
W
Y
O U
DYOU @ DWIN
The non-included sides mmmmuuuusssstttt be
corresponding in order for the triangles to
be congruent.

10. ASS – angle-side-side
(we do not cuss in math class)
There is no ASS (or SSA) congruence
theorem.
(unless the angle is a right angle — see next
slide)

11. HL – hypotenuse-leg
If the hypotenuse and leg of one right
triangle are congruent to the hypotenuse
and leg of another right triangle, then the
two triangles are congruent.
J
O
E
M
C A
DJOE @ DMAC