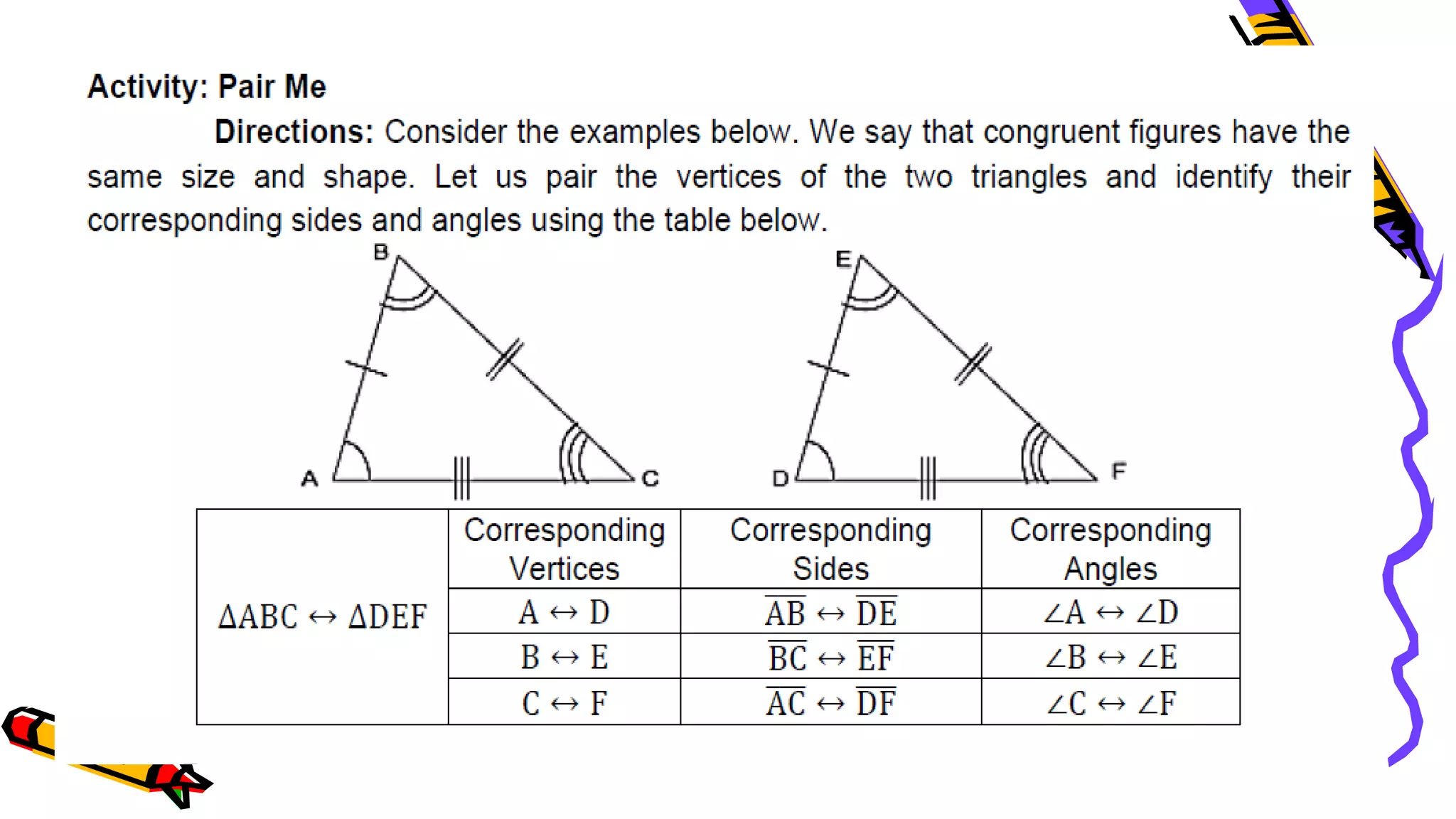
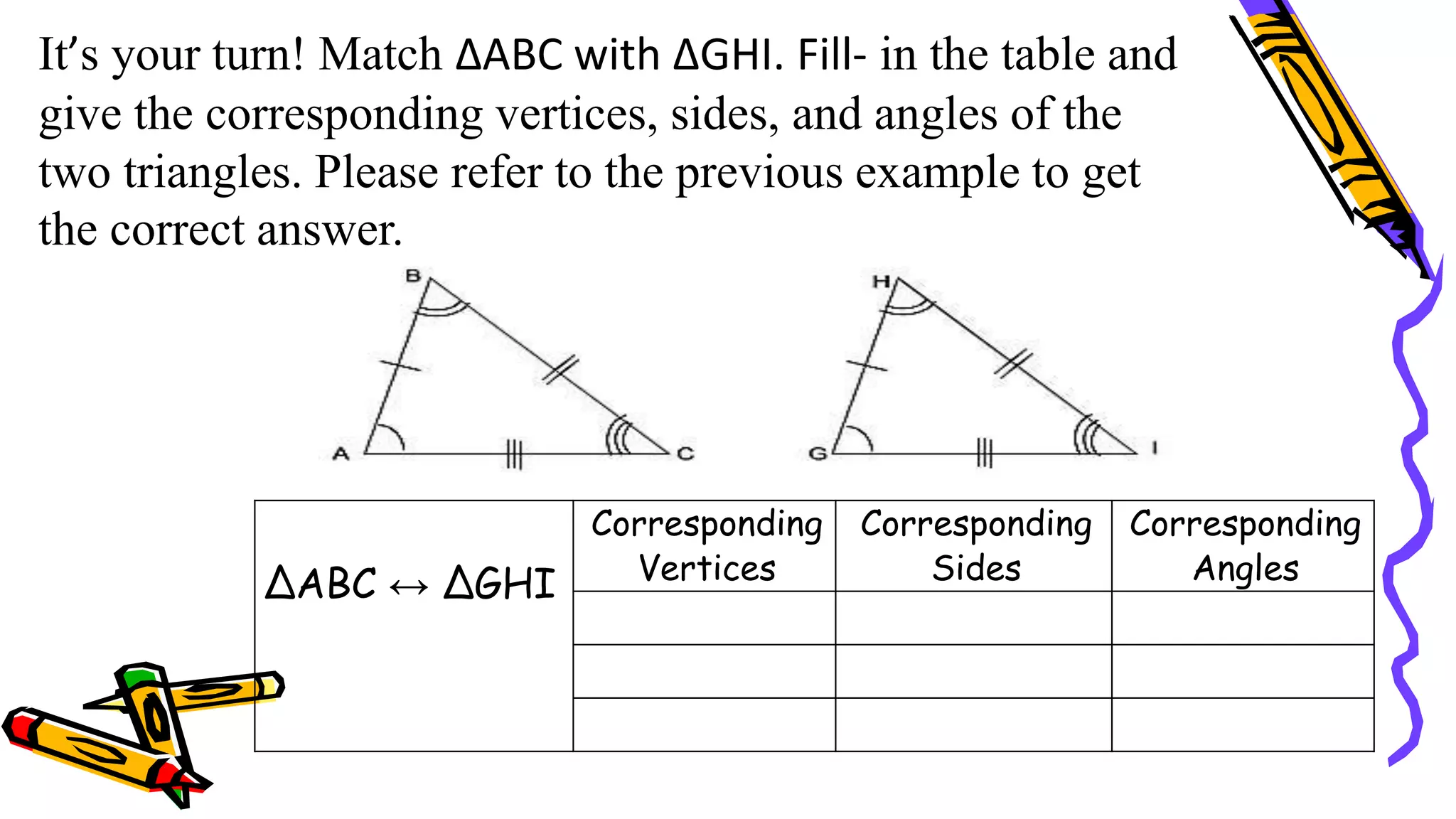
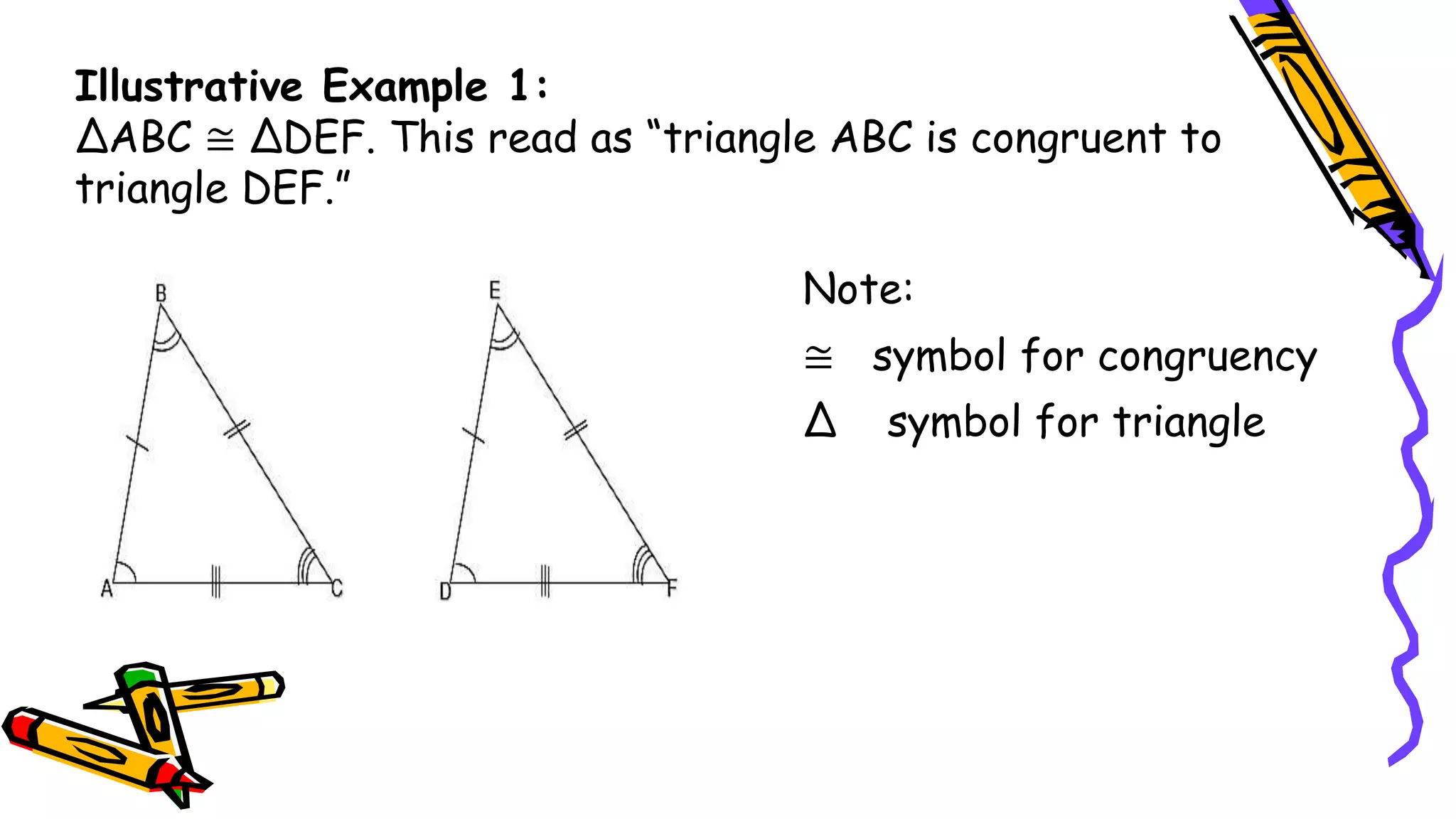
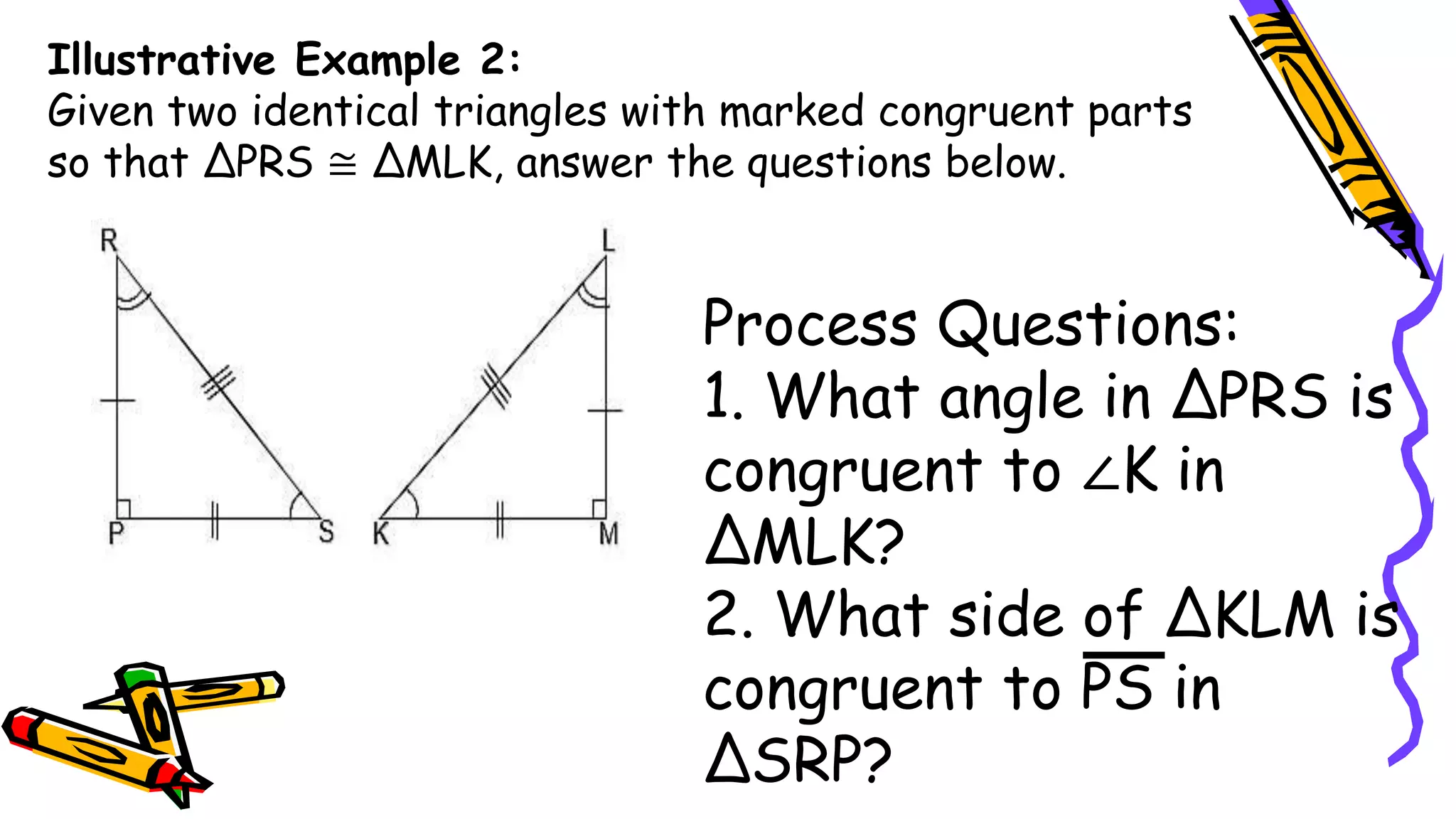
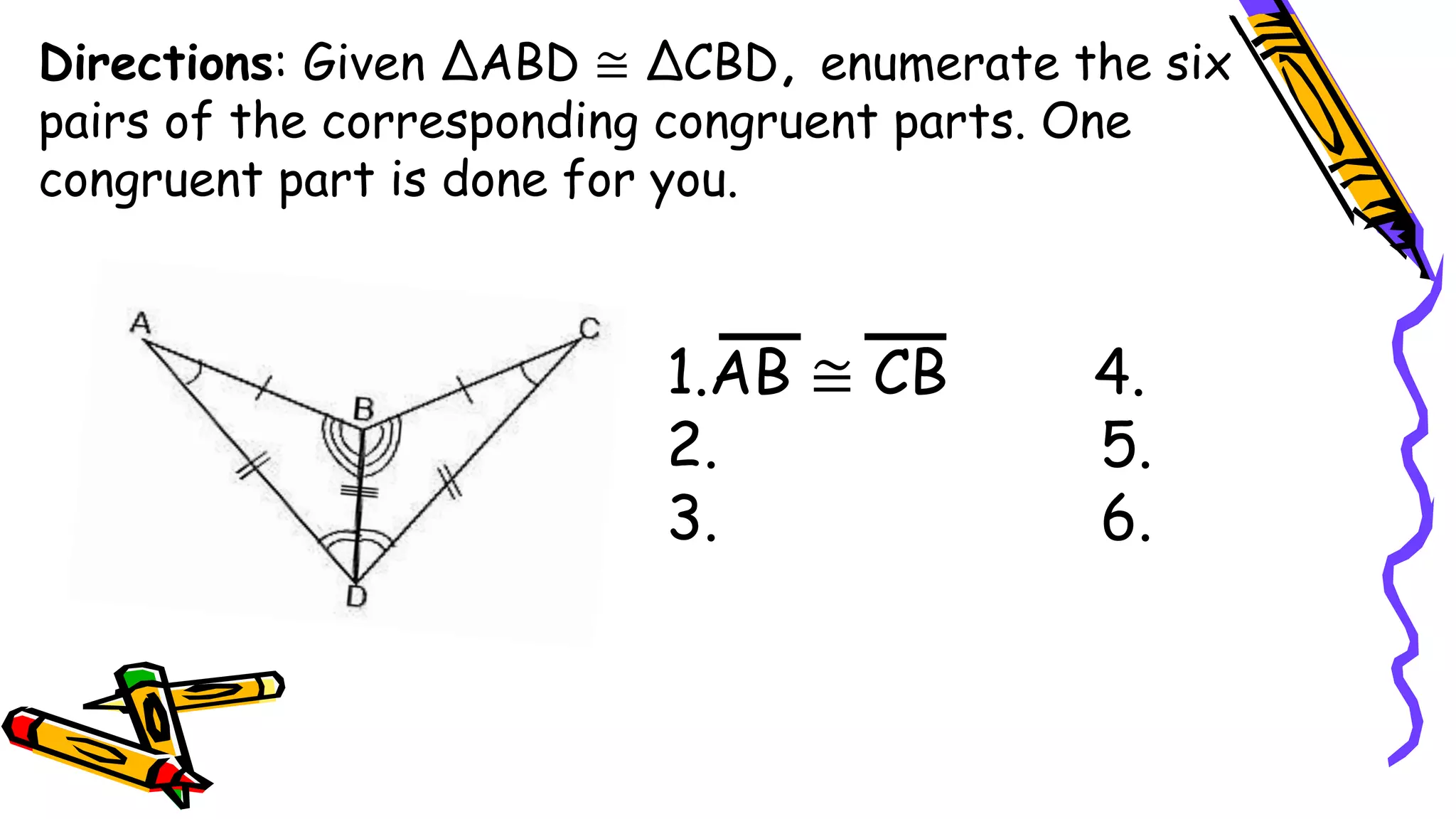
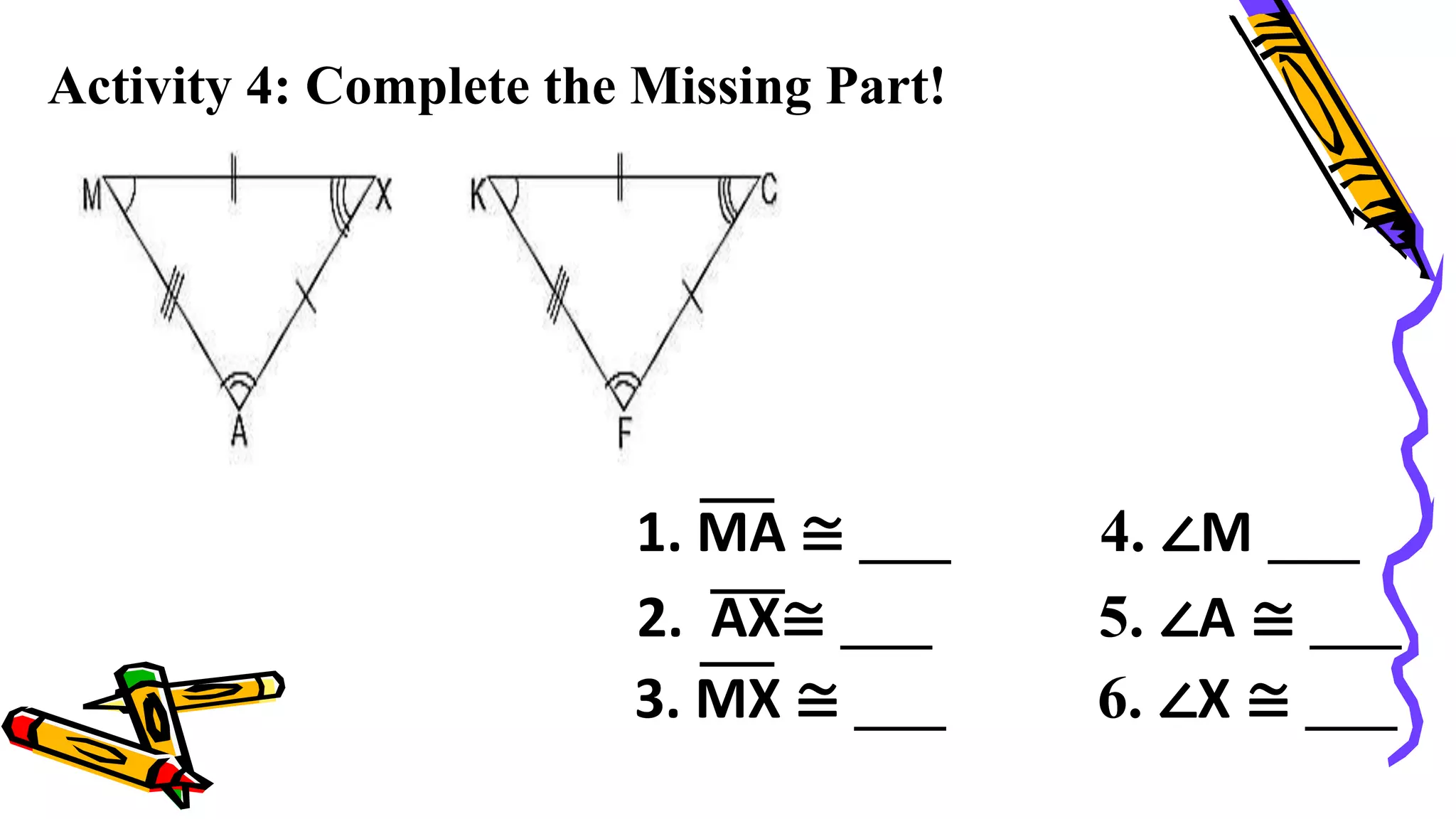
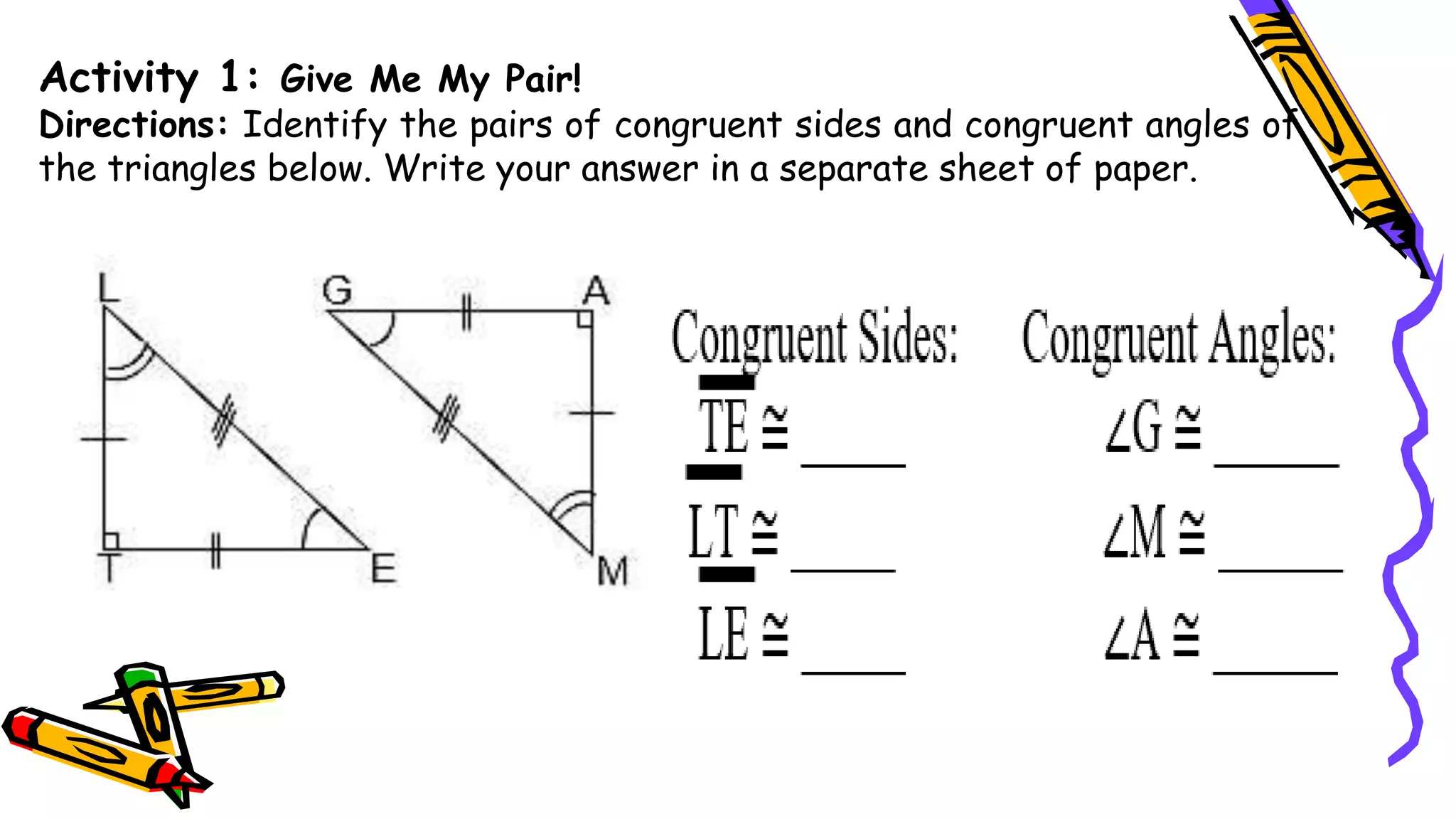
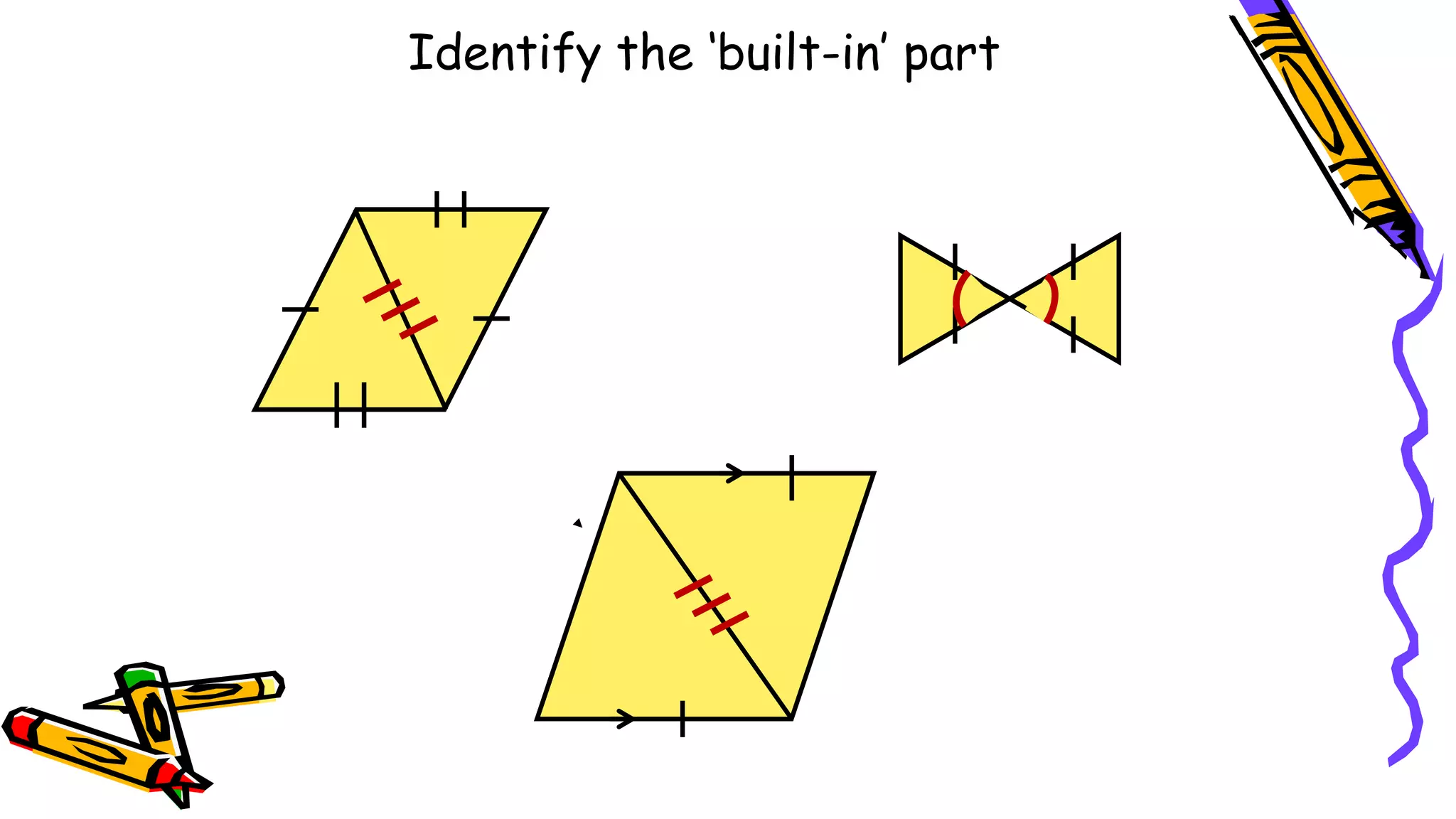
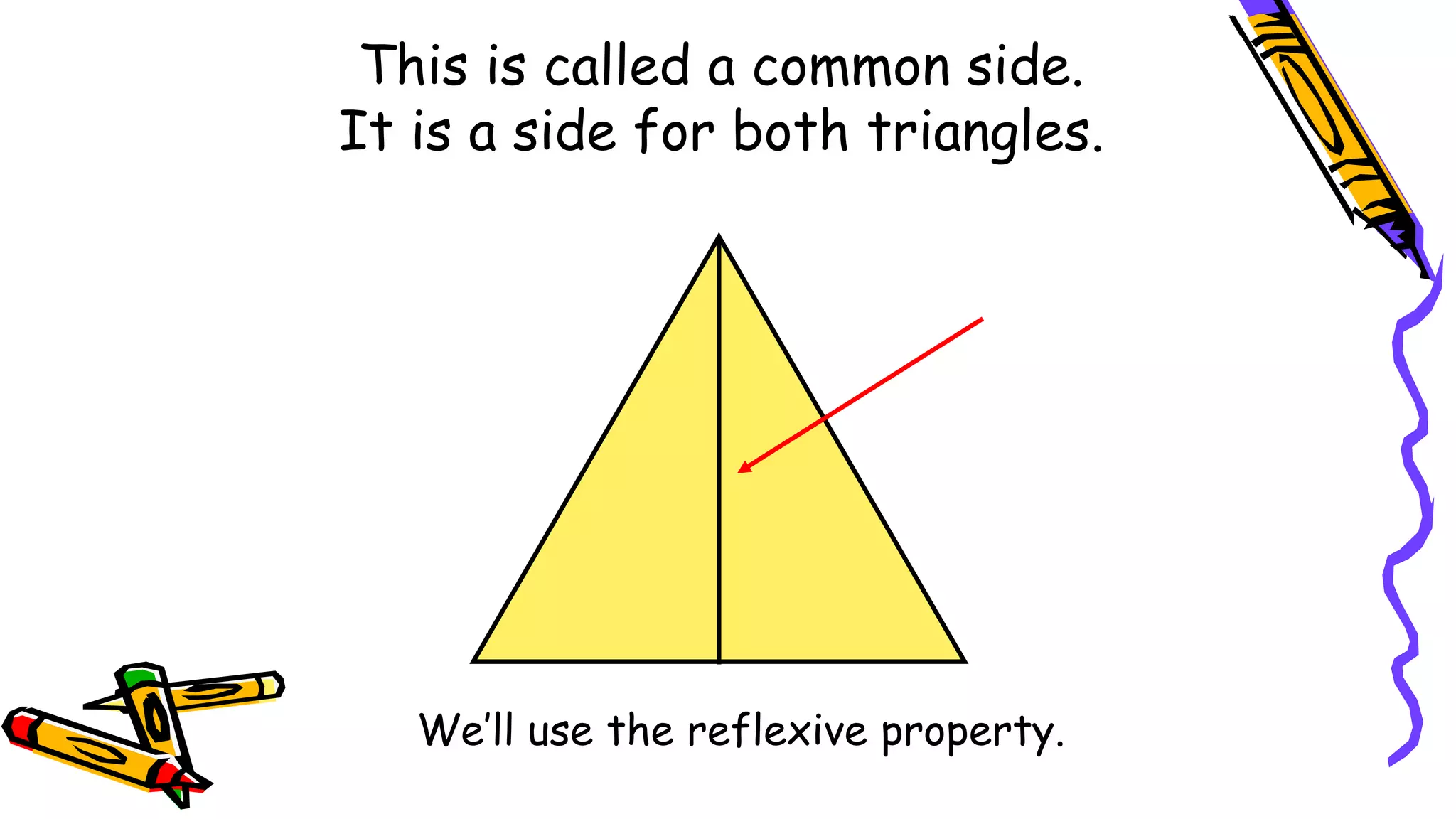
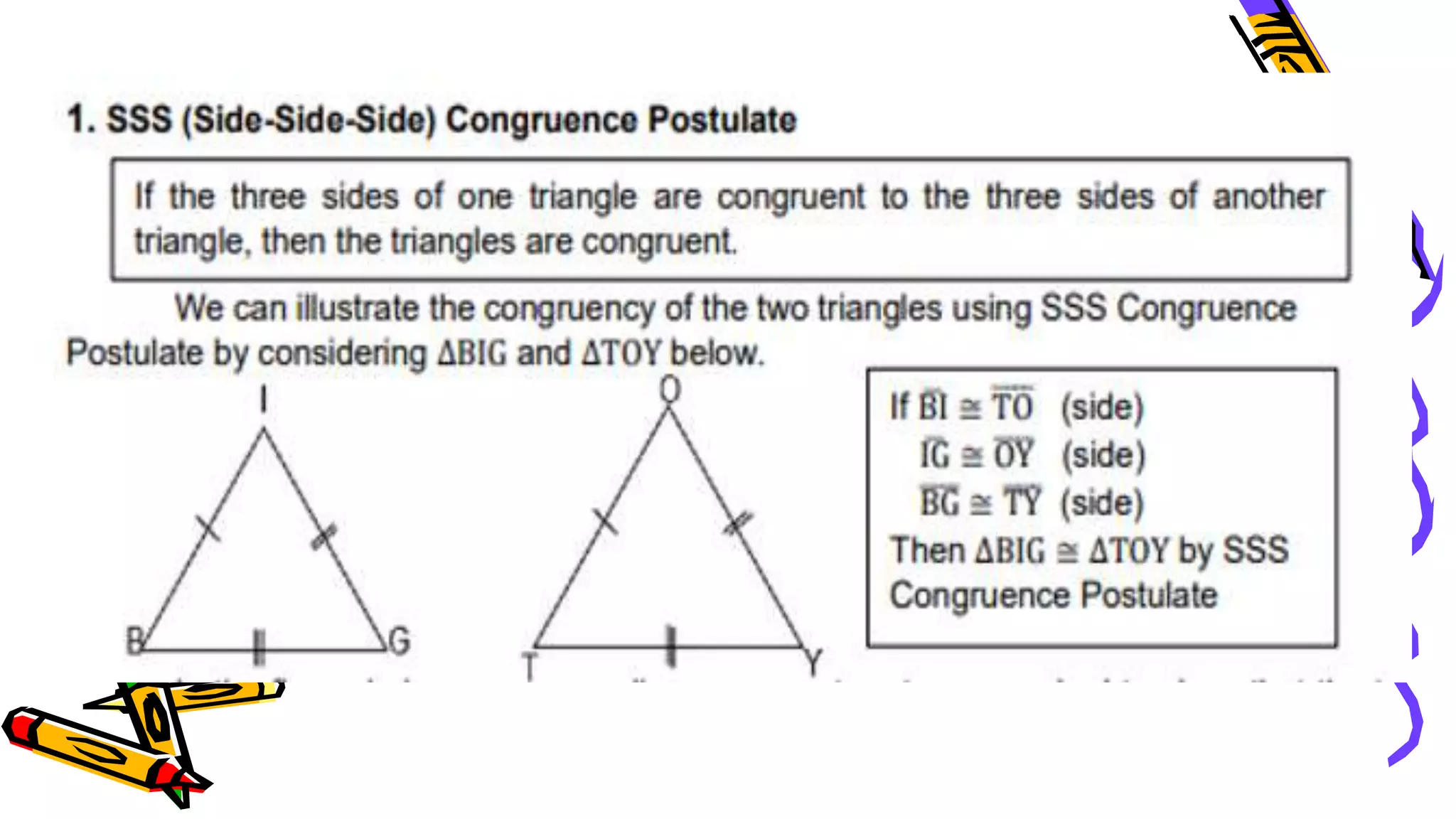
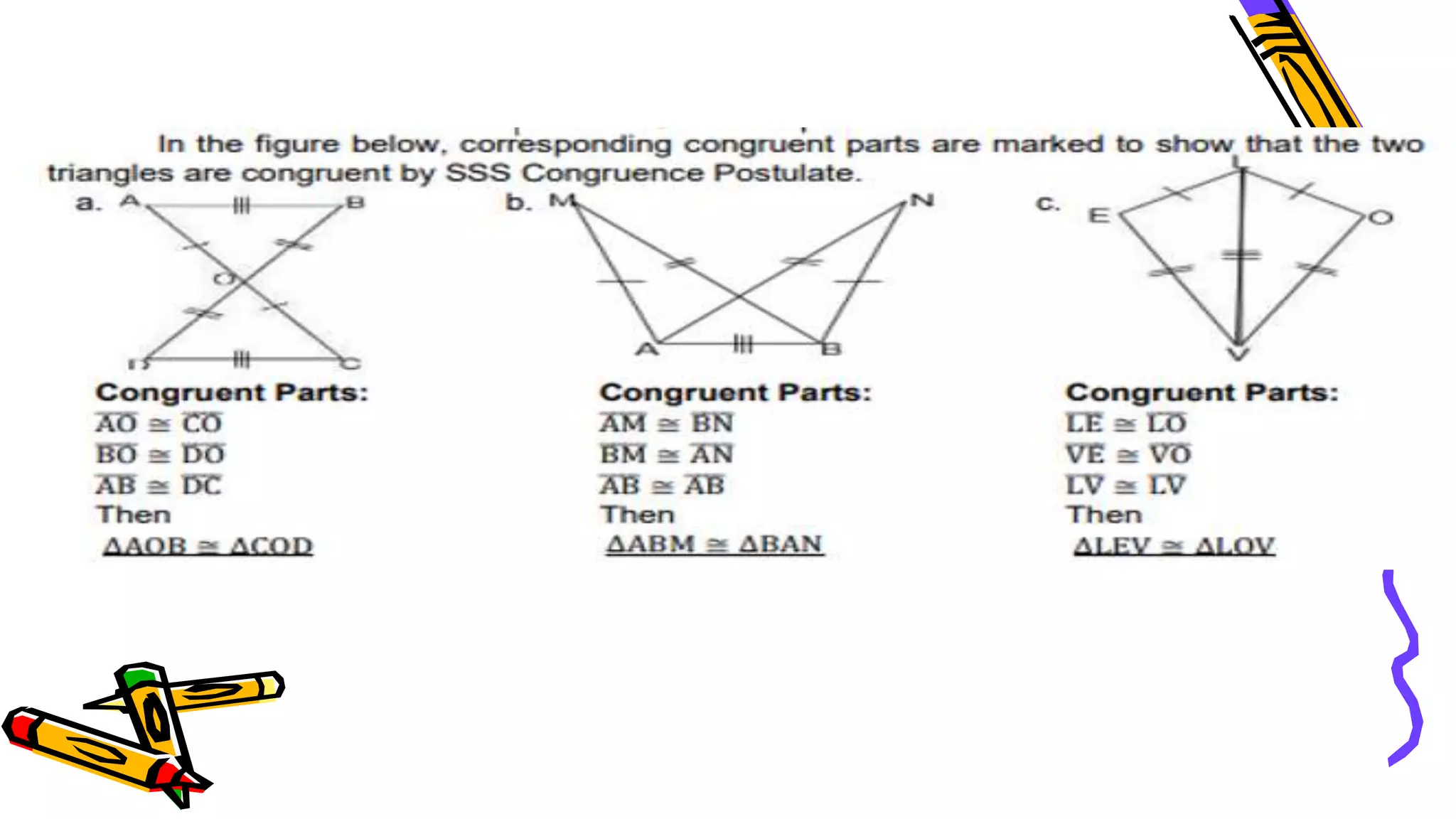
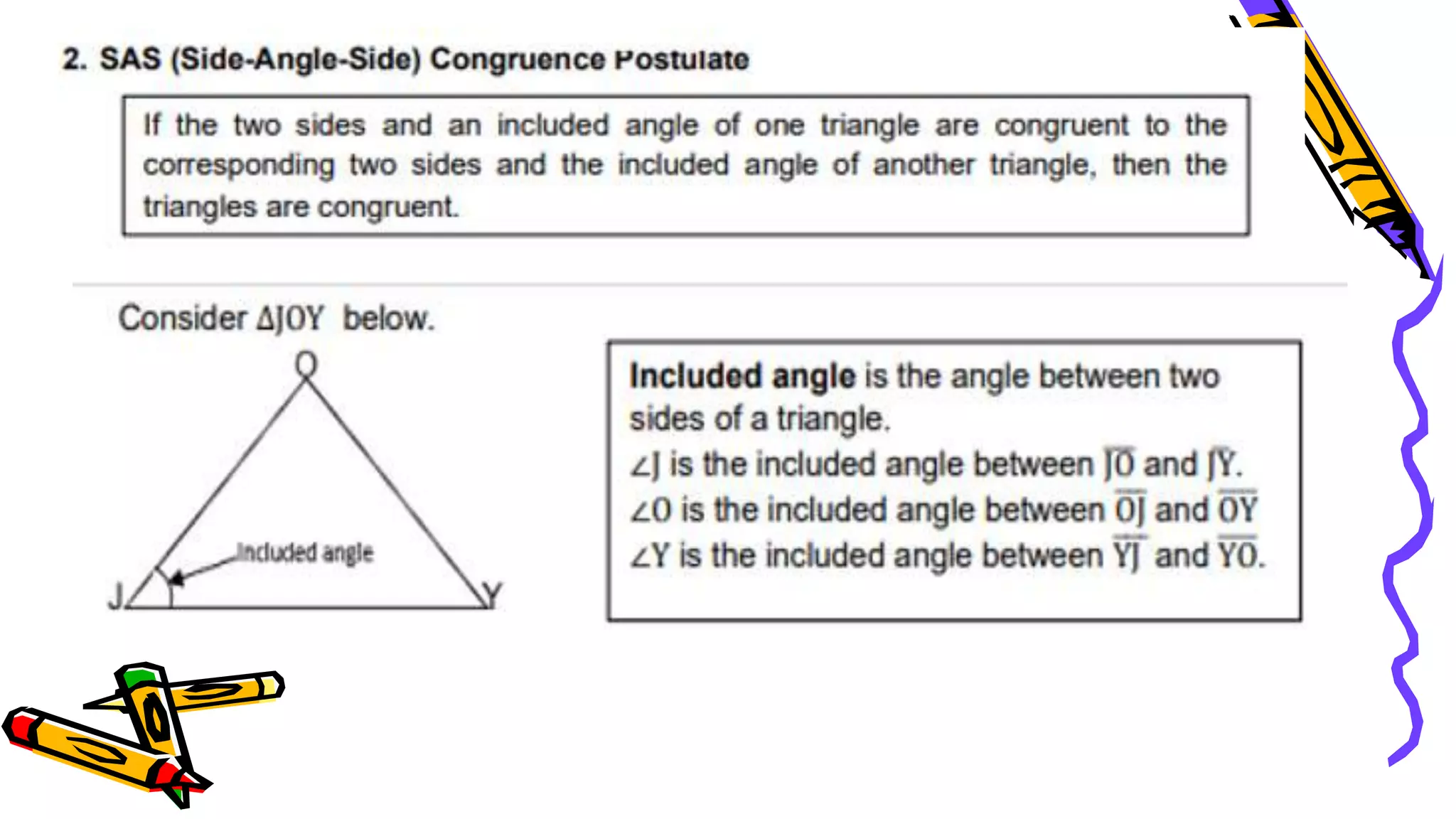
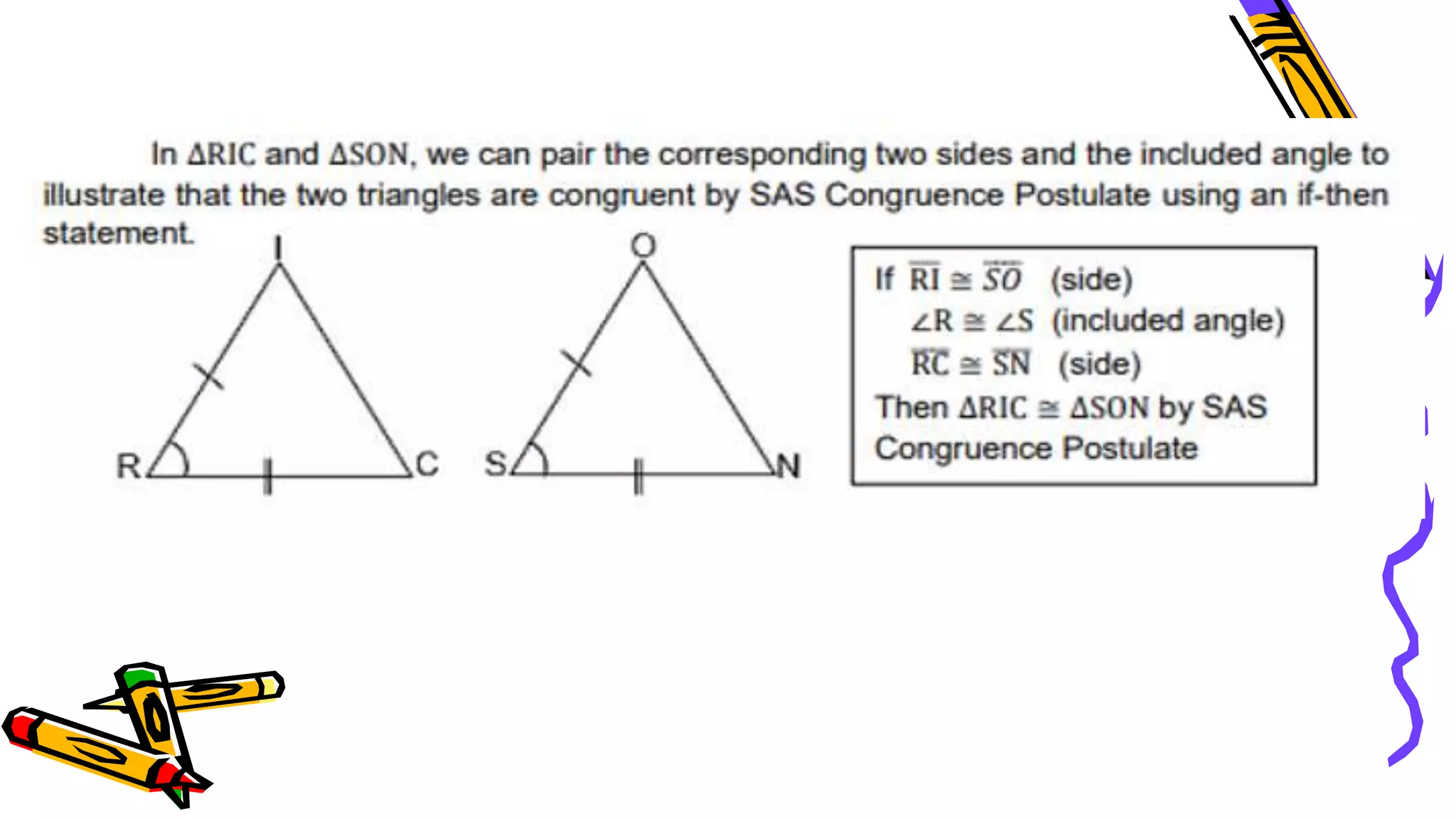
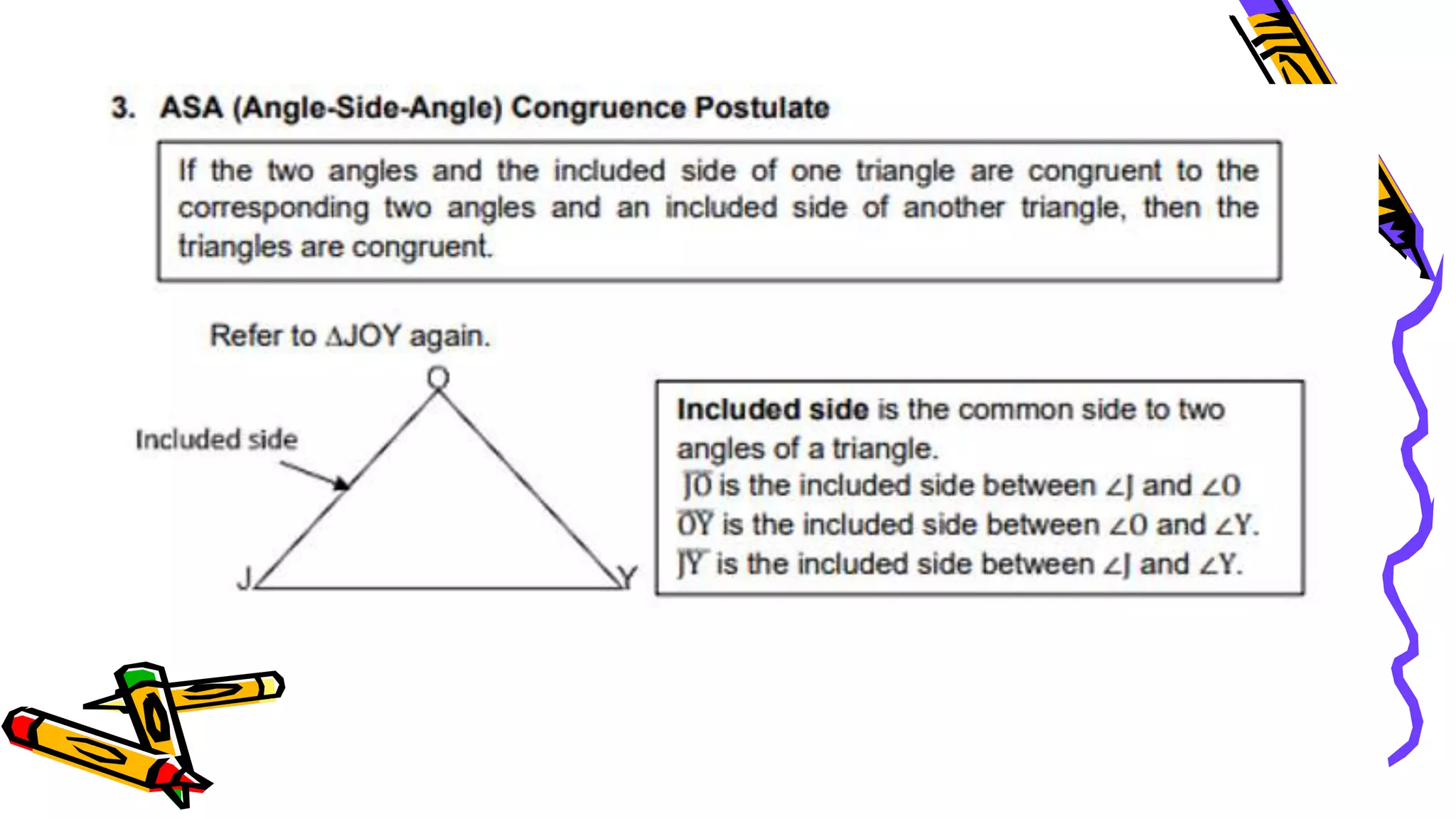
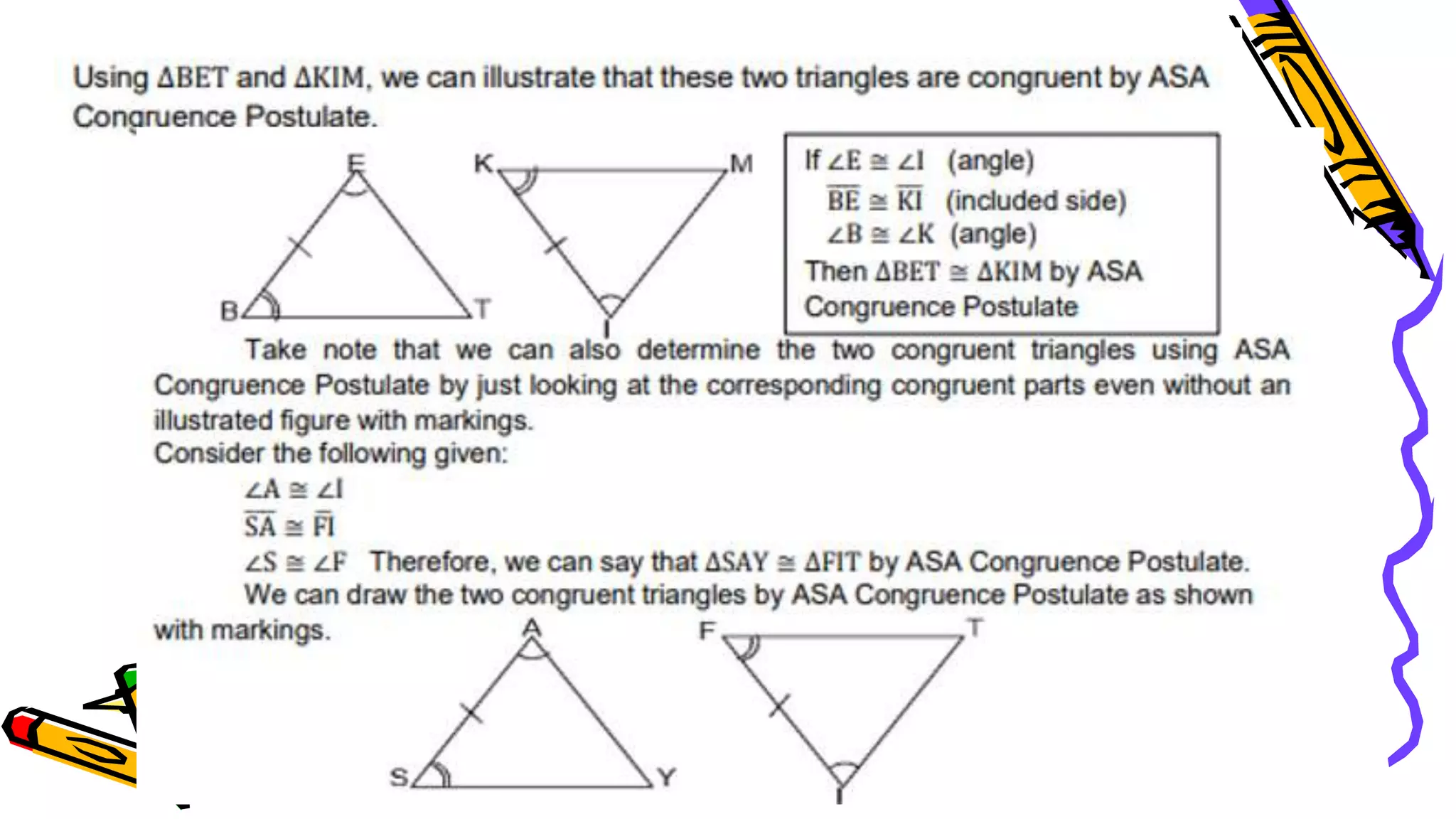
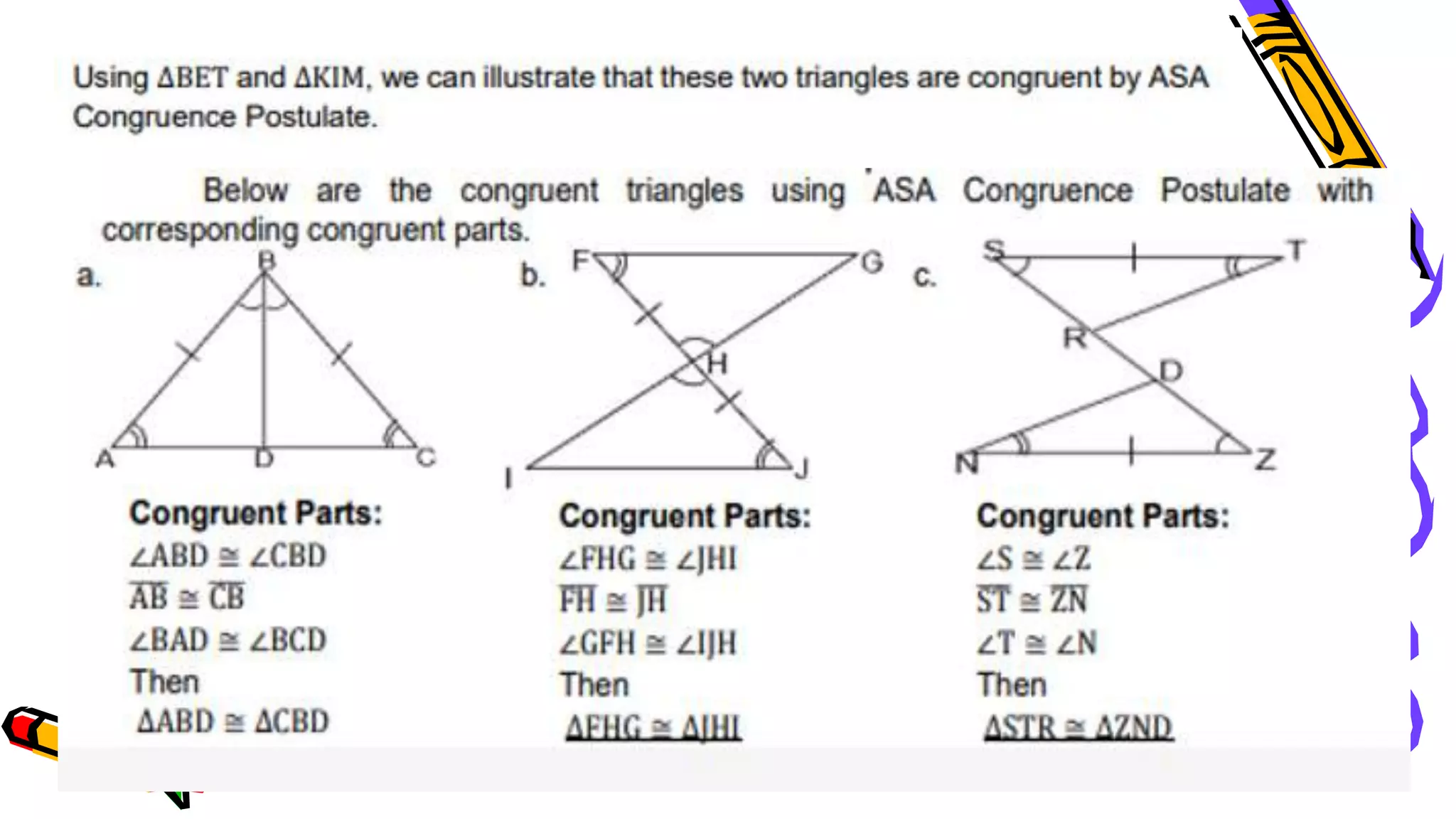
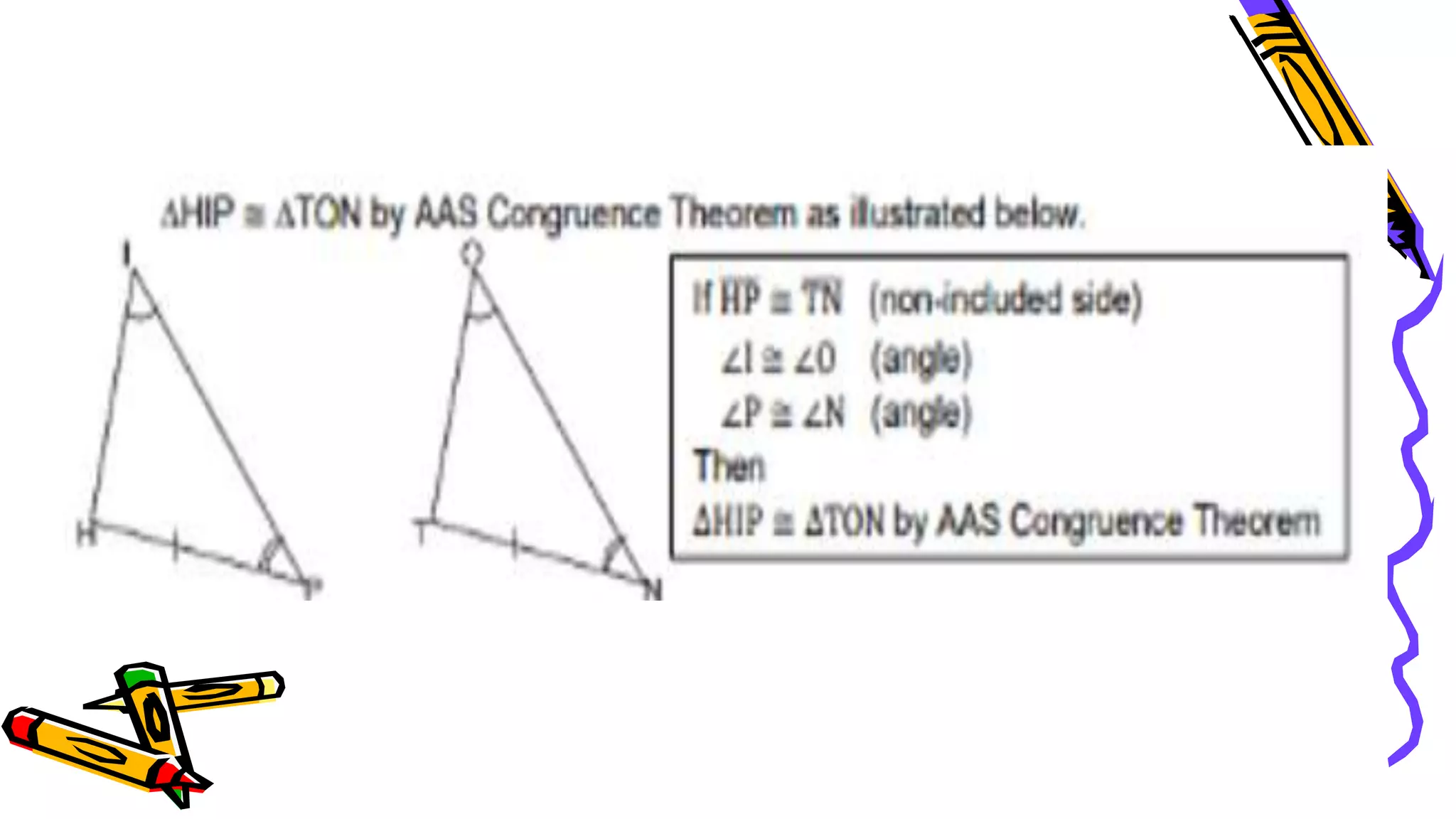
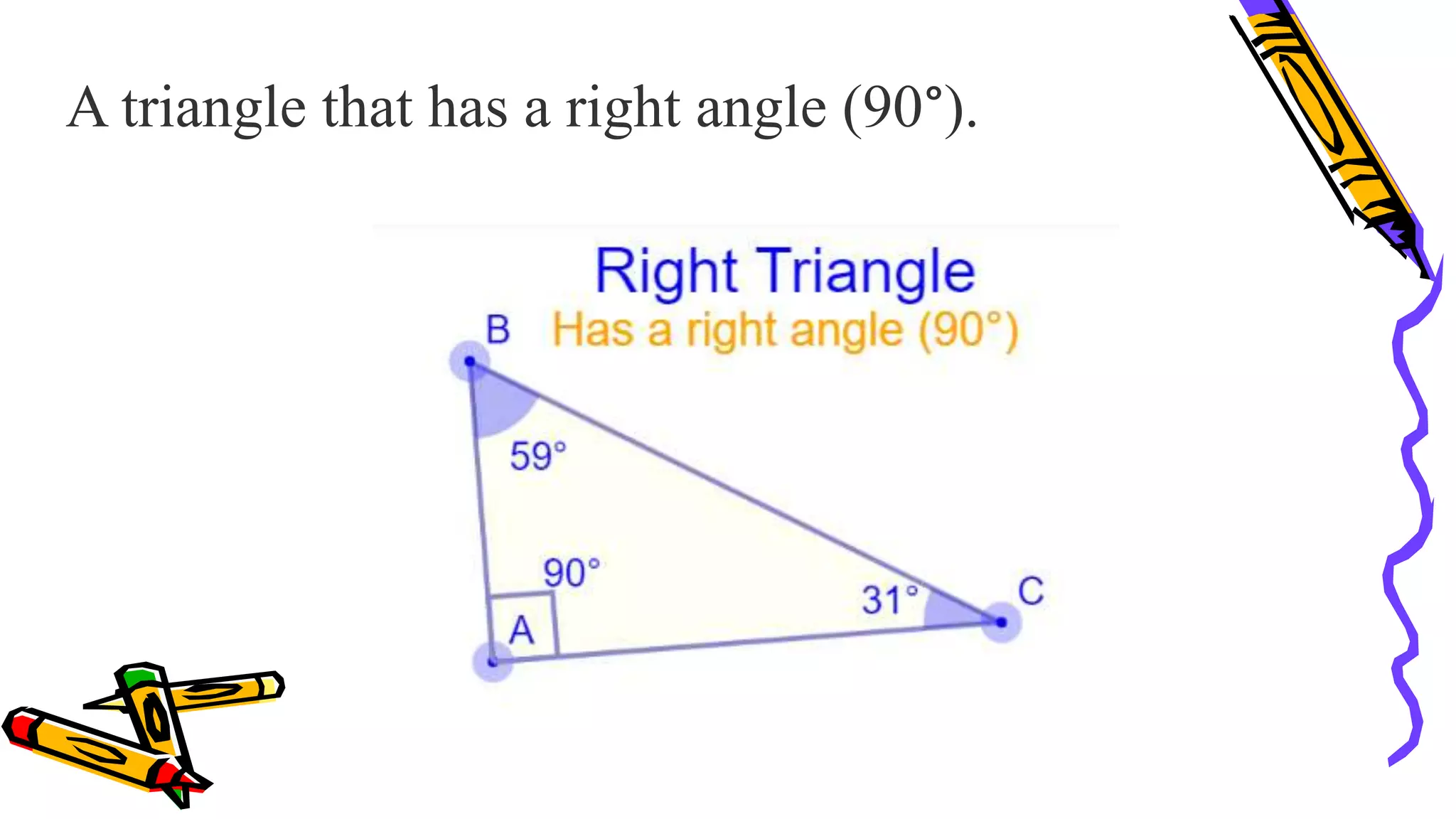
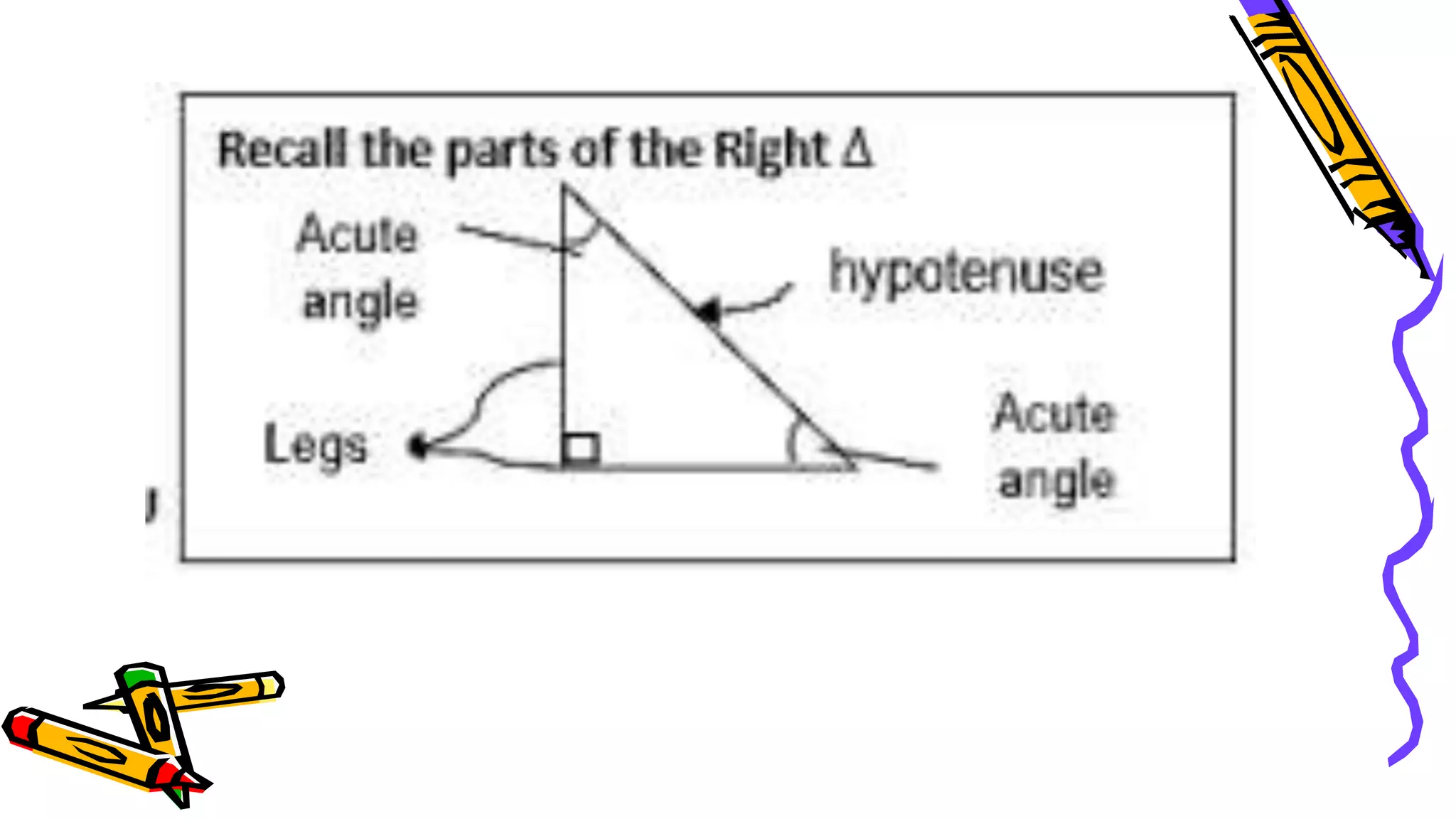
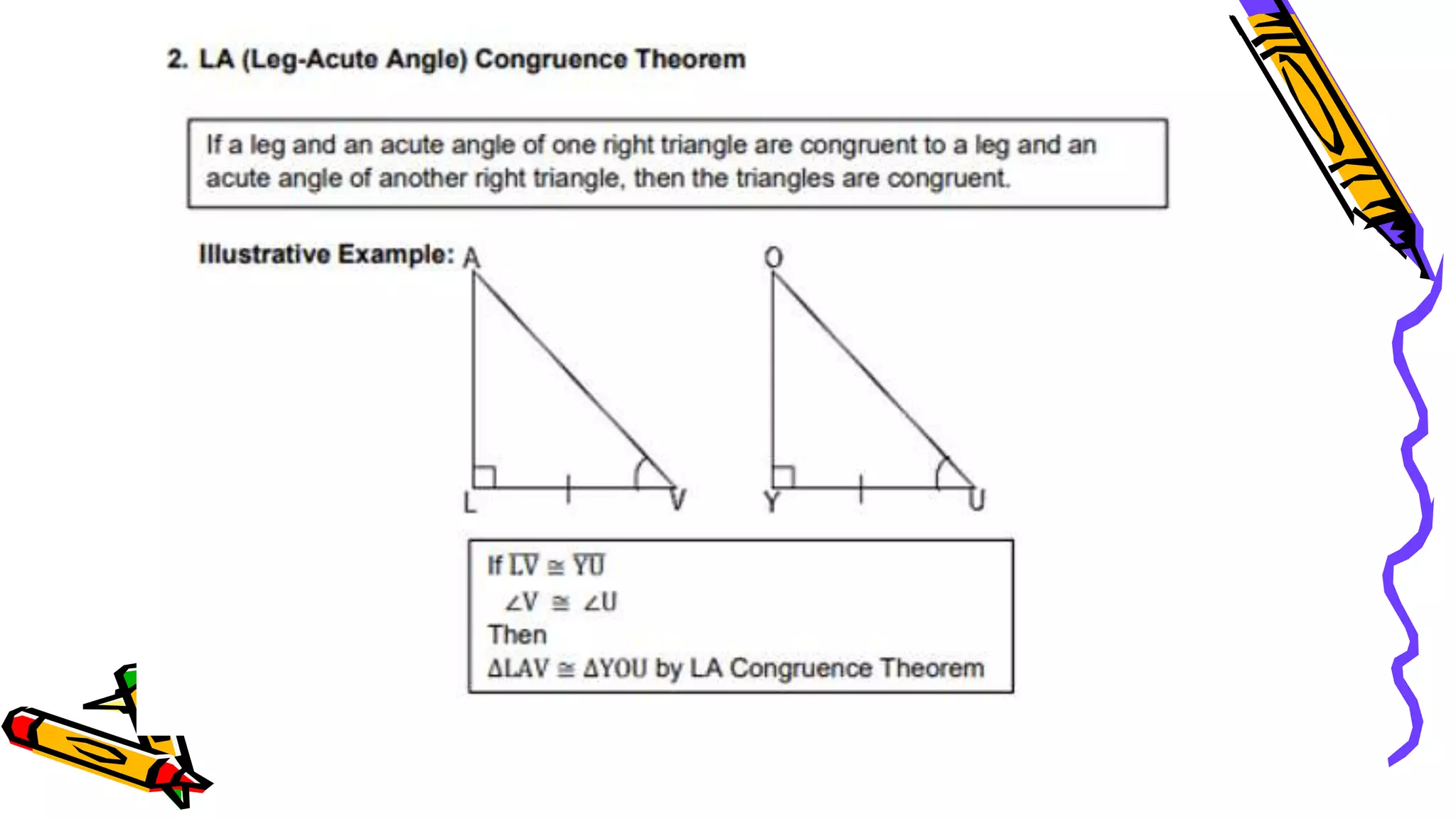
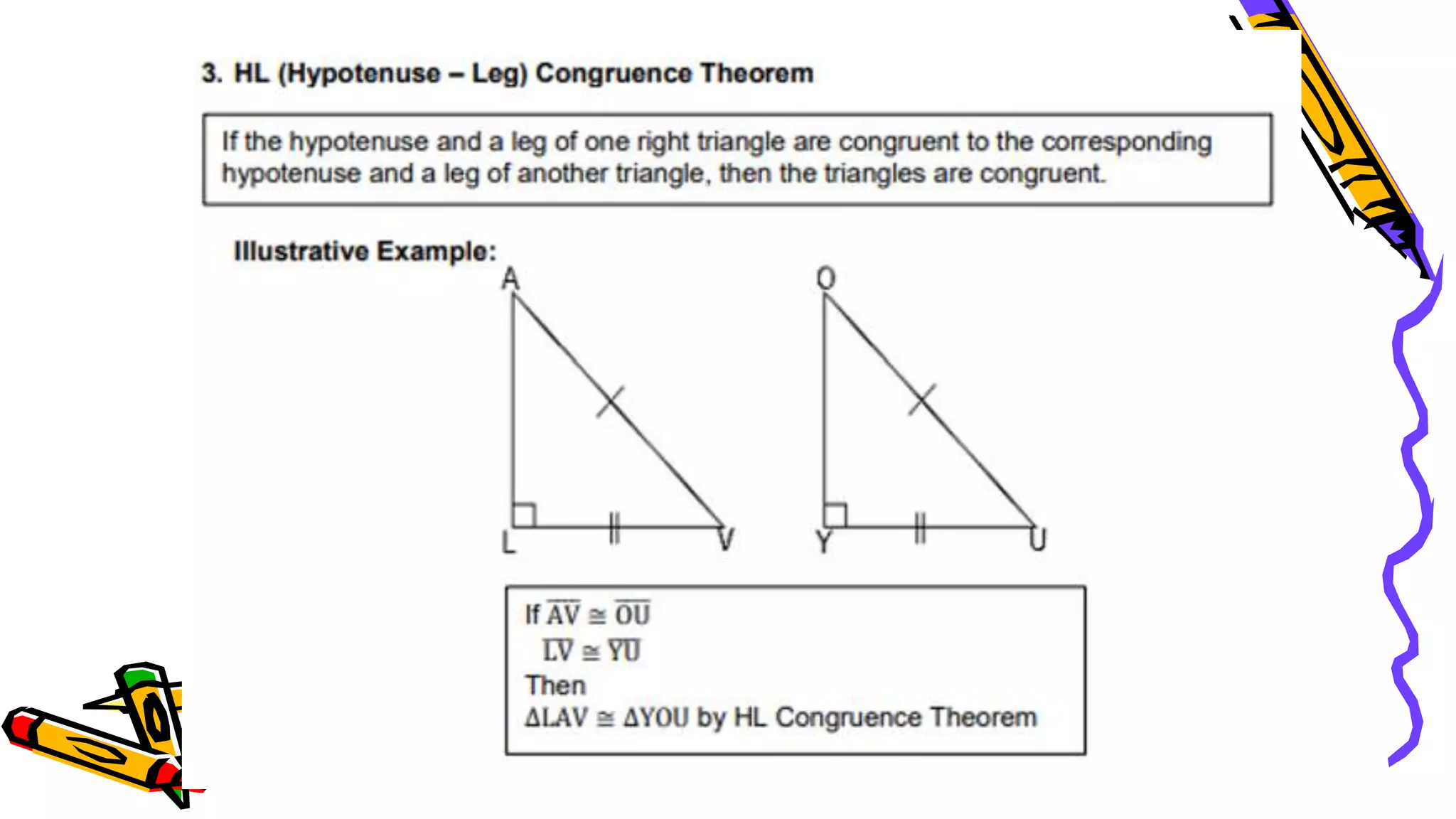
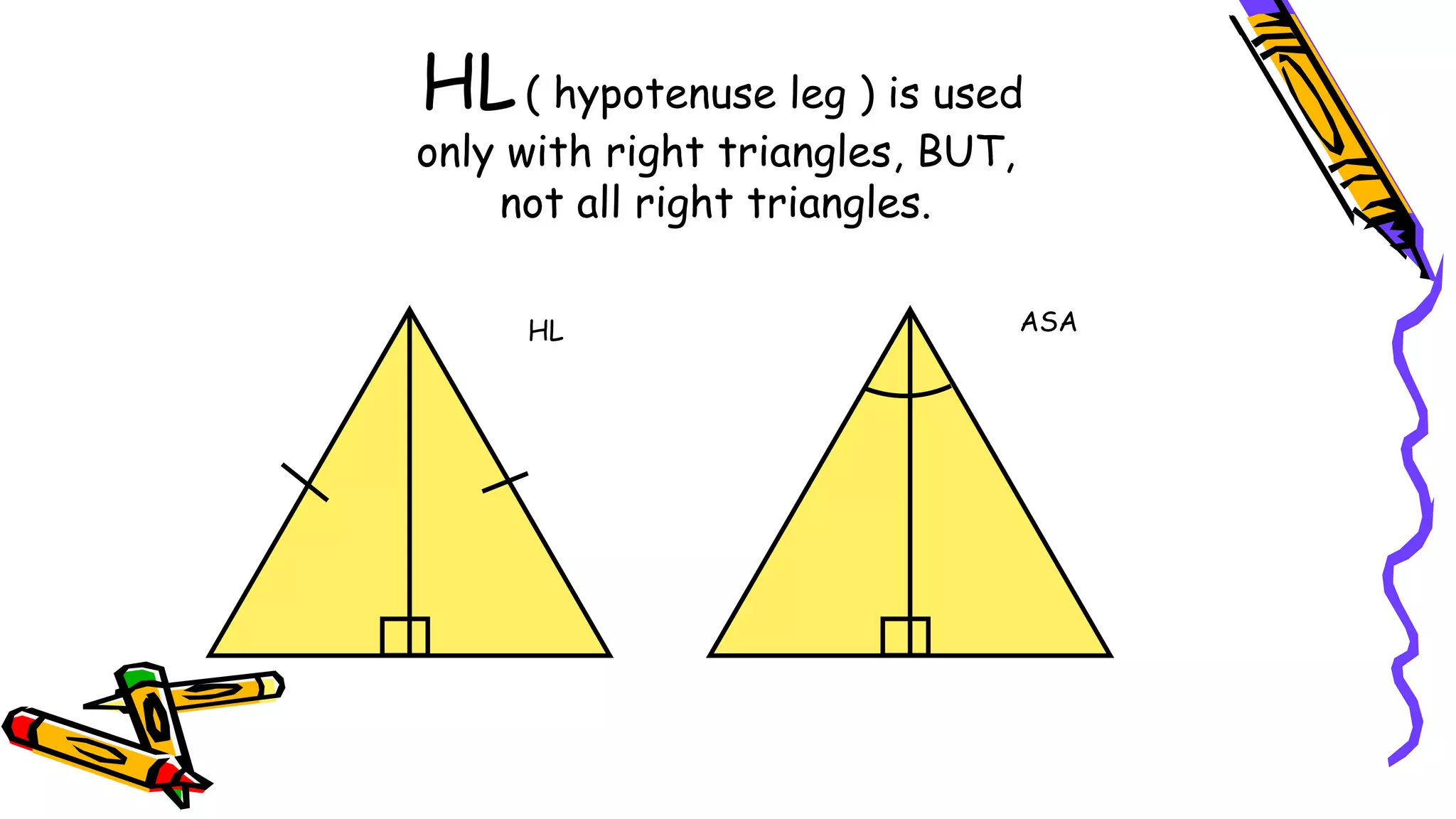
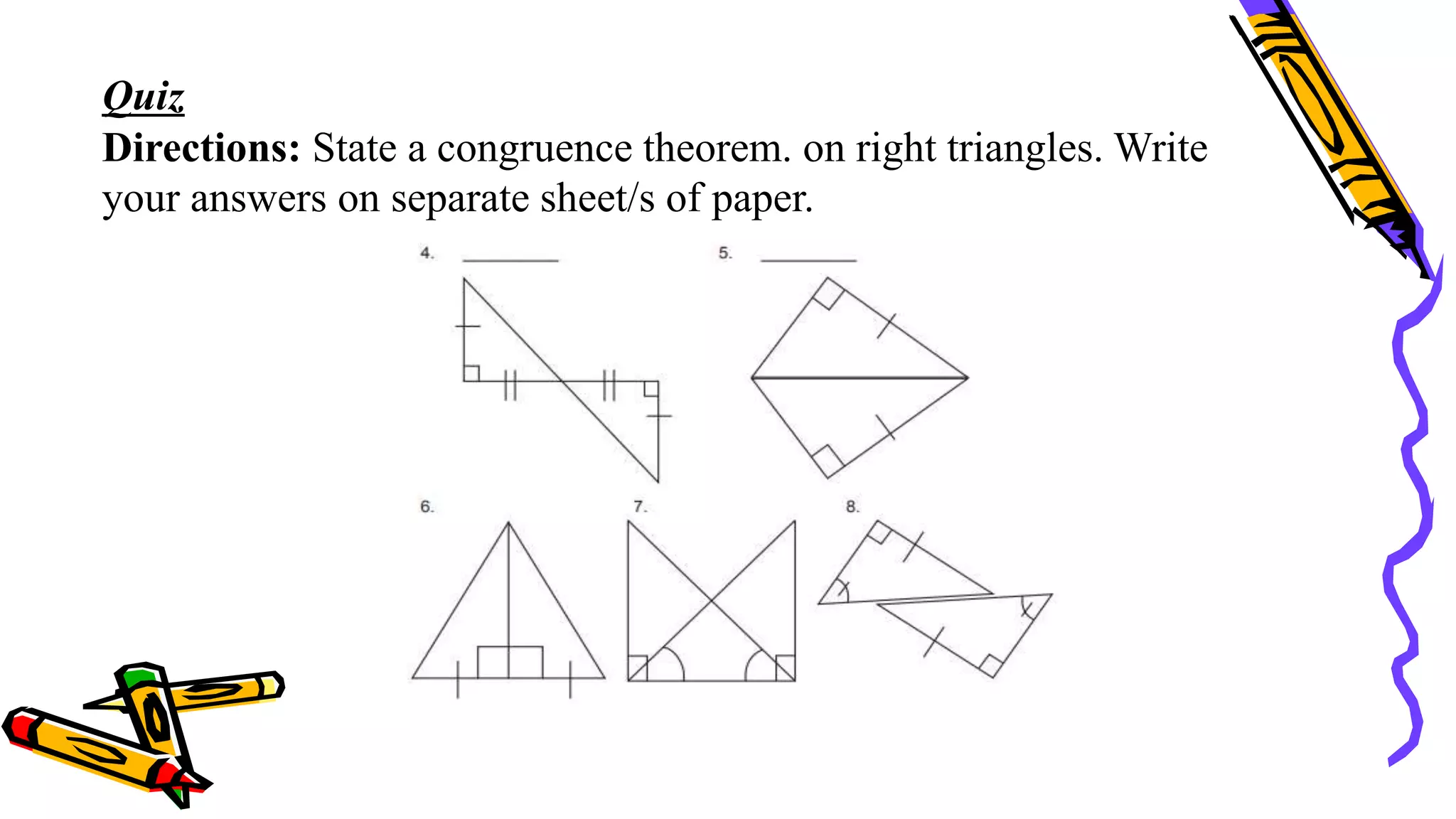
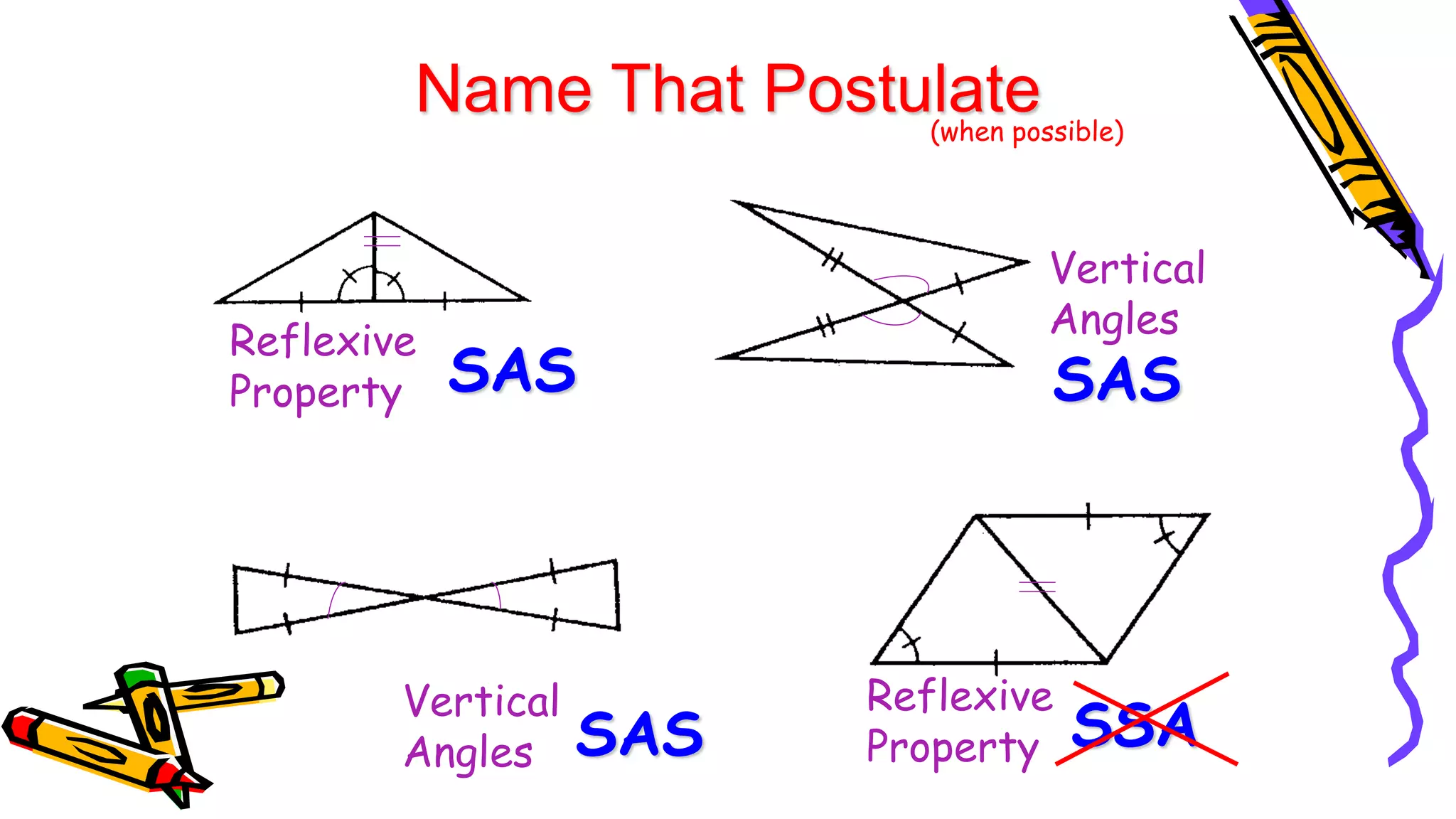
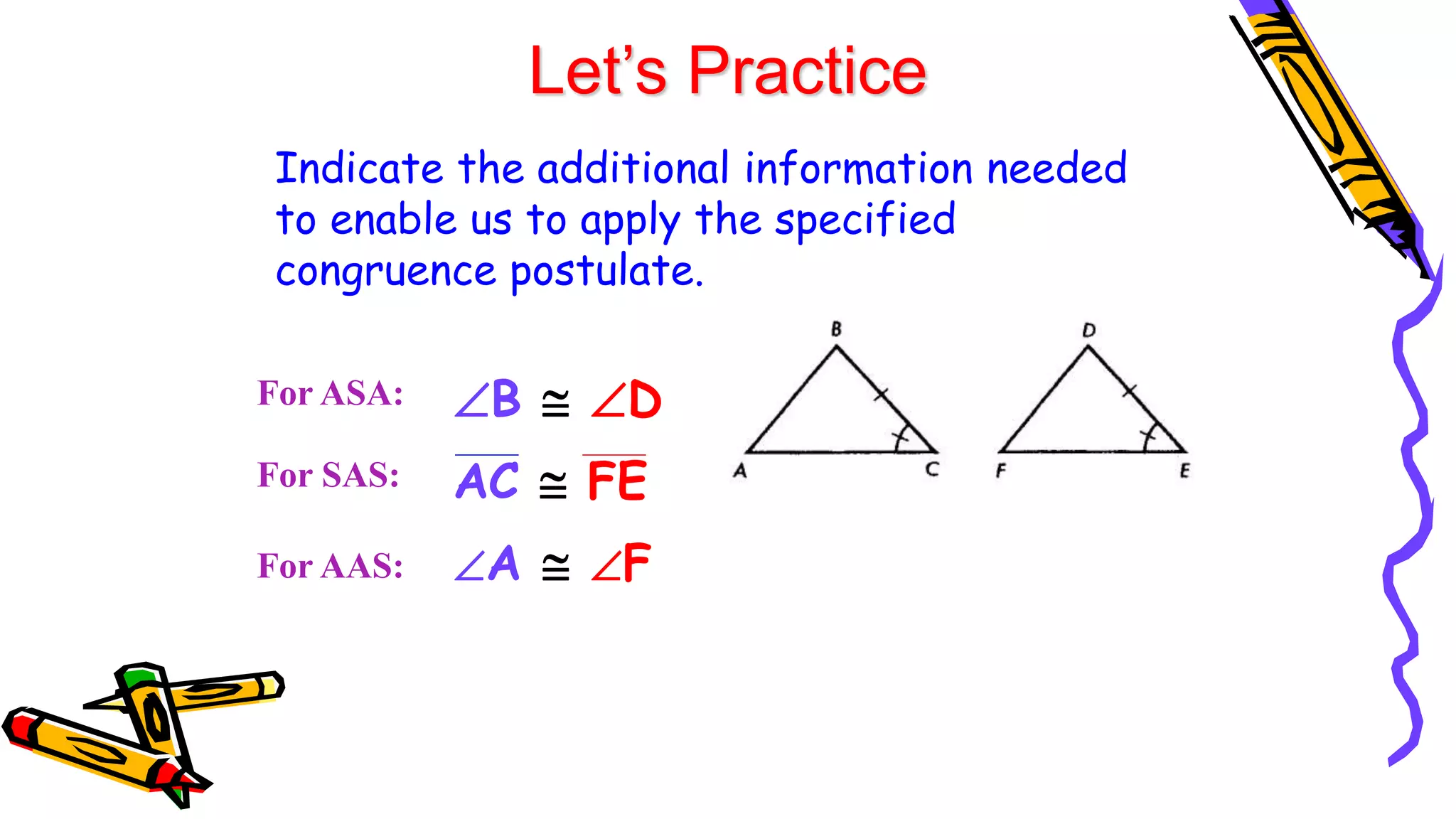
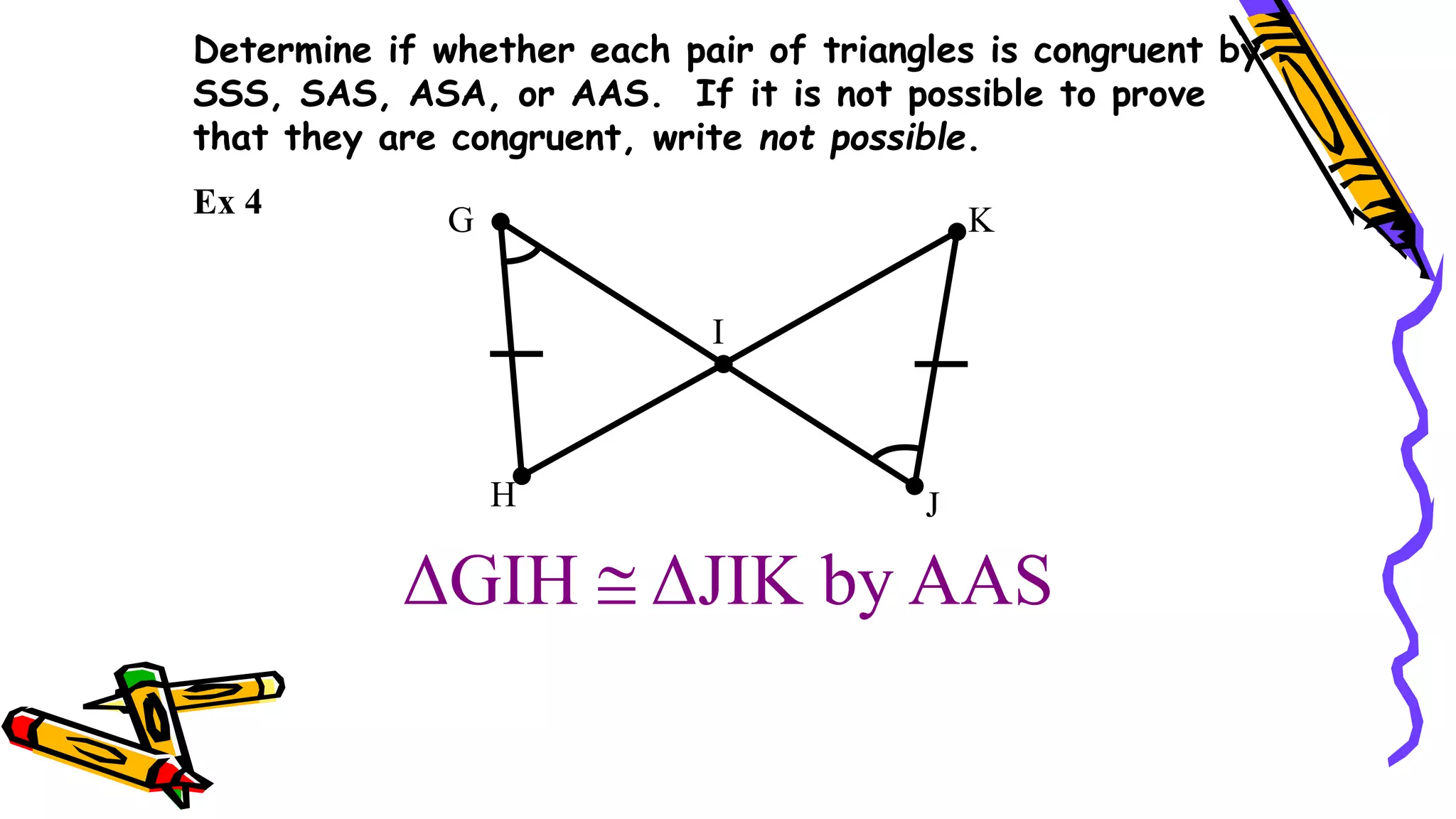
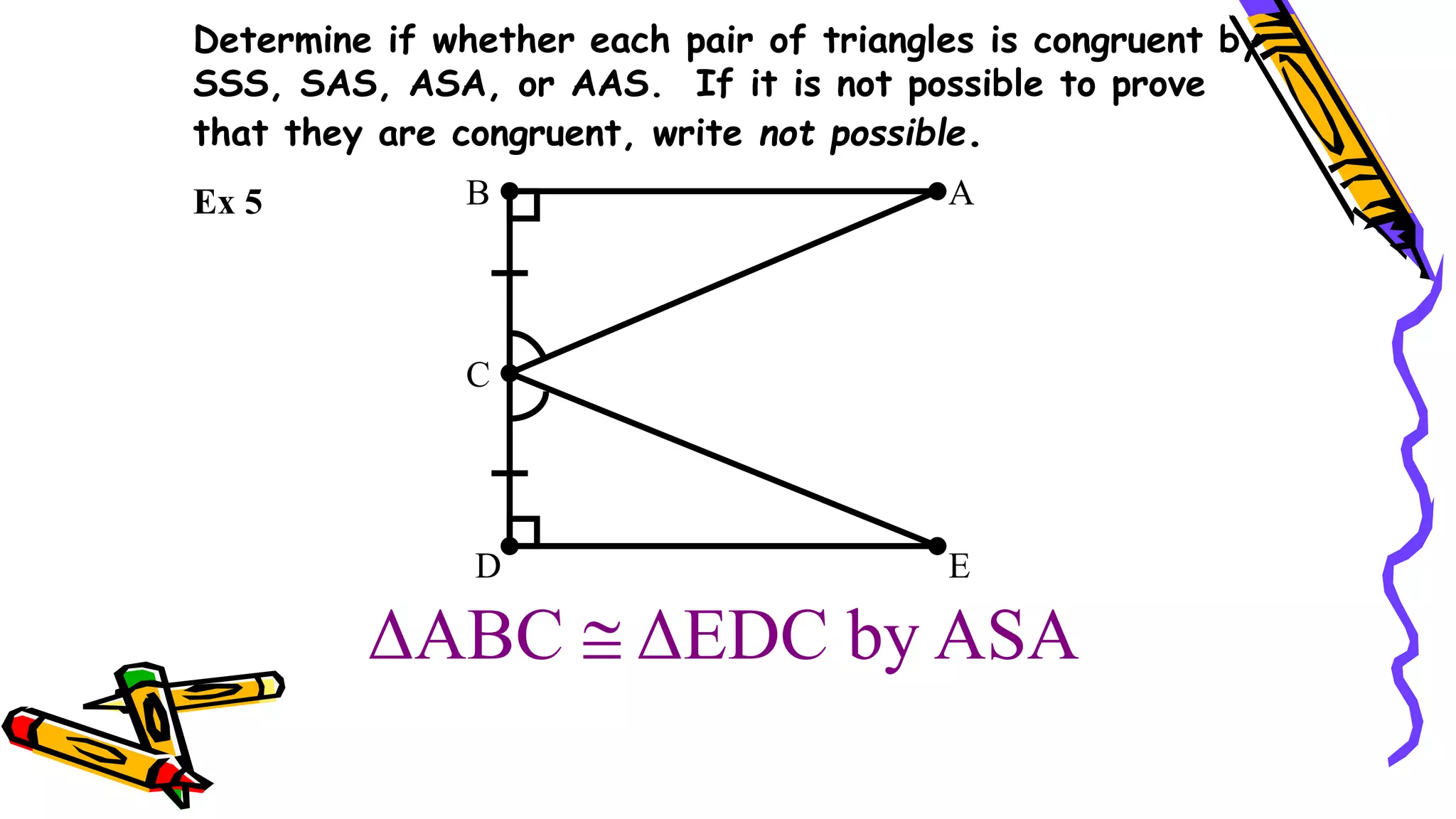
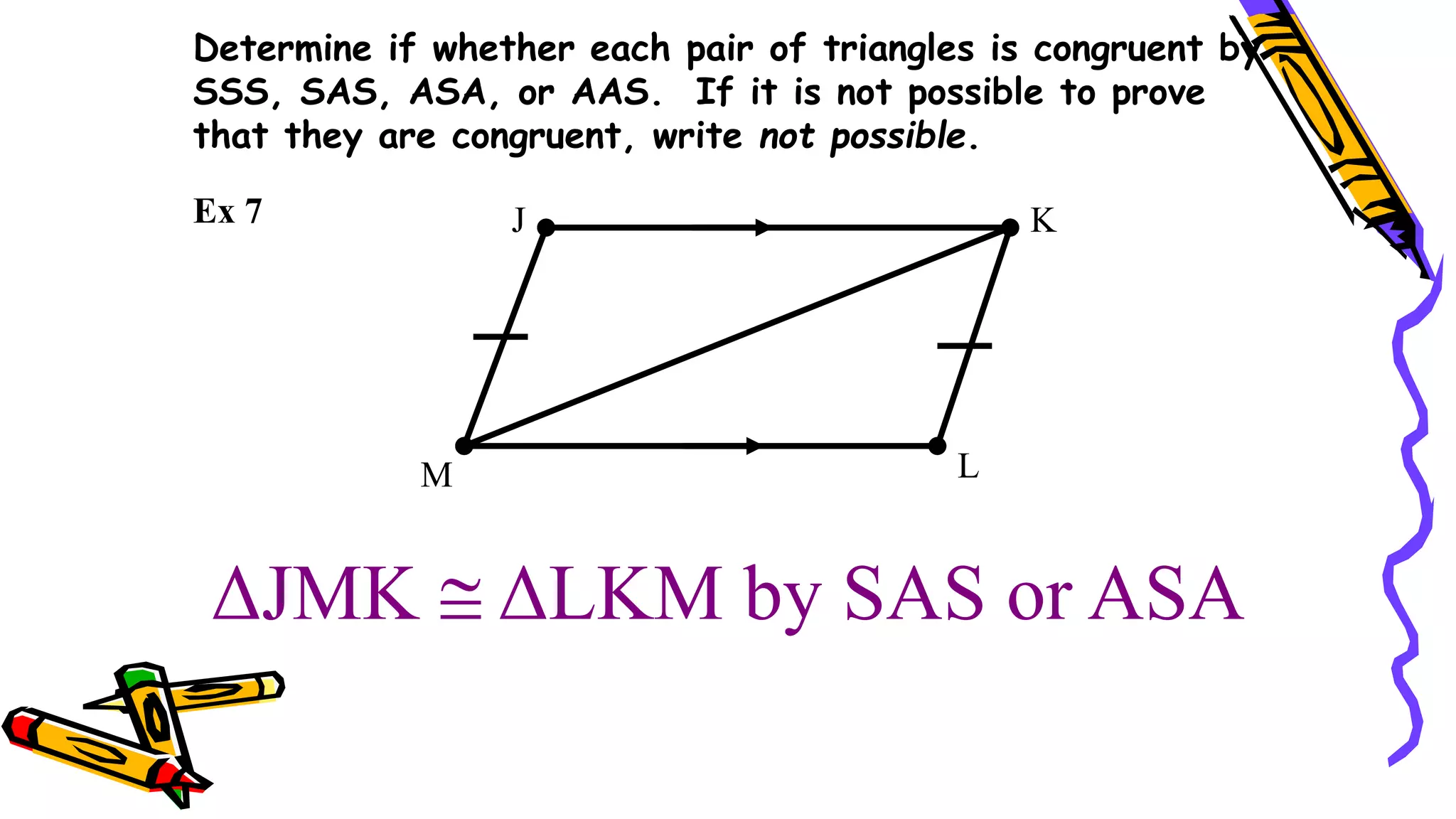
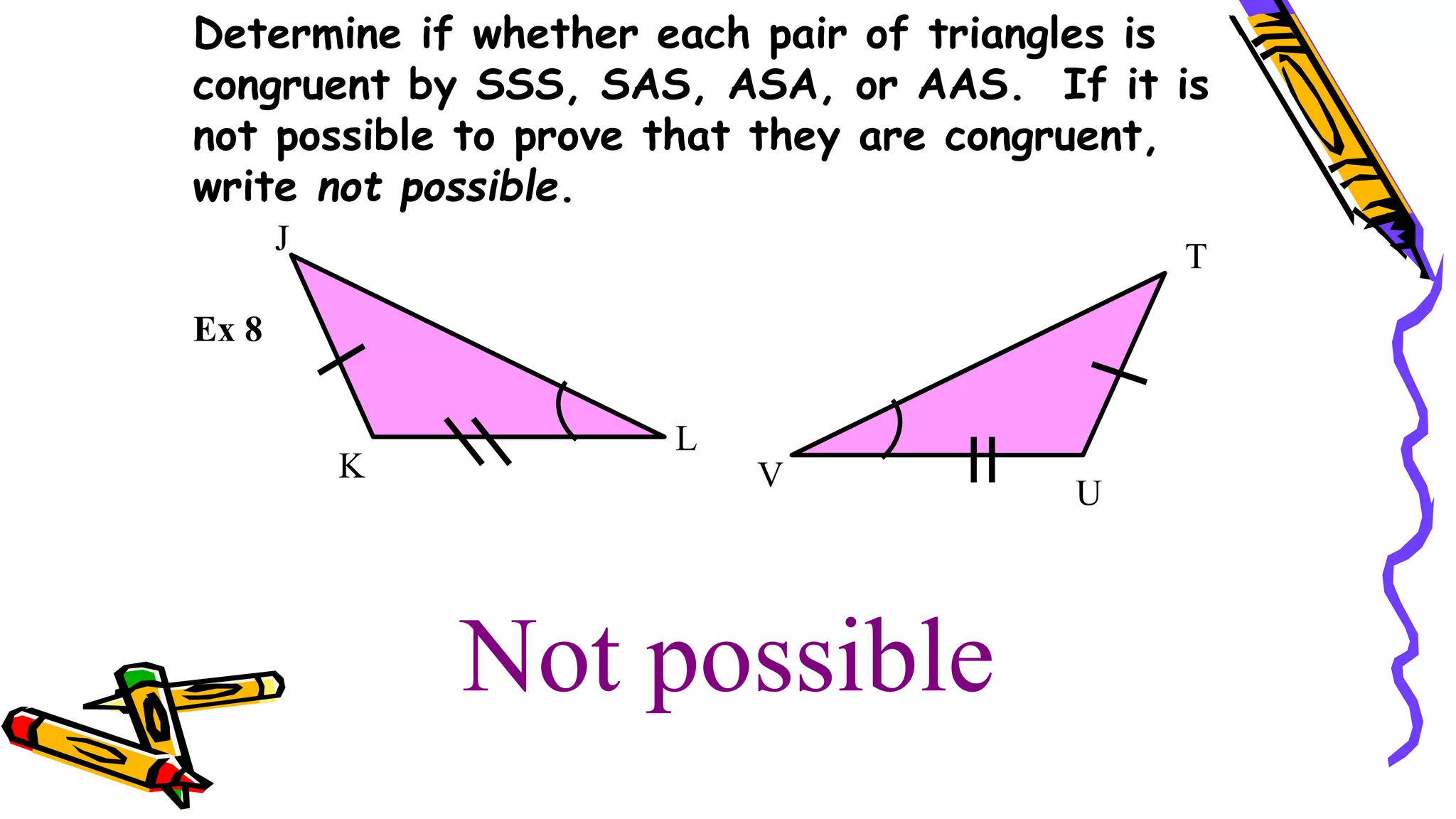
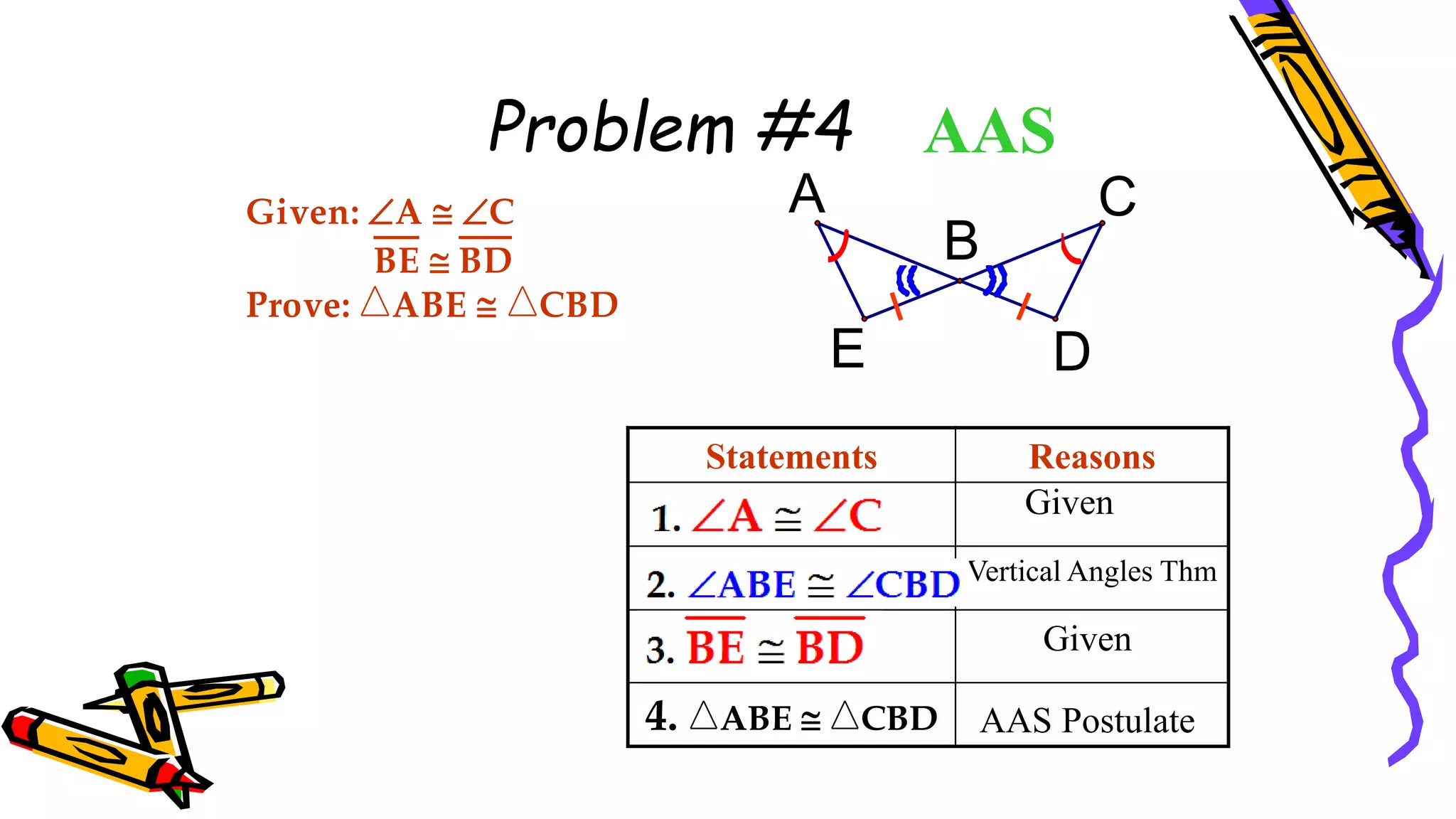
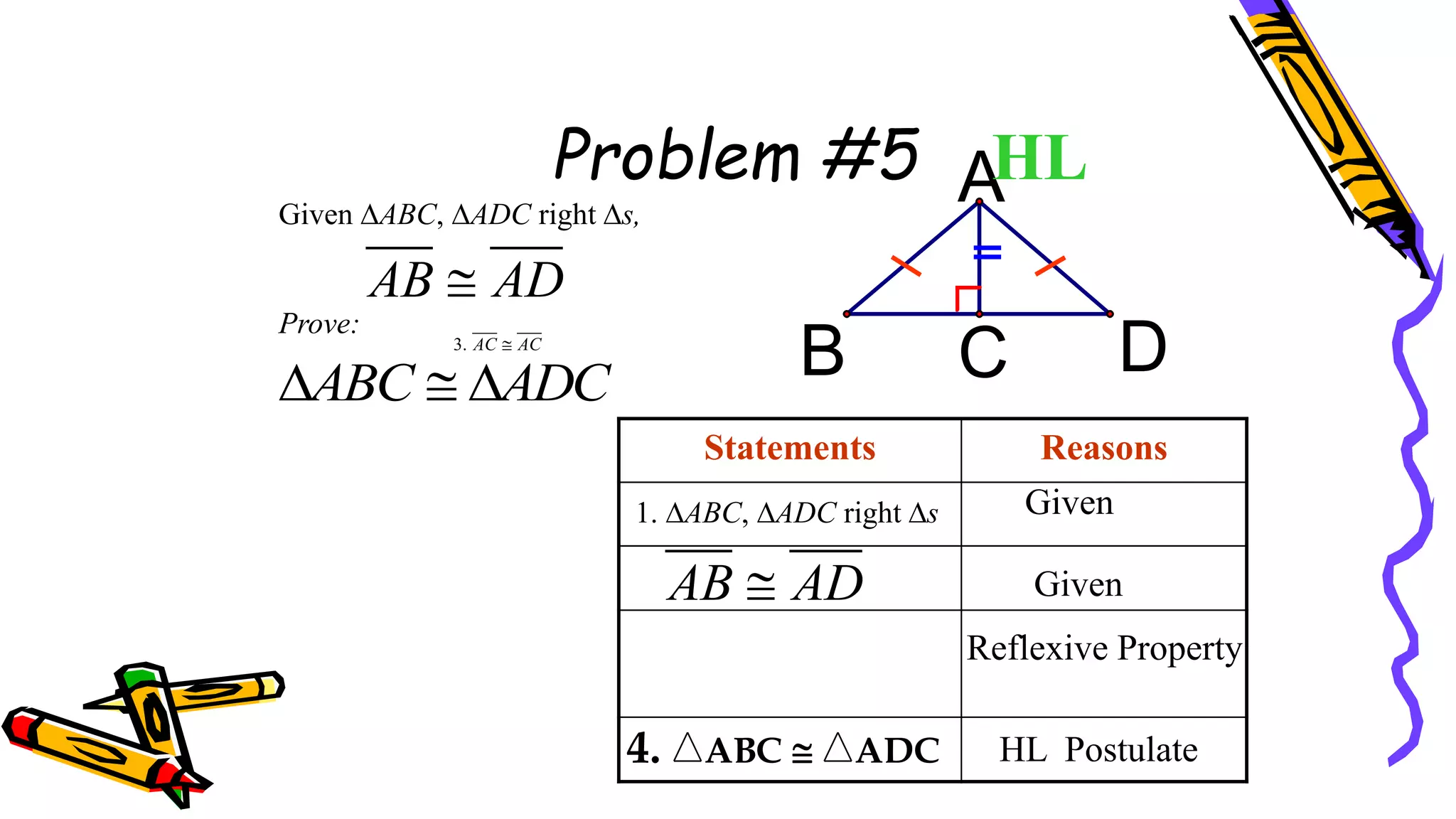
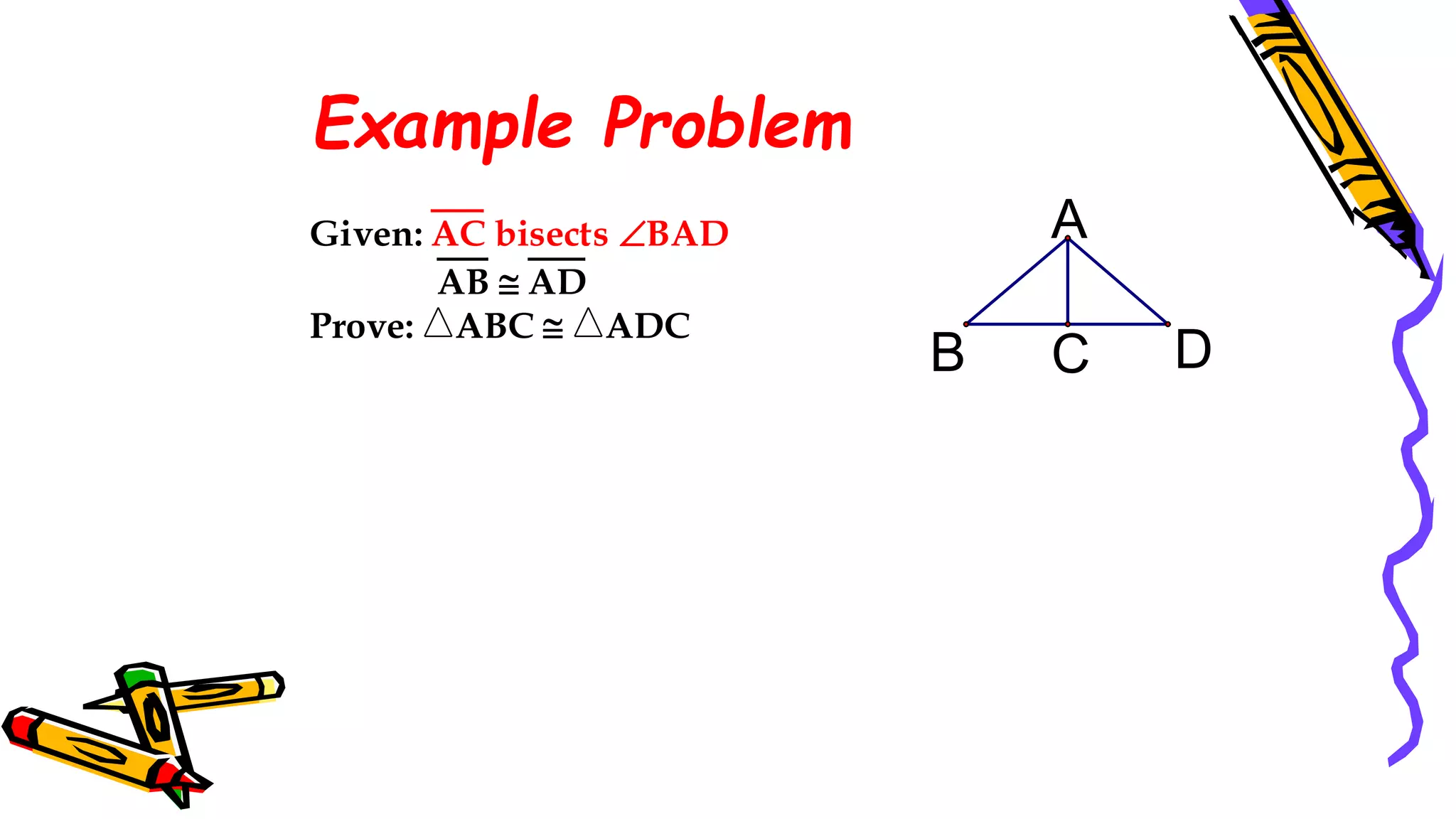
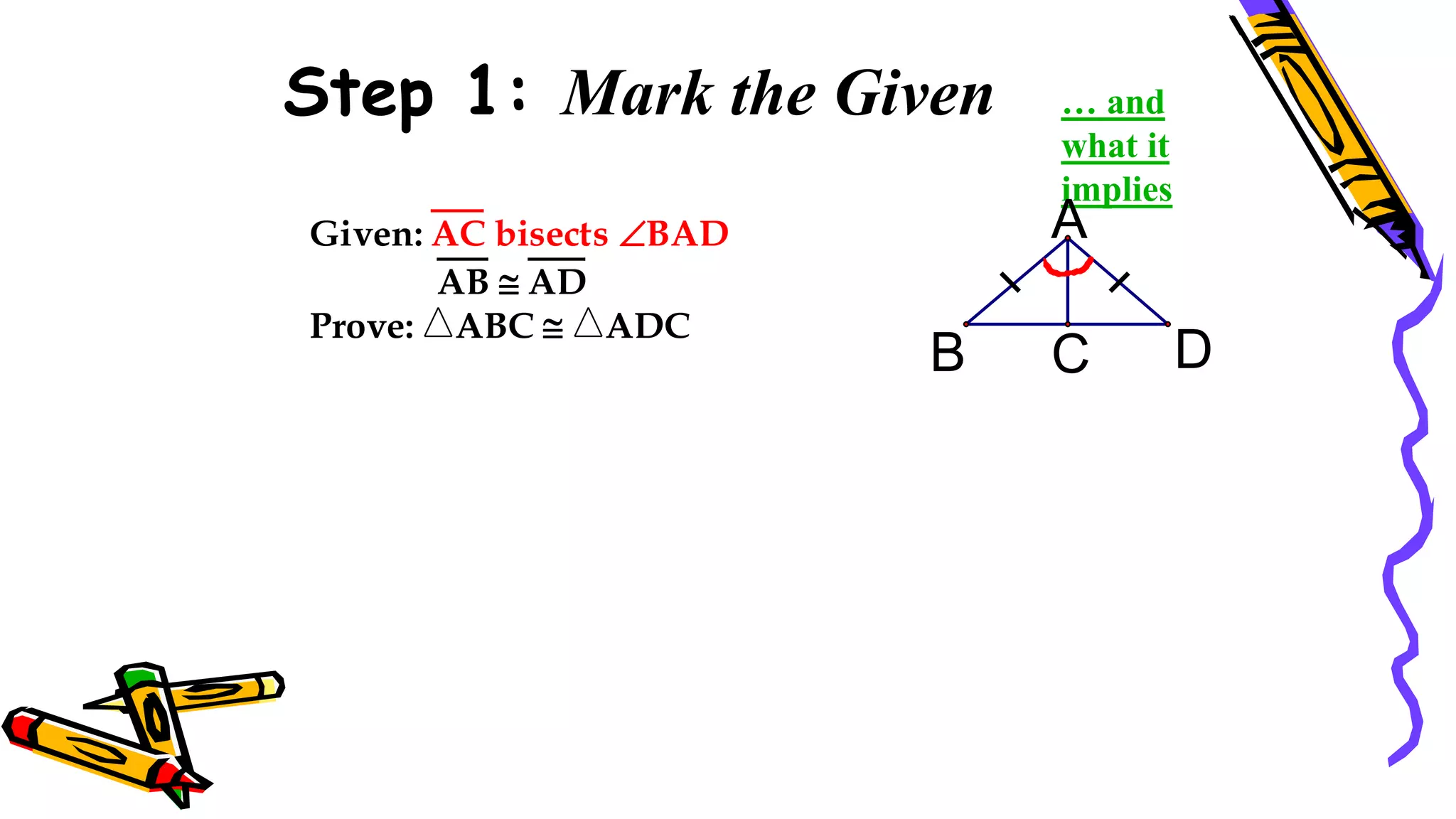
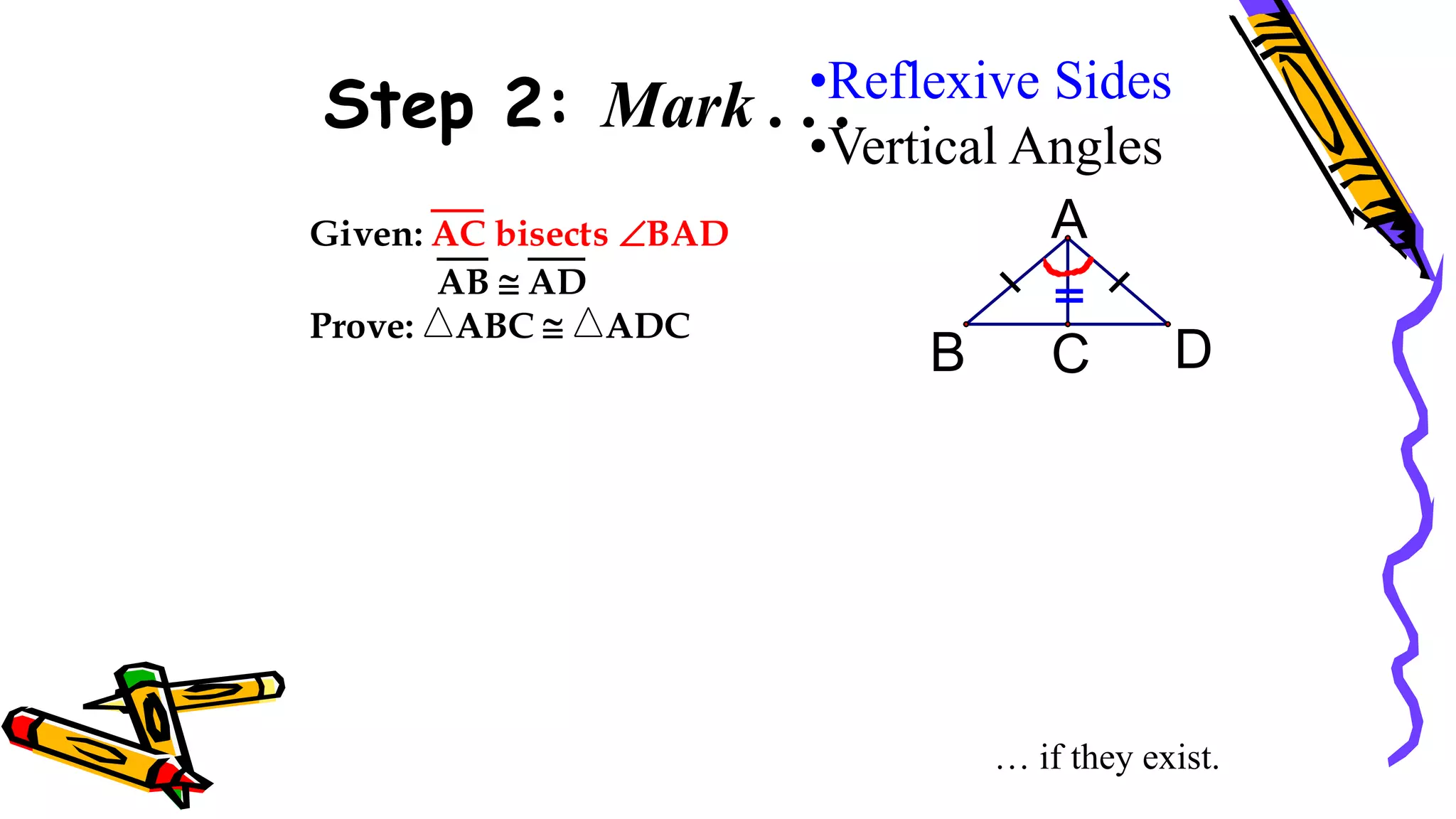
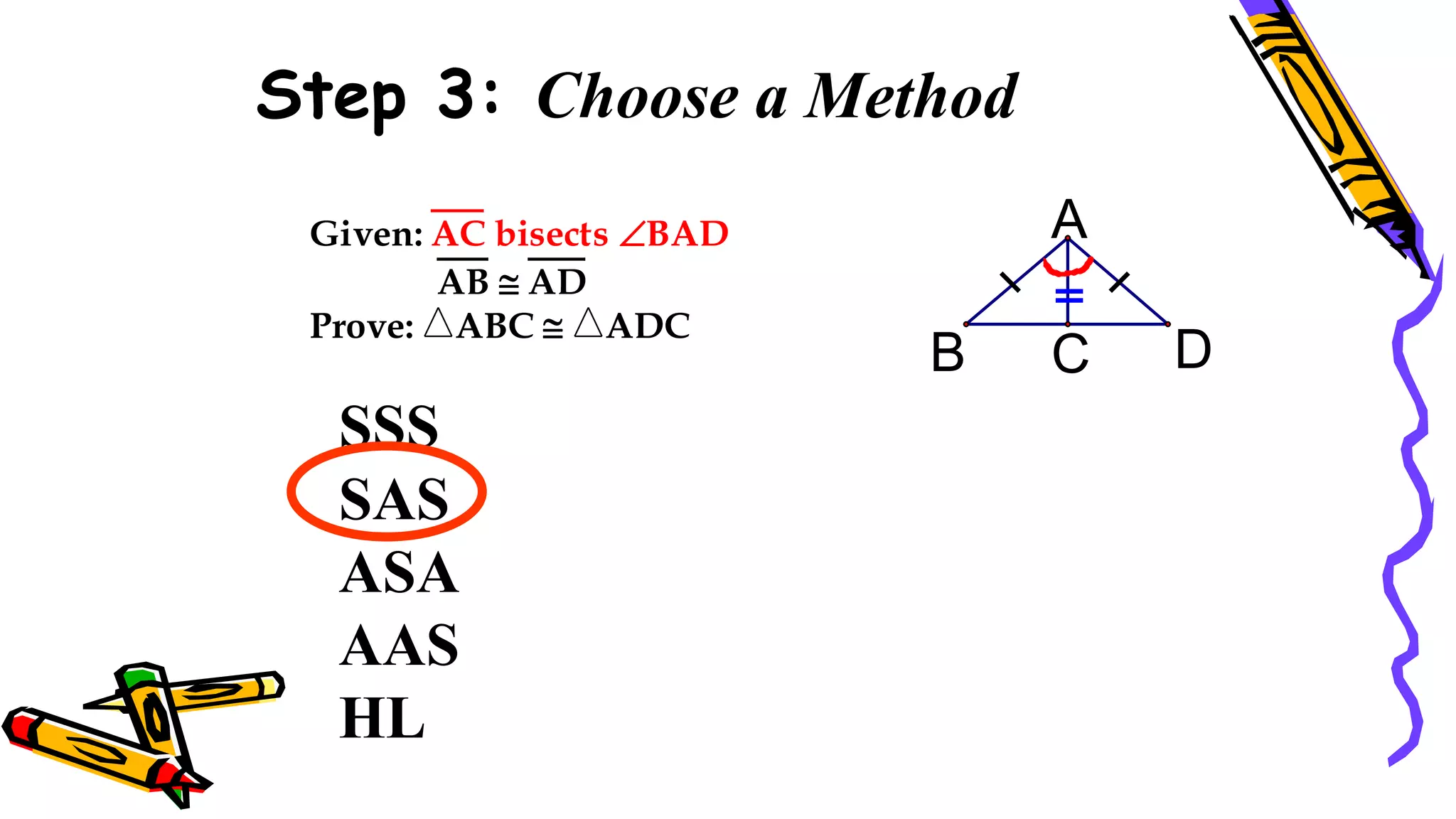
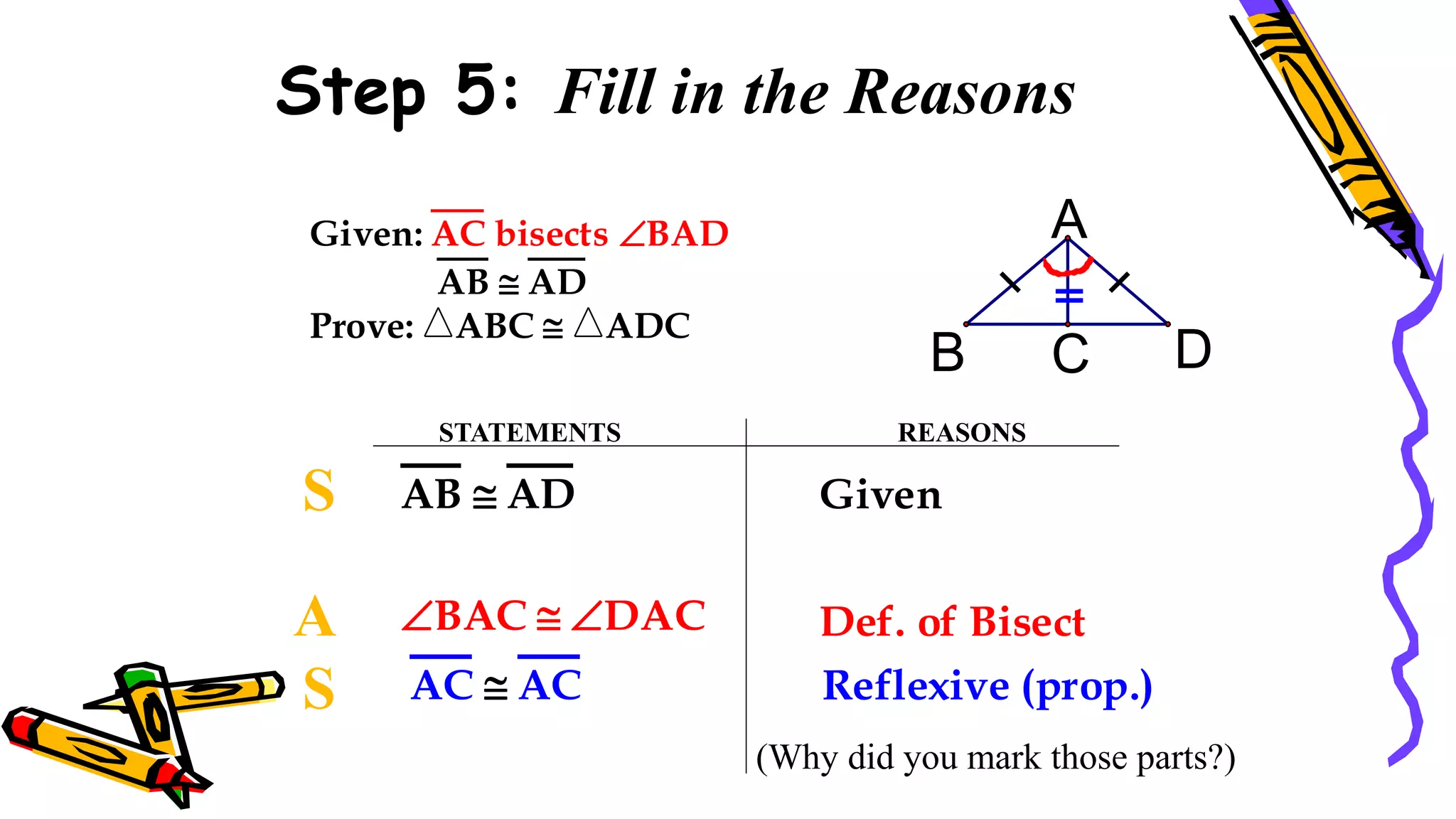
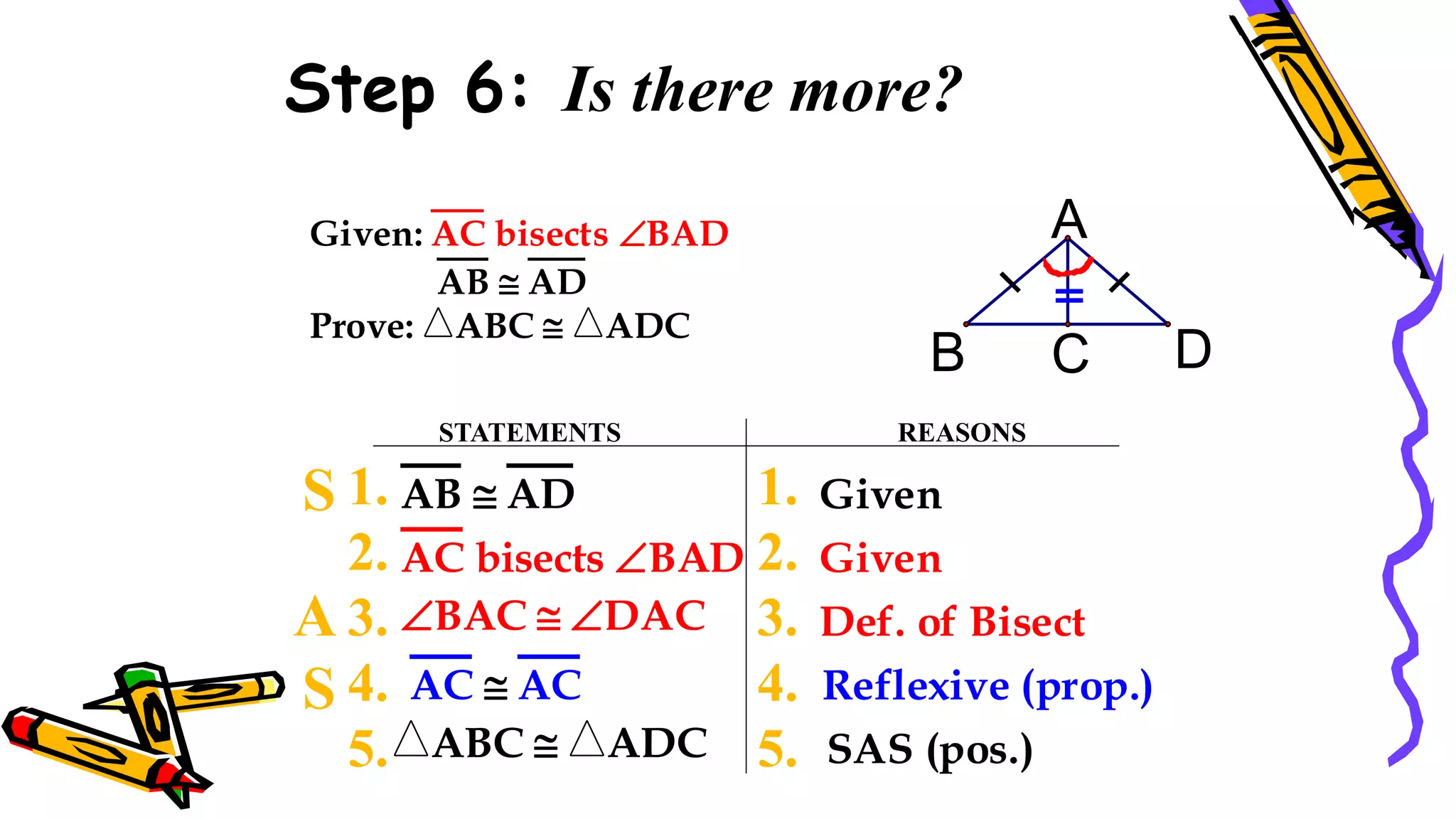
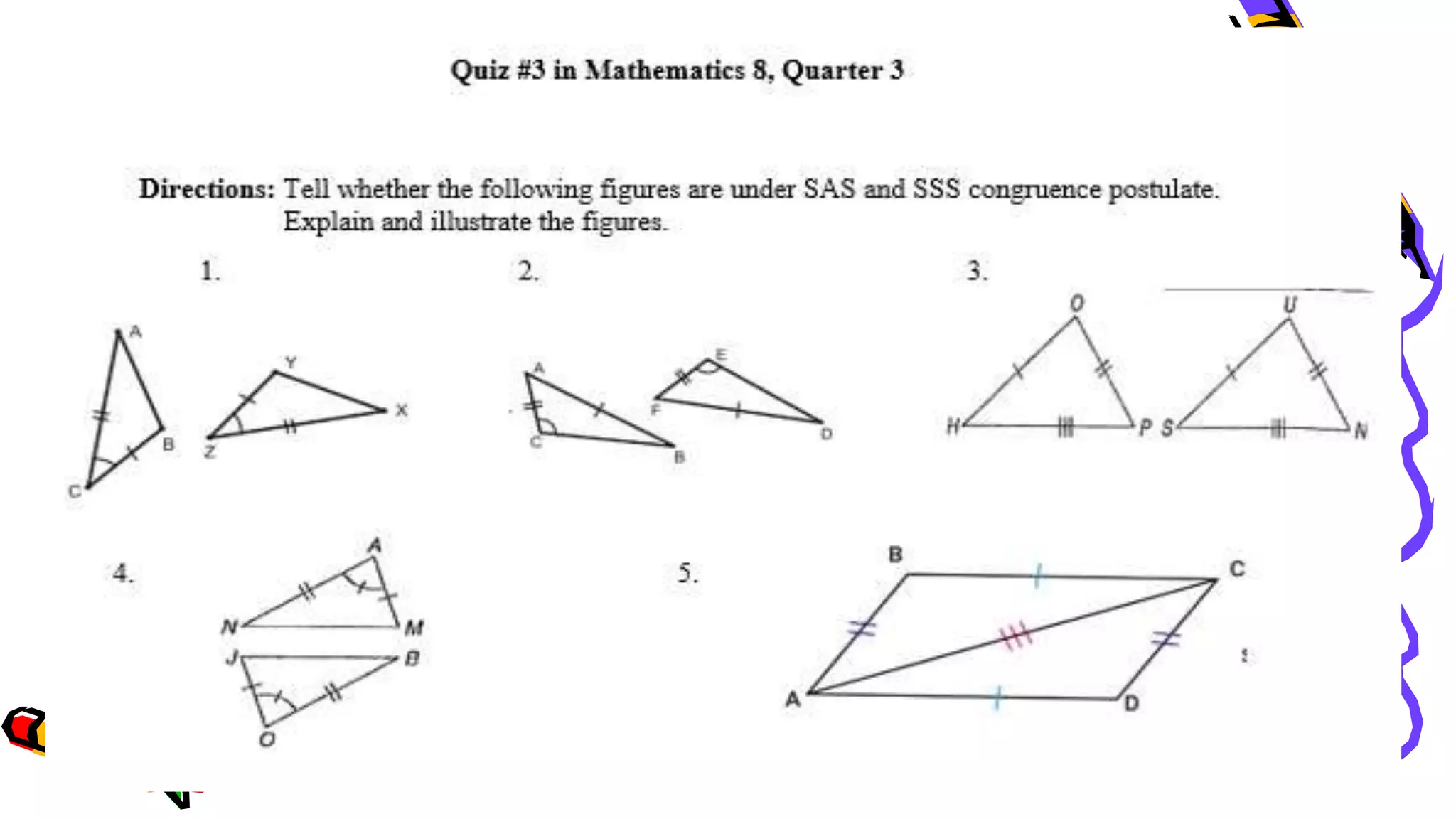
This document provides instructions and examples for illustrating triangle congruence. It begins with an activity asking students to identify whether figure pairs are congruent or not. Next, it discusses how to pair corresponding vertices, sides, and angles of congruent triangles. Examples are given demonstrating this process. The document then discusses different postulates for triangle congruence including SSS, SAS, and ASA. It provides additional examples and activities applying these postulates. It also discusses right triangle congruence and the corresponding theorems. In all, the document aims to teach students how to determine if two triangles are congruent and explain why using appropriate triangle congruence rules and terminology.

1. ILLUSTRATING
TRIANGLE
CONGRUENCE

2. ACTIVITY 1: Congruent or Not Congruent
Directions: Identify whether the two figures have the same size and
shape or not. Write YES if the figures have the same size and shape and
NO if not. Write your answer in a separate sheet of paper.
1.
2.
3.
4.
5.

3. 1. YES
2. NO
3. NO
4. YES
5. YES

4. Do you know that congruent figures can be seen in
real life?

6. It’s your turn! Match ∆ABC with ∆GHI. Fill- in the table and
give the corresponding vertices, sides, and angles of the
two triangles. Please refer to the previous example to get
the correct answer.
∆ABC ↔ ∆GHI
Corresponding
Vertices
Corresponding
Sides
Corresponding
Angles

7. Two triangles are congruent if their vertices can be
paired so that corresponding sides are congruent and
corresponding angles are congruent.

8. Illustrative Example 1:
ΔABC ≅ ΔDEF. This read as “triangle ABC is congruent to
triangle DEF.”
Note:
≅ symbol for congruency
∆ symbol for triangle

9. The congruent corresponding parts are marked
identically.
Process Questions:
1. How do you pair corresponding sides and angles?
2. How many pairs of corresponding parts are congruent if
two triangles are congruent?

10. Illustrative Example 2:
Given two identical triangles with marked congruent parts
so that ΔPRS ≅ ΔMLK, answer the questions below.
Process Questions:
1. What angle in ΔPRS is
congruent to ∠K in
ΔMLK?
2. What side of ΔKLM is
congruent to PS in
ΔSRP?

11. Directions: Given ΔABD ≅ ΔCBD, enumerate the six
pairs of the corresponding congruent parts. One
congruent part is done for you.
1.AB ≅ CB 4.
2. 5.
3. 6.

12. What is the importance of
illustrating triangle congruence
in real life situation?

13. How can you say that the two
triangles are congruent?
How do you pair corresponding
sides and angles?

14. 2. AX≅ ___ 5. ∠A ≅ ___
3. MX ≅ ___ 6. ∠X ≅ ___
1. MA ≅ ___ 4. ∠M ___
Activity 4: Complete the Missing Part!

15. Directions: Using KWL chart. Write what you learned
about triangle congruence. Complete the statement in
the box below. Write your answer in a separate sheet
of paper.

16. Thank You!

17. Illustrating SSS, SAS and ASA
Congruence Postulates

18. Activity 1: Give Me My Pair!
Directions: Identify the pairs of congruent sides and congruent angles of
the triangles below. Write your answer in a separate sheet of paper.

19. Congruent triangles are used to make the roofs of the
buildings and houses stable. We can also see congruent
triangles in the rails of the bridges to reinforce its
structure so that it will become strong and firm.
But how can we say that the two triangles are congruent?
We can use postulates on triangle congruence in order to
show that the two triangles are congruent. These
congruence postulates give ways on what pair of
corresponding parts illustrates triangle congruence.

21. Triangle Congruency Short-Cuts
If you can prove one of the following short
cuts, you have two congruent triangles
1. SSS (side-side-side)
2. SAS (side-angle-side)
3. ASA (angle-side-angle)
4. AAS (angle-angle-side)
5. HL (hypotenuse-leg) right triangles only!

22. Built – In Information in Triangles

23. Identify the ‘built-in’ part

24. Shared side
Parallel lines
-> AIA
Shared side
Vertical angles
SAS
SAS
SSS

25. SOME REASONS For Indirect
Information
• Def of midpoint
• Def of a bisector
• Vert angles are congruent
• Def of perpendicular bisector
• Reflexive property (shared side)
• Parallel lines ….. alt int angles
• Property of Perpendicular Lines

26. This is called a common side.
It is a side for both triangles.
We’ll use the reflexive property.

39. Triangle congruence may be applied using right
triangles. The parts of the triangle like legs, acute
angles and hypotenuse can be paired so that the
two right triangles are congruent. In this lesson,
you will be using the parts of the right triangles
to show that the two triangles are congruent
aside from SAS, ASA and SSS Congruence
Postulates

40. Picture puzzle

42. A triangle that has a right angle (90°).

44. Illustrating the Right
Triangle Congruence
Theorem

45. The right triangle congruence
theorem states that “ Two right
triangles are said to be congruent
if they are of the same shape and
size”.

46. Right triangle congruence can be proven in a number of
ways, ranging from a comparison of all three sides and
all three angles, or using one of the theorems (SSS,
SAS, AAS, or ASA) above. But, there are also four (4)
right triangle congruence theorems that can prove
congruence even more efficiently and quickly. These
four theorems are as follows:

47.  The leg-leg (LL) theorem.
 The leg-angle (LA) theorem.
 The hypotenuse-leg (HL) theorem.
 The hypotenuse-angle (HA) theorem.

48. Congruence
Theorem for Right
Triangles

52. HL( hypotenuse leg ) is used
only with right triangles, BUT,
not all right triangles.
HL ASA

54. Activity: What is My Statement?
Directions: Using the two congruent right triangles found in the Theme Park with markings
illustrated in the table below, give the two congruent parts and state what right triangle
congruence theorem used in the figure. The first one is done for you.

55. 20 15 10 5 0
Properly
illustrate
d the two
congruent
triangles.
Clearly
illustrate
d the two
congruent
triangles
Two
congruent
triangles
are
illustrate
d in
closely
manner
Two
congruent
triangles
are
illustrate
d in
unclear
manner
No output
presented

56. Guide Question (Reflection)
What other real-life applications of
the right triangle congruence can you
find in your surroundings? Justify
your answer.

57. What is right triangle
congruence theorem?
•What are the different theorems
on triangle congruence for right
triangles.

58. Quiz
Directions: State a congruence theorem. on right triangles. Write
your answers on separate sheet/s of paper.

59. Give three examples of right-
angled triangle that can be seen
in the surroundings

60. Name That Postulate
(when possible)
SAS
SAS
SAS
Reflexive
Property
Vertical
Angles
Vertical
Angles
Reflexive
Property SSA

61. Let’s Practice
Indicate the additional information needed
to enable us to apply the specified
congruence postulate.
For ASA:
For SAS:
B  D
For AAS: A  F
AC  FE

62. Determine if whether each pair of triangles is congruent by
SSS, SAS, ASA, or AAS. If it is not possible to prove
that they are congruent, write not possible.
ΔGIH  ΔJIK by AAS
G
I
H J
K
Ex 4

63. ΔABC  ΔEDC by ASA
B A
C
E
D
Ex 5
Determine if whether each pair of triangles is congruent by
SSS, SAS, ASA, or AAS. If it is not possible to prove
that they are congruent, write not possible.

64. ΔACB  ΔECD by SAS
B
A
C
E
D
Ex 6
Determine if whether each pair of triangles is congruent by
SSS, SAS, ASA, or AAS. If it is not possible to prove
that they are congruent, write not possible.

65. ΔJMK  ΔLKM by SAS or ASA
J K
L
M
Ex 7
Determine if whether each pair of triangles is congruent by
SSS, SAS, ASA, or AAS. If it is not possible to prove
that they are congruent, write not possible.

66. Not possible
K
J
L
T
U
Ex 8
Determine if whether each pair of triangles is
congruent by SSS, SAS, ASA, or AAS. If it is
not possible to prove that they are congruent,
write not possible.
V

67. Problem #4
Statements Reasons
AAS
Given
Given
Vertical Angles Thm
AAS Postulate
Given: A  C
BE  BD
Prove: ABE  CBD
E
C
D
A
B
4. ABE  CBD
88

68. Problem #5
3. AC AC

Statements Reasons
C
B D
AHL
Given
Given
Reflexive Property
HL Postulate
4. ABC  ADC
1. ABC, ADC right s
AB AD

Given ABC, ADC right s,
Prove:
AB AD

ABC ADC
  
89

69. Congruence Proofs
1. Mark the Given.
2. Mark …
Reflexive Sides or Angles / Vertical Angles
Also: mark info implied by given info.
3. Choose a Method. (SSS , SAS, ASA)
4. List the Parts …
in the order of the method.
5. Fill in the Reasons …
why you marked the parts.
6. Is there more?
90

70. Given implies Congruent
Parts
midpoint
parallel
segment bisector
angle bisector
perpendicular
segments

angles

segments

angles

angles

91

71. Example Problem
C
B D
A
Given: AC bisects BAD
AB  AD
Prove: ABC  ADC
92

72. Step 1: Mark the Given … and
what it
implies
C
B D
A
Given: AC bisects BAD
AB  AD
Prove: ABC  ADC
93

73. •Reflexive Sides
•Vertical Angles
Step 2: Mark . . .
… if they exist.
C
B D
A
Given: AC bisects BAD
AB  AD
Prove: ABC  ADC
94

74. Step 3: Choose a Method
SSS
SAS
ASA
AAS
HL
C
B D
A
Given: AC bisects BAD
AB  AD
Prove: ABC  ADC
95

75. Step 4: List the Parts
STATEMENTS REASONS
… in the order of the Method
C
B D
A
Given: AC bisects BAD
AB  AD
Prove: ABC  ADC
BAC  DAC
AB  AD
AC  AC
S
A
S
96

76. Step 5: Fill in the Reasons
(Why did you mark those parts?)
STATEMENTS REASONS
C
B D
A
Given: AC bisects BAD
AB  AD
Prove: ABC  ADC
BAC  DAC
AB  AD
AC  AC
Given
Def. of Bisector
Reflexive (prop.)
S
A
S
97

77. S
A
S
Step 6: Is there more?
STATEMENTS REASONS
C
B D
A
Given: AC bisects BAD
AB  AD
Prove: ABC  ADC
BAC  DAC
AB  AD
AC  AC
Given
AC bisects BAD Given
Def. of Bisector
Reflexive (prop.)
ABC  ADC SAS (pos.)
1.
2.
3.
4.
5.
1.
2.
3.
4.
5. 98

78. Congruent Triangles Proofs
1. Mark the Given and what it implies.
2. Mark … Reflexive Sides / Vertical Angles
3. Choose a Method. (SSS , SAS, ASA)
4. List the Parts …
in the order of the method.
5. Fill in the Reasons …
why you marked the parts.
6. Is there more?
104

79. Using CPCTC in Proofs
• According to the definition of congruence, if two
triangles are congruent, their corresponding parts
(sides and angles) are also congruent.
• This means that two sides or angles that are not
marked as congruent can be proven to be congruent
if they are part of two congruent triangles.
• This reasoning, when used to prove congruence, is
abbreviated CPCTC, which stands for
Corresponding Parts of Congruent Triangles are
Congruent.
105

80. Corresponding Parts of
Congruent Triangles
• For example, can you prove that sides AD and BC are
congruent in the figure at right?
• The sides will be congruent if triangle ADM is congruent
to triangle BCM.
– Angles A and B are congruent because they are marked.
– Sides MA and MB are congruent because they are marked.
– Angles 1 and 2 are congruent because they are vertical
angles.
– So triangle ADM is congruent to triangle BCM by ASA.
• This means sides AD and BC are congruent by CPCTC.
106

81. Corresponding Parts of
Congruent Triangles
• A two column proof that sides AD and BC
are congruent in the figure at right is shown
below:
Statement Reason
MA  MB Given
A  B Given
1  2 Vertical angles
ADM  BCM ASA
AD  BC CPCTC
107

82. Corresponding Parts of
Congruent Triangles
• A two column proof that sides AD and BC
are congruent in the figure at right is shown
below:
Statement Reason
MA  MB Given
A  B Given
1  2 Vertical angles
ADM  BCM ASA
AD  BC CPCTC
108

83. Corresponding Parts of
Congruent Triangles
• Sometimes it is necessary to add an auxiliary
line in order to complete a proof
• For example, to prove ÐR @ ÐO in this picture
Statement Reason
FR @ FO Given
RU @ OU Given
UF @ UF reflexive prop.
DFRU @ DFOU SSS
ÐR @ ÐO CPCTC
109

84. Corresponding Parts of
Congruent Triangles
• Sometimes it is necessary to add an auxiliary
line in order to complete a proof
• For example, to prove ÐR @ ÐO in this picture
Statement Reason
FR @ FO Given
RU @ OU Given
UF @ UF Same segment
DFRU @ DFOU SSS
ÐR @ ÐO CPCTC
110

85. Thank You!