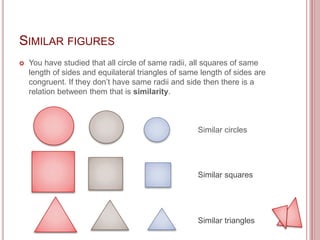
This document provides an introduction to triangles and similarity. It defines a triangle as a polygon with three line segments and notes that triangles are common shapes seen in daily life like road signs. It states that two polygons are similar if their corresponding angles are equal and the lengths of corresponding sides are proportional. Specifically for triangles, it provides the criteria that two triangles are similar if all corresponding angles are equal or if the corresponding sides are in the same ratio. The document also discusses theorems related to similarity such as AAA, SSS, and SAS similarity theorems.

1. TRI∆NGLES

2. INTRODUCTION TO TRIANGLES
 In our daily life, we come across numerous figure
which resemble a triangle. The most common
example would be of a road sign.
 This figure is known as a triangle. In simple words,
triangles is a polygon bounded by three line
segment (or sided).

3. SIMILAR FIGURES
 You have studied that all circle of same radii, all squares of same
length of sides and equilateral triangles of same length of sides are
congruent. If they don’t have same radii and side then there is a
relation between them that is similarity.
Similar circles
Similar squares
Similar triangles

4. WHAT IS SIMILARITY?
 Definition : Two polygons are said to be similar to
each other, if
i. Their corresponding angles are equal and
ii. The lengths of their corresponding side are
proportional.

5. SIMILAR TRIANGLES
Now we know about the similarity of polygons, we can easily deduce the case in
which two triangles will be similar.
Let us now consider two triangles, ∆ABC and ∆DEF
These two triangle will be similar if,
a) All the corresponding angle are equal
i.e. A = D, B = E, C = F
b) The corresponding side are in the same ratio
i.e. BC/EF = AC/DF = AB/DE
The above is also called the criteria of similarity of two triangles.
If one of the above conditions is met, then the two triangles ∆ABC and ∆DEF are
said to be similar i.e. ∆ABC  ∆DEF (‘  ’ denotes similarity).
Note:

6. Basic proportionality theorem (Thales’ theorem)
Statement: In a triangle, a line draw parallel to one side of a triangle intersecting the other two sides in distinct points,
divides the other two sides in the same ratio.

8. CRITERIA OF SIMILARITY

9. AAA SIMILARITY THEOREM
Proof:

11. SSS SIMILARITY THEOREM

13. SAS SIMILARITY THEOREM

14. THEOREM RELATED TO AREAS OF SIMILAR
TRIANGLES

16. PYTHAGORAS THEOREM

17. CONVERSE OF PYTHAGORAS THEOREM

18. QUICK RECAP

19. THANK YOU
&
DON’T FORGET TO
CLAP FOR US
Presented by Ayush