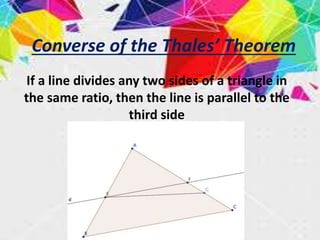
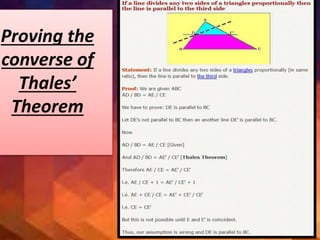
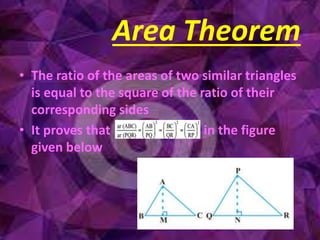
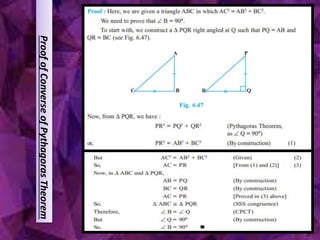
This document summarizes key concepts in geometry related to triangles. It discusses similarity criteria including AAA, SSA, and SSS. It also covers the area theorem, Pythagorean theorem, and its converse. The basic proportionality theorem and its converse are explained as well as how they relate to parallel lines. In summary, this document outlines important triangle properties and theorems for understanding similarity, area, right triangles, and parallel lines.

1. TrianglesTriangles
By GEETU
10-B

2. • Basic Proportionality Theorem
• Similarity Criteria
• Area Theorem
• Pythagoras Theorem
What will you learn?

3. A triangle is a polygon with three edges and
three vertices. It is one of the
basic shapes in geometry.

4. BASIC
PROPORTIONALITY
THEOREM
• Basic
Proportionality
Theorem states that
if a line is drawn
parallel to one side
of a triangle to
intersect the other
2 points , the other
2 sides are divided
in the same ratio.
• It was discovered
by Thales , so also
known as Thales
theorem.

5. Proving
The Thales’
Theorem

6. Converse of the Thales’ Theorem
If a line divides any two sides of a triangle in
the same ratio, then the line is parallel to the
third side

7. Proving the
converse of
Thales’
Theorem

8. Similarity Criteria
Similarity Criteria's
SSS ASA AA

9. • If in two triangles, corresponding angles are
equal, then their corresponding sides are in
the same ratio (or proportion) and hence the
two triangles are similar.
• In Δ ABC and Δ DEF if ∠ A=∠ D, ∠ B= ∠E and ∠
C =∠ F then Δ ABC ~ Δ DEF.
AAA Similarity

10. • If in two triangles, sides of one triangle are
proportional to (i.e., in the same ratio of ) the
sides of the other triangle, then their
corresponding angles are equal and hence
the two triangles are similar.
• In Δ ABC and Δ DEF if AB/DE =BC/EF =CA/FD
then Δ ABC ~ Δ DEF.
SSS Similarity

11. • If one angle of a triangle is equal to one angle
of the other triangle and the sides including
these angles are proportional, then the two
triangles are similar.
• In Δ ABC and Δ DEF if AB/DE =BC/EF and ∠
B= ∠E then Δ ABC ~ Δ DEF.
SAS Similarity

12. • The ratio of the areas of two similar triangles
is equal to the square of the ratio of their
corresponding sides
• It proves that in the figure
given below
Area Theorem

13. Proof
Of
Area
Theorem

14. • If a perpendicular is drawn from the vertex of the right angle of a
right triangle to the hypotenuse then triangles on both sides of the
perpendicular are similar to the whole triangle and to each other
• In a right triangle, the square of the hypotenuse is equal to the sum
of the squares of the other two sides.
• In a right triangle if a and b are the lengths of the legs and c is the
length of hypotenuse, then a² + b² = c².
• It states Hypotenuse² = Base² + Altitude².
• A scientist named Pythagoras discovered the theorem, hence came
to be known as Pythagoras Theorem.
Pythagoras Theorem

15. Pythagoras Theorem

16. ProofofPythagorasTheorem

17. In a triangle, if square of one side is equal to the
sum of the squares of the other two sides, then
the angle opposite the first side is a right angle.
Converse of Pythagoras Theorem

18. ProofofConverseofPythagorasTheorem

19. • Two figures having the same shape but not necessarily
the same size are called similar figures.
• All the congruent figures are similar but the converse is
not true.
• Two polygons of the same number of sides are similar, if
(i) their corresponding angles are equal and (ii) their
corresponding sides are in the same ratio (i.e.,
proportion).
• If a line is drawn parallel to one side of a triangle to
intersect the other two sides in distinct points, then the
other two sides are divided in the same ratio.
• If a line divides any two sides of a triangle in the same
ratio, then the line is parallel to the third side.
Summary

20. • If in two triangles, corresponding angles are equal, then their corresponding sides
are in the same ratio and hence the two triangles are similar (AAA similarity
criterion).
• If in two triangles, two angles of one triangle are respectively equal to If in two
triangles, corresponding angles are equal, then their corresponding sides are in
the same ratio and hence the two triangles are similar (AAA similarity criterion).
• If in two triangles, two angles of one triangle are respectively equal to the two
angles of the other triangle, then the two triangles are similar (AA similarity
criterion).
• If in two triangles, corresponding sides are in the same ratio, then their
corresponding angles are equal and hence the triangles are similar (SSS similarity
criterion).
• If one angle of a triangle is equal to one angle of another triangle and the sides
including these angles are in the same ratio (proportional), then the triangles are
similar (SAS similarity criterion).
• The ratio of the areas of two similar triangles is equal to the square of the ratio of
their corresponding sides.
Summary

21. • If a perpendicular is drawn from the vertex of the right angle of a right
triangle to the hypotenuse, then the triangles on both sides of the
perpendicular are similar to the whole triangle and also to each other.
• In a right triangle, the square of the hypotenuse is equal to the sum of
the squares of the other two sides (Pythagoras Theorem).
• If in a triangle, square of one side is equal to the sum of the squares of
the other two sides, then the angle opposite the first side is a right angle.
Summary

22. THANK YOU FOR
HAVING A
GRACEFUL EYE ON
MY EFFORTED PPT.
SUBMITTED
TO :
MS. GEETA