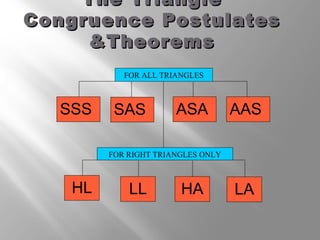
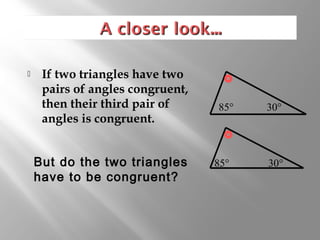
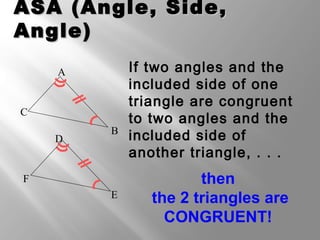
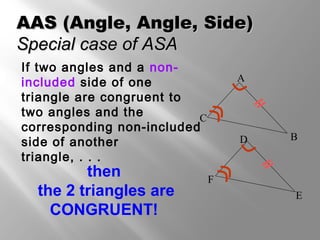
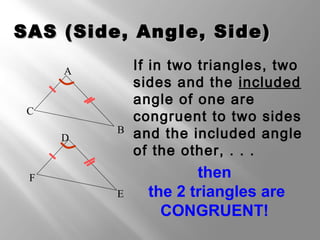
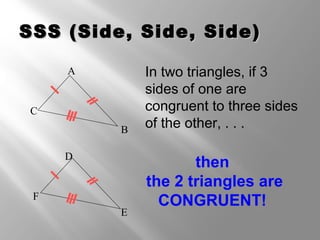
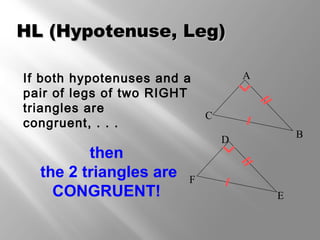
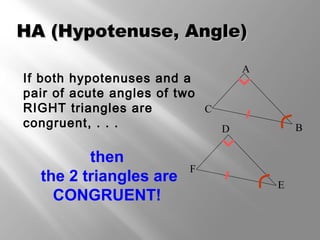
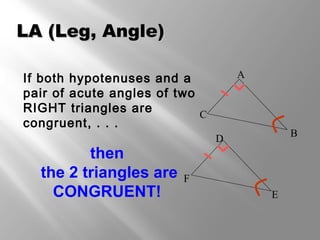
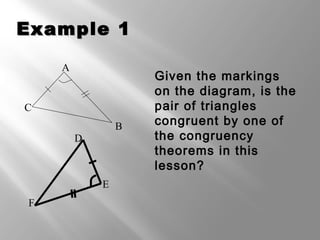
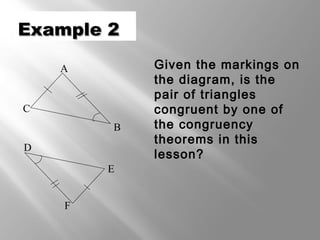
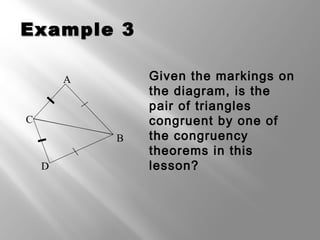
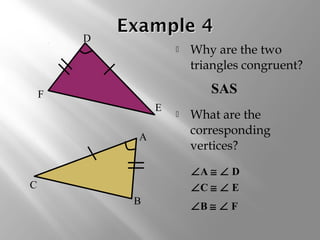
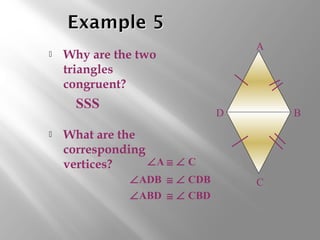
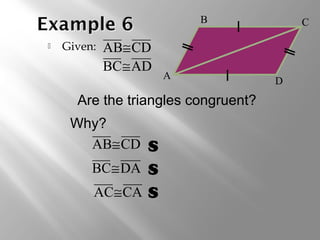
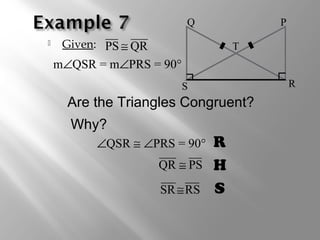
This document discusses triangle congruence theorems. It explains that triangles can be proven congruent in different ways beyond just having three pairs of congruent sides and angles. The main triangle congruence theorems covered are: SAS, SSS, ASA, AAS, HL, HA, LL, and LA. It provides examples applying these theorems to determine if pairs of triangles are congruent. The document also addresses right triangles and the additional theorems used to prove those congruent: HL, HA, LL, and LA.

1. TTrriiaannggllee CCoonnggrruueennccee TThheeoorreemmss

2.  Congruent triangles have three congruent
sides and and three congruent angles.
 However, triangles can be proved
congruent without showing 3 pairs of
congruent sides and angles.

3. TThhee TTrriiaannggllee
CCoonnggrruueennccee PPoossttuullaatteess
&&TThheeoorreemmss
FOR ALL TRIANGLES
SSS SAS ASA AAS
FOR RIGHT TRIANGLES ONLY
HL LL HA LA

4.  If two angles in one triangle are
congruent to two angles in another
triangle, the third angles must also be
congruent.
Think about it… they have to
add up to 180°.

5.  If two triangles have two
pairs of angles congruent,
then their third pair of
angles is congruent.
But do the two triangles
have to be congruent?
85° 30°
85° 30°

6. 30°
30°
Why aren’t these triangles congruent?
What do we call these triangles?

7.  So, how do we prove
that two triangles really
are congruent?

8. AASSAA ((AAnnggllee,, SSiiddee,,
AAnnggllee))
If two angles and the
included side of one
triangle are congruent
to two angles and the
included side of
another triangle, . . .
then
the 2 triangles are
CONGRUENT!
F
E
A
D
C
B

9. AAAASS ((AAnnggllee,, AAnnggllee,, SSiiddee))
SSppeecciiaall ccaassee ooff AASSAA
If two angles and a non-included
side of one
triangle are congruent to
two angles and the
corresponding non-included
side of another
triangle, . . .
then
the 2 triangles are
CONGRUENT!
F
E
A
D
C
B

10. SAS ((SSiiddee,, AAnnggllee,, SSiiddee))
If in two triangles, two
sides and the included
angle of one are
congruent to two sides
and the included angle
of the other, . . .
then
the 2 triangles are
CONGRUENT!
F
E
A
D
C
B

11. SSS ((SSiiddee,, SSiiddee,, SSiiddee))
In two triangles, if 3
sides of one are
congruent to three sides
of the other, . . .
F
E
A
D
C
B
then
the 2 triangles are
CONGRUENT!

12. HHLL ((HHyyppootteennuussee,, LLeegg))
A
If both hypotenuses and a
pair of legs of two RIGHT
triangles are
congruent, . . .
C
B
F
E
D
then
the 2 triangles are
CONGRUENT!

13. HHAA ((HHyyppootteennuussee,, AAnnggllee))
If both hypotenuses and a
pair of acute angles of two
RIGHT triangles are
congruent, . . .
then
the 2 triangles are
CONGRUENT!
F
E
D
A
C
B

14. LLAA ((LLeegg,, AAnnggllee))
If both hypotenuses and a
pair of acute angles of two
RIGHT triangles are
congruent, . . .
then
the 2 triangles are
CONGRUENT!
A
C
B
F
E
D

15. LLLL ((LLeegg,, LLeegg))
If both pair of legs of two
RIGHT triangles are
congruent, . . .
then
the 2 triangles are
CONGRUENT!
A
C
B
F
E
D

16. EExxaammppllee 11
Given the markings
on the diagram, is the
pair of triangles
congruent by one of
the congruency
theorems in this
lesson?
F
E
D
A
C
B

17. EExxaammppllee 22
Given the markings on
the diagram, is the
pair of triangles
congruent by one of
the congruency
theorems in this
lesson?
A
C
B
F
E
D

18. EExxaammppllee 33
Given the markings on
the diagram, is the
pair of triangles
congruent by one of
the congruency
theorems in this
A
D lesson?
C
B

19.  Why are the two
triangles congruent?
F SAS
 What are the
corresponding
vertices?
A
B
C
D
E
ÐA @ Ð D
ÐC @ Ð E
ÐB @ Ð F

20.  Why are the two
triangles
congruent?
 What are the
corresponding
vertices?
A
B
C
D
SSS
ÐA @ Ð C
ÐADB @ Ð CDB
ÐABD @ Ð CBD

21.  Given:
B C
A D
AB@CD
BC@AD
Are the triangles congruent?
AB@CD
BC@DA
AC@CA
S
S
S
Why?

22.  Given: PS @ QR
Q
S R
Are the Triangles Congruent?
R
H
ÐQSR @ ÐPRS = 90°
SR@RS S
P
T
mÐQSR = mÐPRS = 90°
QR @ PS
Why?

23. ASA - Pairs of congruent sides contained
between two congruent angles
AAS – Pairs of congruent angles and
the side not contained between them.
SAS - Pairs of congruent angles
contained between two congruent sides
SSS - Three pairs of congruent sides

24. HL – Pair of sides including the
Hypotenuse and one Leg
HA – Pair of hypotenuses and one acute
angle
LL – Both pair of legs
LA – One pair of legs and one pair of
acute angles

25. All rights belong to their respective
owners.
Copyright Disclaimer Under
Section 107 of the Copyright Act
1976, allowance is made for fair
use for purposes such as criticism,
comment, news reporting,
TEACHING, scholarship, and
research.
Fair use is a use permitted by
copyright statute that might
otherwise be infringing.
Non-profit, EDUCATIONAL or
personal use tips the balance in
favor of fair use.