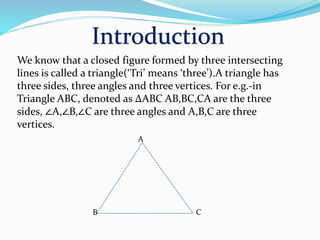
This document defines triangle congruence and the different criteria used to determine if two triangles are congruent. Two triangles are congruent if their corresponding sides and angles are equal. The criteria include: SAS (two sides and the included angle), ASA (two angles and the included side), AAS (any two angles and a non-included side), SSS (all three sides), and RHS (right angle, hypotenuse, and one other side). Examples are provided to demonstrate each congruence rule.

2. Introduction
We know that a closed figure formed by three intersecting
lines is called a triangle(‘Tri’ means ‘three’).A triangle has
three sides, three angles and three vertices. For e.g.-in
Triangle ABC, denoted as ∆ABC AB,BC,CA are the three
sides, ∠A,∠B,∠C are three angles and A,B,C are three
vertices.
A
B C

3. OBJECTIVES IN THIS LESSON
DEFINE THE CONGRUENCE OF
TRIANGLE.
STATE THE CRITERIA FOR THE
CONGRUENCE OF TWO TRIANGLES

4. DEFINING THE CONGRUENCE OF TRIANGLE:-
Let us take ∆ABC and ∆XYZ such that
corresponding angles are equal and
corresponding sides are equal :-
A
B C
X
Y Z
CORRESPONDING PARTS
∠A=∠X
∠B=∠Y
∠C=∠Z
AB=XY
BC=YZ
AC=XZ

5. Now we see that sides of ∆ABC coincides with sides of
∆XYZ.
A
B C
X
Y Z
SO WE GET THAT
TWO TRIANGLES ARE CONGRUENT, IF ALL THE SIDES AND
ALL THE ANGLES OF ONE TRIANGLE ARE EQUAL TO THE
CORRESPONDING SIDES AND ANGLES OF THE OTHER
TRIANGLE.
Here, ∆ABC ≅ ∆XYZ

6. This also means that:-
A corresponds to X
B corresponds to Y
C corresponds to Z
For any two congruent triangles the corresponding
parts are equal and are termed as:-
CPCT – Corresponding Parts of Congruent Triangles

7. Two triangles are congruent if two sides and the included
angle of one triangle are equal to the two sides and the
included angle of other triangle.
SAS
Two triangles are congruent if two angles and the included
side of one triangle are equal to two angles and the
included side of other triangle.
ASA
Two triangles are congruent if any two pairs of angle and
one pair of corresponding sides are equal.
AAS
If three sides of one triangle are equal to the three sides of
another triangle, then the two triangles are congruent.
SSS
If in two right-angled triangles the hypotenuse and one
side of one triangle are equal to the hypotenuse and one
side of the other triangle, then the two triangles are
congruent.
RHS

8. A
B C
P
Q R
S(1) AC = PQ
A(2) ∠C = ∠R
S(3) BC = QR
Now If,
Then ∆ABC ≅ ∆PQR (by SAS congruence)

9. A
B C
D
E F
Now If, A(1) ∠BAC = ∠EDF
S(2) AC = DF
A(3) ∠ACB = ∠DFE
Then ∆ABC ≅ ∆DEF (by ASA congruence)

10. A
B C P
Q
R
Now If, A(1) ∠BAC = ∠QPR
A(2) ∠CBA = ∠RQP
S(3) BC = QR
Then ∆ABC ≅ ∆PQR (by AAS congruence)

11. Now If, S(1) AB = PQ
S(2) BC = QR
S(3) CA = RP
A
B C
P
Q R
Then ∆ABC ≅ ∆PQR (by SSS congruence)

12. Now If, R(1) ∠ABC = ∠DEF = 90°
H(2) AC = DF
S(3) BC = EF
A
B C
D
E F
Then ∆ABC ≅ ∆DEF (by RHS congruence)

13. RECAPTULATION QUESTIONS
1. Define triangle?
2. What is congruence of triangle?
3. What is SAS triangle?
4. What is Hypotenous triangle?
5. What is SAS triangle?

14. FOLLOWUP ACTIVITY:
1) What are the triangles observed in real life situation?
2)List out the examples for congruence of triangles.

15. REFERENCES
 CLASS IX NCERT MATHEMATICS TEXT BOOK.
 WWW.BYJUS.COM

16. THANK YOU