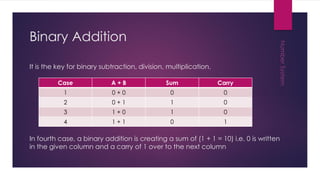
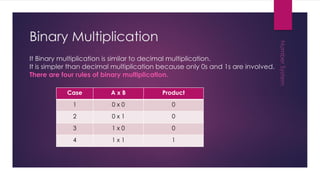
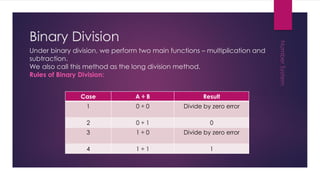
This document discusses different number systems including non-positional, positional, decimal, binary, octal, and hexadecimal systems. It provides examples of converting between these systems, such as converting the octal number 3450 to decimal. Binary arithmetic operations including addition, subtraction, multiplication, and division are also covered. The key steps and rules for performing each binary operation are outlined.

1. Number System
Presented By: Roshan Maharjan

2. Types Of Number System
➢
➢

3. Non- Positional Number System
➢
➢
➢

4. Positional Number System
➢
➢
•
•
•
➢

5. Decimal Number System
➢
➢
➢
➢
➢
➢
➢

6. Binary Number System
➢
➢
➢
➢
➢
➢
➢

7. Octal Number System
➢
➢
➢
➢
➢
➢
➢

8. Hexadecimal Number System
➢
➢
➢
➢
➢
➢
➢

9. Converting a number of Another Base
to Decimal Number System
➢

10. Converting a number of Another Base
to Decimal Number System
Example :
(3450)8 = ?10
(3450)8 = 3 x 8^3 + 4 x 8^2 + 5 x 8^1 + 0 x 8^0
= 3 x 512 + 4 x 64 + 5 x 8 + 0 x 1
= 1536 + 256 + 40 +0
= (1832)10
Common
values
multiplied by
the
corresponding
digits

11. Converting a Decimal Number
System to a number of Another Base
➢

12. Converting a Decimal Number System
to a number of Another Base

13. Converting a Decimal Number System
to a number of Another Base
0 1
2
2
2
2
2
2
43
21
10
5
2
1
1
1
0
1
0

14. Converting a Decimal Number System
to Octal Number System
8 43
8 5
0
3
5

15. Converting a Decimal Number System
to Hexadecimal Number System
16
16
423
26
1
7
A (10)
16
0 1

16. Converting Binary Number System to
Decimal Number System

17. Converting Octal Number System to
Decimal Number System

18. Converting Hexadecimal Number
System to Decimal Number System

19. Binary Arithmetic
•
•
•
•

20. Binary Addition
It is the key for binary subtraction, division, multiplication.
In fourth case, a binary addition is creating a sum of (1 + 1 = 10) i.e. 0 is written
in the given column and a carry of 1 over to the next column
Case A + B Sum Carry
1 0 + 0 0 0
2 0 + 1 1 0
3 1 + 0 1 0
4 1 + 1 0 1

21. Binary Addition

22. Binary Subtraction
Subtraction and Borrow, these two words will be used very frequently for the
binary subtraction.
There are four rules of binary subtraction.
In fourth case, we see that 0 – 1 creates an ambiguity. We consider this as a
borrow case and borrow 1 from the immediate left bit. Thus, this becomes 10
(decimal 2). Thus, 2-1 gives 1.
Case A - B Subtract Borrow
1 0 – 0 0 0
2 1 – 0 1 0
3 1 – 1 0 0
4 0 – 1 0 1

23. Binary Subtraction

24. Binary Multiplication
It Binary multiplication is similar to decimal multiplication.
It is simpler than decimal multiplication because only 0s and 1s are involved.
There are four rules of binary multiplication.
Case A x B Product
1 0 x 0 0
2 0 x 1 0
3 1 x 0 0
4 1 x 1 1

25. Binary Multiplication

26. Binary Division
Under binary division, we perform two main functions – multiplication and
subtraction.
We also call this method as the long division method.
Rules of Binary Division:
Case A ÷ B Result
1 0 ÷ 0 Divide by zero error
2 0 ÷ 1 0
3 1 ÷ 0 Divide by zero error
4 1 ÷ 1 1

27. Rules For Binary Division

28. Binary Division
Quotient = 111
Remainder = 0

29. Thank You