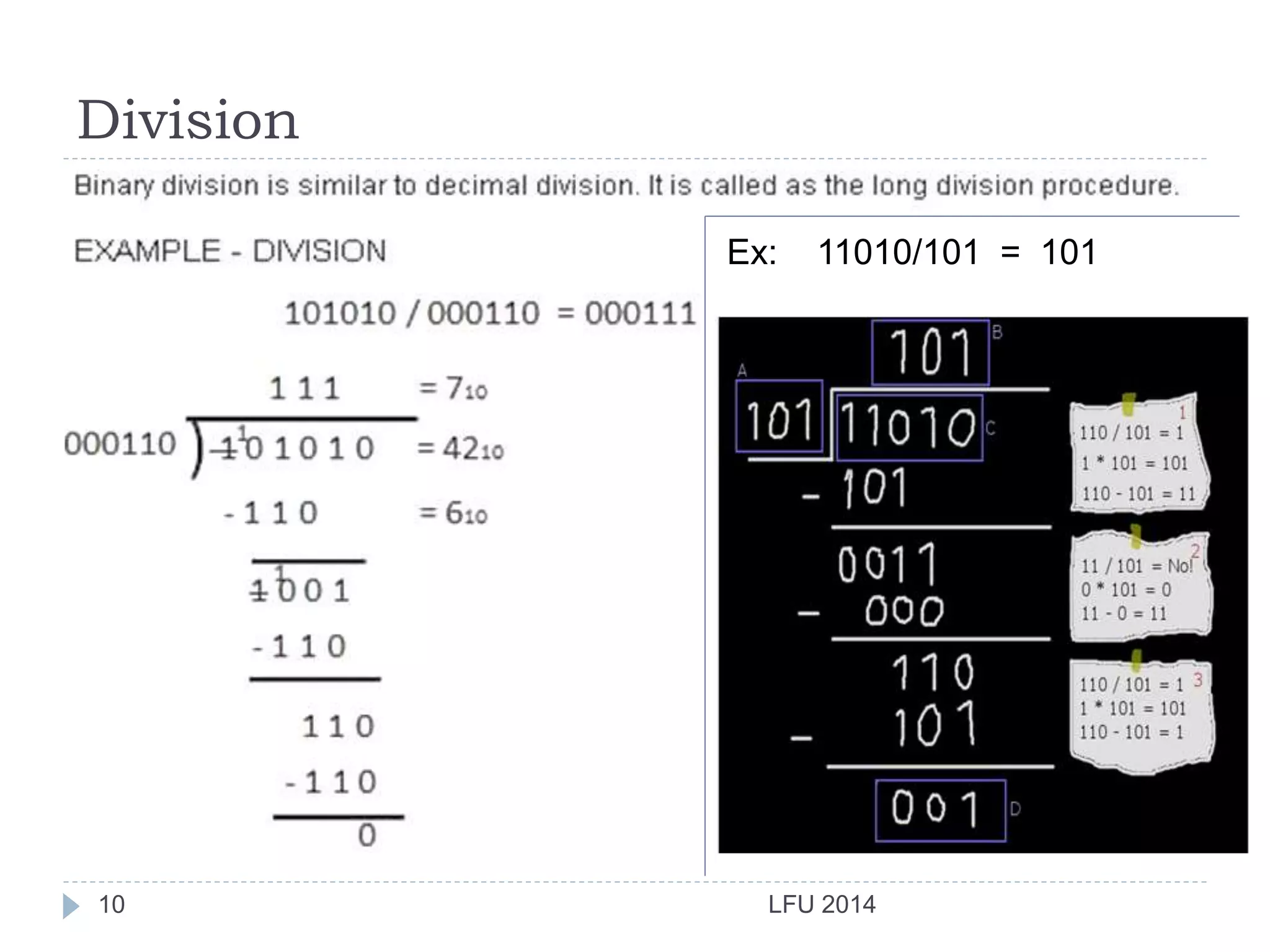
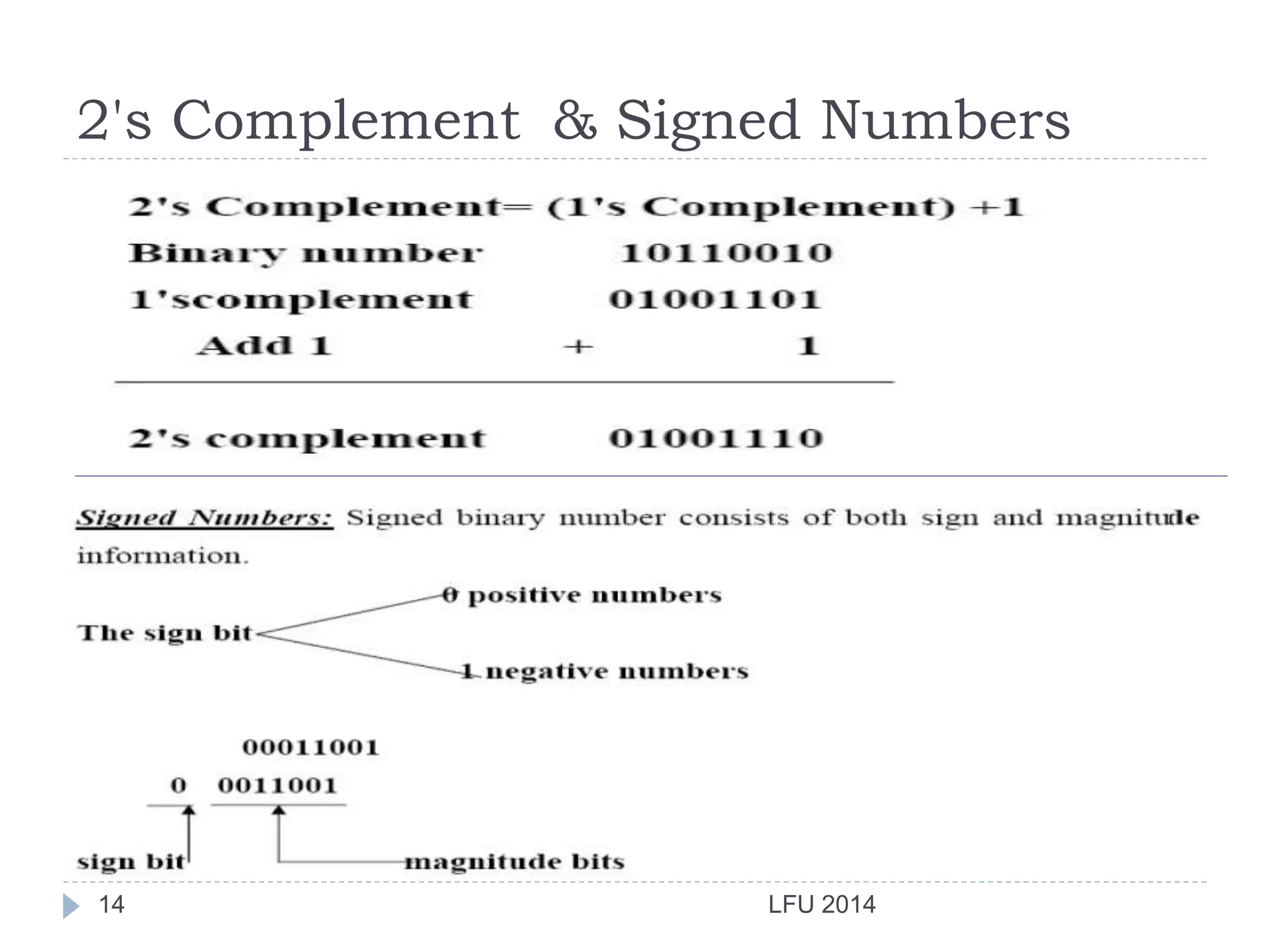
The document discusses various binary number systems including binary addition, subtraction, multiplication and division, 1's and 2's complement representation of signed numbers, binary coded decimal, Gray code for error correction in digital communications, and excess-3 code which is a complementary BCD code where the equivalent decimal is converted by adding 3. Examples are provided to illustrate binary arithmetic operations and conversions between number systems.

1. Prepared By
Asst. Lect. Mohammed Salim
Department of IT
1 LFU 2014

2. Contents
LFU 20142
Binary Addition, Subtraction, Multiplication,
Division
1's Complement of Binary Number.
2's Complement of Binary Number.
Signed Numbers & Binary Coded Decimal (BCD)
Gray Code
Excess-3 Code

3. Notes
LFU 20143

4. What is Binary Arithmetic?
LFU 20144
 Binary arithmetic is essential part of all the digital
computers and many other digital system such as
mobile phones .
 Binary numbers are NUMBERS: That means you
can add, subtract, multiply, and divide.
 2 + 2 = 4 , and
in Binary: 10 + 10 = 100

5. Binary Addition Rules
Rules:
 0 + 0 = 0
 0 + 1 = 1
 1 + 0 = 1
 1 + 1 = 10= 0 with 1 to carry
 1 + 1 + 1 =11 = 1 with 1 to carry
11_
11 0011
+ 1011
11 1110
carried bits

6. Addition Example & Practice
LFU 20146
 Ex: 1110 + 1010 = 11000
 Ex: 1001 + 111= 10000
 Ex: 1111 0000 + 1111 = 1111 1111
 Now take a few minutes to try these two:
 111 1000 + 1111
 1000 1100 + 1100 0110

7. Subtraction
LFU 20147
 The rules for binary subtraction are:
Binary
1002
- 0012
-------
0112
0-1 = 1; with borrow of 1
from next column
0 -1 (borrow) - 0 = 1, with
borrow of 1
1 - 1 (borrow) - 0 = 0.
Answer = 0112.

8. Subtraction Example & Practice
LFU 20148
Now take a few minutes to try these two:
100001 – 11111= ?
11100 - 1111 = ?

9. Multiplication
LFU 20149

10. Division
LFU 201410
Ex: 11010/101 = 101

11. LFU 201411
1's Complement of Binary Number
 As the binary system has base radix = 2. So the two types of
complements for the binary system are 2's complement and 1's
complement.
 Complements are used in the digital computers in order to simplify
the subtraction operation and for the logical manipulations, and also
to represent negative numbers.
 The 1's complement of a number is found by changing all 1's to 0's
and all 0's to 1's. This is called as taking complement or 1's
complement. Example of 1's Complement is:
Note: All complements should deal with a specific byte or bit size. For example the number above
is 5bits long.

12. LFU 201412
1's Complement Problems

13. 2's Complement of Binary Number
LFU 201413
 The 2's complement of binary number is obtained by adding 1 to the
Least Significant Bit (LSB) of 1's complement of the number.
 2's complement = 1's complement + 1
 Example of 2's Complement is as follows.
The problems of multiple representations of 0 and the need for the end-around
carry are solved by a system called two's complement. In two's complement,
negative numbers are represented by the bit pattern which is one greater (in an
unsigned sense) than the ones' complement of the positive value. In two's-
complement, there is only one zero, represented as 00000000.

14. 2's Complement & Signed Numbers
LFU 201414

15. Signed Binary Numbers
LFU 201415
Binary Number
Representation

16. Binary Coded Decimal (BCD)
LFU 201416
Binary Coded Decimal (BCD):
In computing and electronic systems, binary-coded decimal (BCD) is
a class of binary encodings of decimal numbers where each decimal
digit is represented by a fixed number of bits, usually four or eight,

17. Gray Code
LFU 201417
 The reflected binary code, which invented by Frank
Gray, is a binary numeral system where two
successive values differ in only one bit.
 The Gray code was originally designed
to prevent false output from
electromechanical switches. Today, Gray
codes are widely used to facilitate error
correction in digital communications such
as digital terrestrial television and some
cable TV systems.

18. Binary to Gray code conversion
LFU 201418
It is easy to convert binary code to gray, by following these steps:
 (1) The M.S.B. of the gray code will be exactly equal to the first bit of
the given binary number.
 (2) Now the second bit of the code will be exclusive-or of the first
and second bit of the given binary number, i.e if both the bits are
same the result will be 0 and if they are different the result will be 1.
 (3)The third bit of gray code will be equal to the exclusive-or of the
second and third bit of the given binary number. Thus
the Binary to gray code conversion goes on. One example given
below can make your idea clear on this type of conversion.
 Let (01001) be the given binary number
 Thus the equivalent gray code is 01101.

19. Gray to Binary code conversion
LFU 201419
It is also very easy process. Just follow these steps:
 (1) The M.S.B of the binary number will be equal to the M.S.B of the
given gray code.
 (2) Now if the second gray bit is 0 the second binary bit will be same
as the previous or the first bit. If the gray bit is 1 the second binary bit
will alter. If it was 1 it will be 0 and if it was 0 it will be 1.
 (3) This step is continued for all the bits to do Gray code to binary
conversion.
 One example given below will make your idea clear.
 Let the gray code be 01101
 The binary code = (01001)

20. More Examples on Gray Code Conversion
LFU 201420

21. Excess 3 Code
LFU 201421
 It is a complementary BCD code and numeral system. It is
basically a binary code which is made by adding 3 to the
equivalent decimal of a binary number and again converting it
into binary number.
Examples:
 Excess-3 of 12 is 0001 0010 + 0011 0011 = 0100 0101 (45) .
 Excess-3 of 6 is 0110(6) + 0011(3)= 1001(9) .