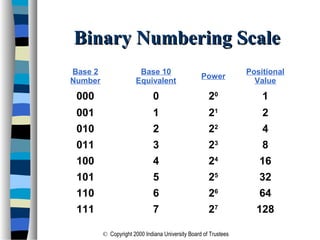
This document discusses different number systems including binary, octal, hexadecimal and decimal. It explains how to convert between these number systems using division and multiplication algorithms. It also covers complementary arithmetic operations like 1's and 2's complement. Finally, it discusses floating point number representation and sources of computational errors.