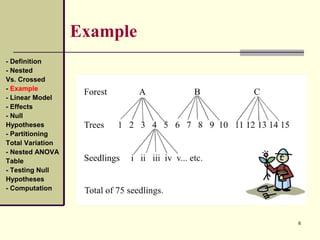
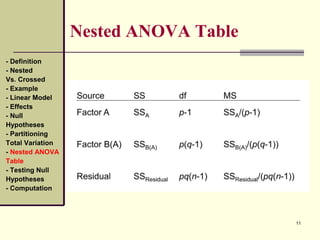
This document discusses nested designs in experiments. It defines nested designs as those where levels of one factor (B) are nested within or occur only with levels of another factor (A). An example is given of a forest genetics study measuring tree seedling height where seeds come from trees nested within different forests. The document outlines the linear model, effects, null hypotheses, partitioning variation, nested ANOVA table, testing hypotheses, and computations for a nested design.

1. Presented by:
Hossein Ahmadi
Behzad Hosseinzadeh
Supervisor: Dr.Riahi
DESIGN OF EXPERIMENTS
NESTED DESIGNS
Spring 2015 numbers of slides: 19

2. 2
Definition
Nested design is a research design in which
levels of one factor (say, Factor B ) are
hierarchically subsumed under (or nested
within) levels of another factor (say, Factor A ).
As a result, assessing the complete combination
of A and B levels is not possible in a nested
design.
- Definition
- Nested
Vs. Crossed
- Example
- Linear Model
- Effects
- Null
Hypotheses
- Partitioning
Total Variation
- Nested ANOVA
Table
- Testing Null
Hypotheses
- Computation

3. 3
Nested Vs. Crossed
Factors A and B are considered crossed if
Every level of B occurs with every level of A
A factorial model involves crossed factors
- Definition
- Nested
Vs. Crossed
- Example
- Linear Model
- Effects
- Null
Hypotheses
- Partitioning
Total Variation
- Nested ANOVA
Table
- Testing Null
Hypotheses
- Computation

4. 4
Nested Vs. Crossed
Factors A and B considered nested if:
Levels of B occur with only one level of A
- Definition
- Nested
Vs. Crossed
- Example
- Linear Model
- Effects
- Null
Hypotheses
- Partitioning
Total Variation
- Nested ANOVA
Table
- Testing Null
Hypotheses
- Computation

5. 5
Example
For example, consider a typical
provenance study where a forest
geneticist collects 5 seeds from 5
superior trees in each of 3 forests. The
seeds are germinated in a greenhouse
and the seedlings are
measured for height
growth. Graphically,
the design would look
like this...
- Definition
- Nested
Vs. Crossed
- Example
- Linear Model
- Effects
- Null
Hypotheses
- Partitioning
Total Variation
- Nested ANOVA
Table
- Testing Null
Hypotheses
- Computation

6. 6
Example
- Definition
- Nested
Vs. Crossed
- Example
- Linear Model
- Effects
- Null
Hypotheses
- Partitioning
Total Variation
- Nested ANOVA
Table
- Testing Null
Hypotheses
- Computation

7. 7
Linear Model
- Definition
- Nested
Vs. Crossed
- Example
- Linear Model
- Effects
- Null
Hypotheses
- Partitioning
Total Variation
- Nested ANOVA
Table
- Testing Null
Hypotheses
- Computation

8. 8
Null Hypotheses
- Definition
- Nested
Vs. Crossed
- Example
- Linear Model
- Effects
- Null
Hypotheses
- Partitioning
Total Variation
- Nested ANOVA
Table
- Testing Null
Hypotheses
- Computation

9. 9
Null Hypotheses
- Definition
- Nested
Vs. Crossed
- Example
- Linear Model
- Effects
- Null
Hypotheses
- Partitioning
Total Variation
- Nested ANOVA
Table
- Testing Null
Hypotheses
- Computation

10. 10
Partitioning Total Variation
- Definition
- Nested
Vs. Crossed
- Example
- Linear Model
- Effects
- Null
Hypotheses
- Partitioning
Total Variation
- Nested ANOVA
Table
- Testing Null
Hypotheses
- Computation

11. 11
Nested ANOVA Table
- Definition
- Nested
Vs. Crossed
- Example
- Linear Model
- Effects
- Null
Hypotheses
- Partitioning
Total Variation
- Nested ANOVA
Table
- Testing Null
Hypotheses
- Computation

12. 12
Testing Null Hypotheses
- Definition
- Nested
Vs. Crossed
- Example
- Linear Model
- Effects
- Null
Hypotheses
- Partitioning
Total Variation
- Nested ANOVA
Table
- Testing Null
Hypotheses
- Computation

13. 13
Computation
- Definition
- Nested
Vs. Crossed
- Example
- Linear Model
- Effects
- Null
Hypotheses
- Partitioning
Total Variation
- Nested ANOVA
Table
- Testing Null
Hypotheses
- Computation

14. 14
Computation
A B C D E Forest
1 2 3 4 5 6 7 8 9 10 Tree
15.8 13.9 18.5 17.9 12.3 14 19.5 18.7 16 15.8
Rep15.6 14.2 18 18.1 13 13.1 17.5 19 15.7 15.6
16 13.5 18.4 17.4 12.7 13.5 19.1 18.8 16.1 16.3
15.8 13.87 18.3 17.8 12.67 13.54 18.7 18.83 15.93 15.9
14.83 18.05 13.1 18.77 15.93
16.13
- Definition
- Nested
Vs. Crossed
- Example
- Linear Model
- Effects
- Null
Hypotheses
- Partitioning
Total Variation
- Nested ANOVA
Table
- Testing Null
Hypotheses
- Computation

15. 15
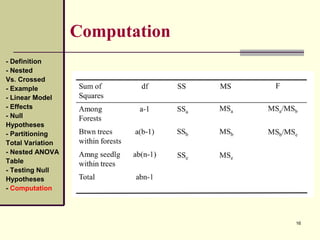
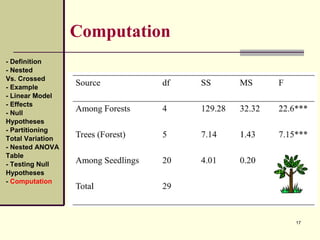
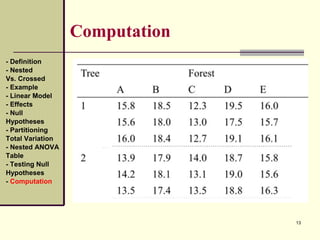
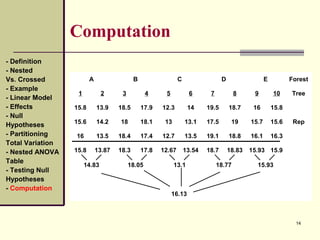
Computation
SSA = 2 x 3 [(16.13-14.83)2
+ (16.13-18.05)2
+ (16.13-13.1)2
+ (16.13-18.77)2
+ (16.13-15.93)2
]
= 129.28
SS(A)B = 3 [(15.8-14.83)2
+ (13.87-14.83)2
+ (18.3-18.05)2
+
(17.8-18.05)2
+ (12.67-13.1)2
+ (13.54-13.1)2
+
(18.7-18.77)2
+ (18.83-18.77)2
+ (15.93-15.93)2
+
(15.9-15.93)2
]
= 7.4
SSWerror = 4.01
TSS = 140.69
- Definition
- Nested
Vs. Crossed
- Example
- Linear Model
- Effects
- Null
Hypotheses
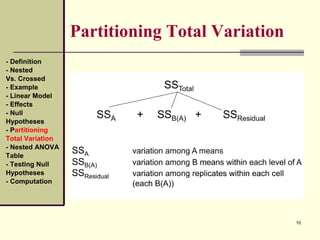
- Partitioning
Total Variation
- Nested ANOVA
Table
- Testing Null
Hypotheses
- Computation

16. 16
Computation
- Definition
- Nested
Vs. Crossed
- Example
- Linear Model
- Effects
- Null
Hypotheses
- Partitioning
Total Variation
- Nested ANOVA
Table
- Testing Null
Hypotheses
- Computation

17. 17
Computation
- Definition
- Nested
Vs. Crossed
- Example
- Linear Model
- Effects
- Null
Hypotheses
- Partitioning
Total Variation
- Nested ANOVA
Table
- Testing Null
Hypotheses
- Computation