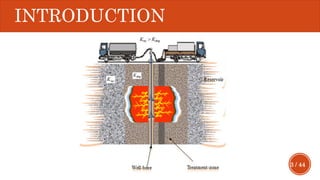
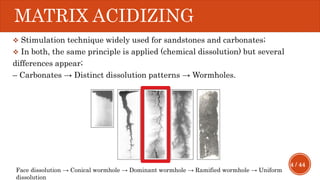
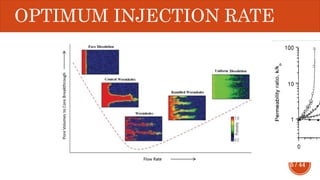
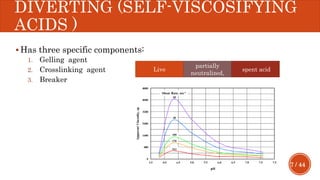
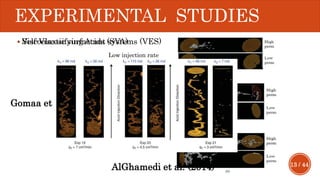
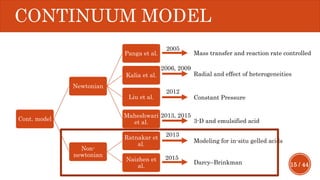
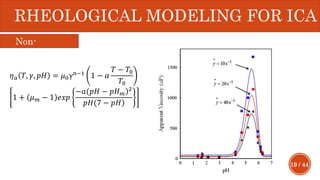
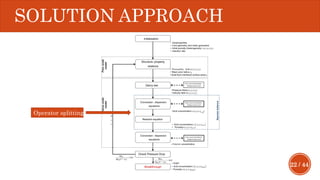
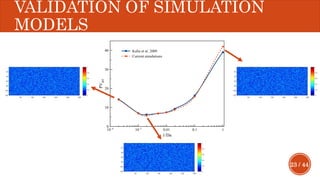
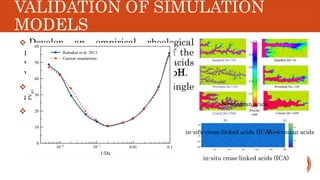
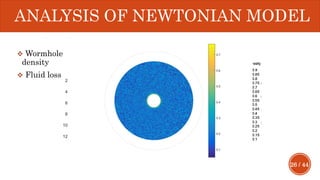
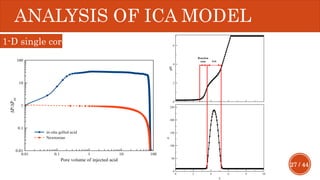
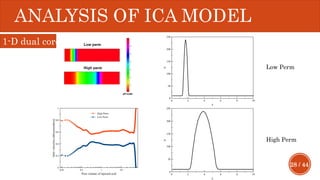
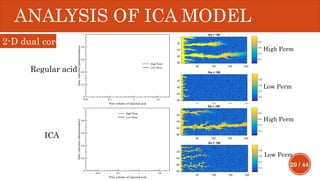
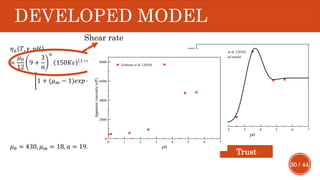
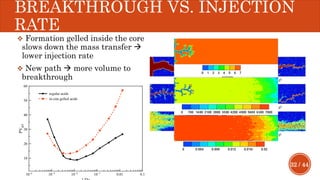
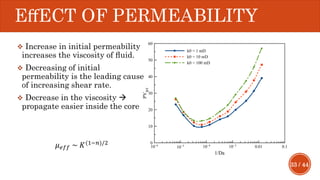
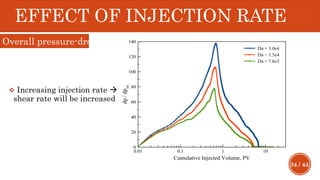
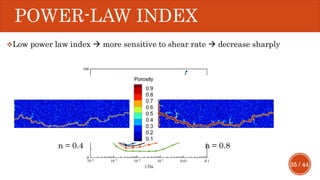
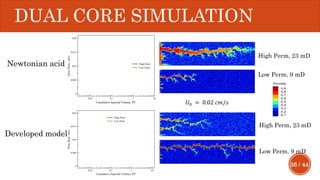
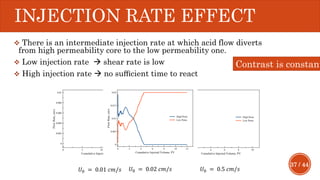
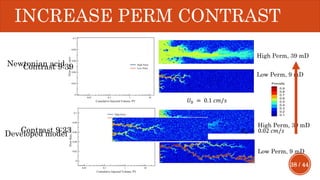
This document presents a developed model for predicting the performance of carbonate matrix acidizing. It begins with an introduction and literature review on experimental and mathematical modeling studies of matrix acidizing. It then describes the development of a continuum model using Darcy's law to model acid transport and reaction in porous media. The model accounts for non-Newtonian rheology of in-situ crosslinked acids. Results are presented on wormhole formation and the effects of injection rate, permeability, and permeability contrast using the developed model. Conclusions drawn include how rheology parameters influence acid diversion. Recommendations include extending the model to include polymer filtration effects.

1. PRESENT A DEVELOPED MODEL FOR
PREDICTING PERFORMANCE OF
CARBONATE MATRIX ACIDIZING
Presented by:
Behzad Hosseinzadeh
Supervisors:
Dr. Behzad Rostami,
Dr. Shahab Ayatollahi
Dr. Mohammad Bazargan Summer 2016

2. 2 / 44
 Introduction
 Literature review
 Continuum model
 Results
 Conclusions
 Recommendations
INTRODUCTION

3. 3 / 44
INTRODUCTION

4. 4 / 44
MATRIX ACIDIZING
 Stimulation technique widely used for sandstones and carbonates;
 In both, the same principle is applied (chemical dissolution) but several
differences appear;
– Carbonates → Distinct dissolution patterns → Wormholes.
Face dissolution → Conical wormhole → Dominant wormhole → Ramified wormhole → Uniform
dissolution

5. 5 / 44
OPTIMUM INJECTION RATE

6. 6 / 44
DIVERTING
 Acid-removable damage is not present
 If it is present it is not fully contacted
o Acid does not go where it needs to go
Before acid treatment After acid treatment
(without diverter)

7. 7 / 44
DIVERTING (SELF-VISCOSIFYING
ACIDS )
 Has three specific components:
1. Gelling agent
2. Crosslinking agent
3. Breaker
Live
partially
neutralized,
spent acid

8. 8 / 44
DIVERTING (VES)

9. 9 / 44
MODELING
 High cost
 Safety
 Upscaling

10. 10 / 44
 Introduction
 Literature review
 Continuum model
 Results
 Conclusions
 Recommendations
LITERATURE
REVIEW

11. 11 / 44
LITERATURE REVIEW
Experimental
• Williams et al. (1979)
• Daccord et al. (1987, 1993a, 1993b)
• Lund et al. (1973, 1975)
• Hoefner and Fogler (1989)
• Bazin et al. (1995)
• Fredd and Fogler (1998)
• Golfier et al. (2002)
• Taylor et al. 2002
• Nasr-El-Din et al. (2006, 2007)
• Ziauddin and Bize (2007)
• Omer Izgec (2009)
• Gomaa et al. (2010, 2011)
• Rabie et al. (2012)
• Mehdi Gommem (2015)
Mathematical
• Capillary Tube Model: Hung et al.
(1997), Buijse (1997), Huang et al.
(1999, 2000)
• Fractal and Dimensionless: Dacord
(1993), Kurmayr (1992), Pichler et
al. (1992) Fred and Fogler (1999)
• Network Model: Hoefner and Fogler
(1988), Fred and Fogler (1998)
• Continuum (Averaged) Model:
Newtonian: Golfier et al. (2002),
Panga (2005), Kalia (2005,2009),
Cohen et al. (2008), Liu et al.
(2012), Maheshwari (2013, 2015),
Gommem (2015)
Non-Newtonian: Ratnakar et al.
(2013), Naizhen et al. (2015)

12. 12 / 44
EXPERIMENTAL STUDIES
Newtonian Acid
Bazin (2001) Omer Izgec (2009)McDuff (2010)

13. 13 / 44
EXPERIMENTAL STUDIES
 Self-Viscosifying Acids (SVA)
Low injection rate
High injection rate
Intermediate injection rate
Gomaa et al. (2011)
 Viscoelastic surfactant systems (VES)
AlGhamedi et al. (2014)

14. 14 / 44
WORMHOLE MODELING
Capillary Tube Model
Fractal and
Dimensionless Model
Network Model
Continuum (Averaged)
Model

15. 15 / 44
CONTINUUM MODEL
Cont. model
Newtonian
Panga et al.
Kalia et al.
Liu et al.
Maheshwari
et al.
Non-
newtonian
Ratnakar et
al.
Naizhen et
al.
Mass transfer and reaction rate controlled
Radial and effect of heterogeneities
Constant Pressure
3-D and emulsified acid
Modeling for in-situ gelled acids
Darcy–Brinkman
2005
2006, 2009
2012
2013, 2015
2013
2015

16. 16 / 44
 Introduction
 Literature review
 Continuum model
 Results
 Conclusions
 Recommendations
CONTINUUM MODEL

17. 17 / 44
DARCY SCALE MODEL
Darcy Equation𝐔 = −
1
𝜇
𝐊 . 𝛁𝑃,
Continuity
𝜕𝜀
𝜕𝑡
+ 𝛁. 𝑼 = 0,
Acid Transport
𝜕(𝜀𝐶𝑓)
𝜕𝑡
+ 𝛁. 𝐔𝐶𝑓 = 𝛁. 𝜀𝐃 𝐞. 𝛁𝐶𝑓 − 𝑘 𝑐 𝑎 𝑣(𝐶𝑓 − 𝐶𝑠),
Reaction Rate → first order
irreversible reaction
𝑘 𝑐 𝐶𝑓 − 𝐶𝑠 = 𝑅(𝐶𝑠), 𝑅 𝐶𝑠 = 𝑘 𝑠 𝐶𝑠
Porosity Variation
𝜕𝜀
𝜕𝑡
=
𝑅(𝐶𝑠)𝑎 𝑣 𝛼
𝜌𝑠
,
Newtonian

18. 18 / 44
PORE SCALE MODEL
 the quantities 𝑲, 𝑫 𝒆 , 𝒌 𝒄 , and 𝒂 𝒗 obtained from such a
calculation can be used as inputs from the pore scale model
to the Darcy scale model.
 Structure-Property Relations (𝑲, 𝒂 𝒗)
 Mass-Transfer Coefficient (𝒌 𝒄)
Fluid Phase Dispersion Coefficients (𝑫 𝒆)
Carman-Kozney relation
Permeability change
𝐾
𝐾0
=
𝜀
𝜀0
(
𝜀(1 − 𝜀0)
𝜀0(1 − 𝜀)
)2𝛽
,
Pore radius change
𝑟𝑝
𝑟0
=
𝐾𝜀0
𝐾0 𝜀
,
Interfacial area change
𝑎 𝑣
𝑎0
=
𝜀𝑟0
𝜀0 𝑟𝑝
,
𝑆ℎ =
2𝑘 𝑐 𝑟 𝑝
𝐷 𝑚
= 𝑆ℎ∞ + 0.35(
𝑑ℎ
𝑥
)0.5 𝑅𝑒 𝑝
1/2
𝑆𝑐1/3,
Sc=ν/Dm
Sherwood
𝐷 𝑇 =
𝐷 𝑒𝑇
𝐷 𝑚
= 𝛼 𝑜𝑠 + 𝜆 𝑇 𝑃𝑒 𝑝, 𝑃𝑒 𝑝 =
𝑈 𝑑ℎ
𝜀𝐷 𝑚
,
𝐷 𝑥 =
𝐷 𝑒𝑋
𝐷 𝑚
= 𝛼 𝑜𝑠 + 𝜆 𝑋 𝑃𝑒 𝑝, 𝑃𝑒 𝑝=
𝑈 𝑑ℎ
𝜀𝐷 𝑚
,
Taylor-Aris

19. 19 / 44
RHEOLOGICAL MODELING FOR ICA
𝜂 𝑎 𝑇, 𝛾, 𝑝𝐻 = 𝜇0γ 𝑛−1 1 − 𝛼
𝑇 − 𝑇0
𝑇0
1 + 𝜇 𝑚 − 1 𝑒𝑥𝑝
−𝑎( )𝑝𝐻 − 𝑝𝐻 𝑚
2
)𝑝𝐻(7 − 𝑝𝐻
Non-
Newtonian

20. 20 / 44
TWO-SCALE CONTINUUM FOR ICA
𝐔 = −
1
𝜇 𝑒𝑓𝑓
𝐊. 𝛻𝑃,
൯𝜕(𝜀𝐶 𝑝
𝜕𝑡
+ 𝛻. 𝐔𝐶 𝑝 = 𝛻. 𝜀𝐃 𝐞. 𝛻𝐶𝑓 ,
𝜇 𝑒𝑓𝑓 𝑫 𝒎 = 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡
𝜇0 = 𝜇00 1 + (𝜇 𝑝0 − 1) Τ𝐶 𝑃 𝐶 𝑃,𝑖𝑛 ,
𝜇 𝑚 − 1
𝜇 𝑚𝑎𝑥 − 1
=
൯1 − ex p( − 𝛼1 Τ𝐶 𝑃 𝐶 𝑃,𝑖𝑛
)1 − ex p( − 𝛼1
Improveme
nt
Darcy
equivale
nt
Polymer
con.
Stoke-
Einstein
Existenc
e
polymer
multi-core set-
up

21. 21 / 44
BOUNDARY CONDITIONS
No flow, no flux, or periodic
No flow, no flux, or periodic
𝐶𝑓 = 𝐶 𝑝 = 0 @ 𝑡 = 0,
𝜀 𝑥, 𝑦, 𝑎, 𝑙 = 𝜀0 + 𝑓̂̂(𝑎, 𝑙) @ 𝑡 = 0,

22. 22 / 44
SOLUTION APPROACH
Operator splitting

23. 23 / 44
VALIDATION OF SIMULATION
MODELS

24. 24 / 44
VALIDATION OF SIMULATION
MODELS
 Develop an empirical rheological
model to describe the variation of the
viscosity of in-situ cross-linked acids
with temperature, shear rate and pH.
 Analyze wormhole formation in single
and dual core set-ups.
 2D and 3D
Newtonian acidsin-situ cross-linked acids (ICA)
Newtonian acids
in-situ cross-linked acids (ICA)

25. 25 / 44
 Introduction
 Literature review
 Continuum model
 Results
 Conclusions
 Recommendations
RESULTS

26. 26 / 44
ANALYSIS OF NEWTONIAN MODEL
 Wormhole
density
 Fluid loss

27. 27 / 44
ANALYSIS OF ICA MODEL
1-D single core

28. 28 / 44
ANALYSIS OF ICA MODEL
High Perm
Low Perm
1-D dual core

29. 29 / 44
ANALYSIS OF ICA MODEL
ICA
Low Perm
High Perm
Low Perm
Regular acid
High Perm
2-D dual core

30. 30 / 44
DEVELOPED MODEL
𝜂 𝑎 𝑇, 𝛾, 𝑝𝐻
=
𝜇0
12
9 +
3
𝑛
𝑛
150𝐾𝜀 Τ1−𝑛 2 𝐔 𝑛−1 1 − 𝛼
𝑇 − 𝑇0
𝑇0
ቈ1 + (𝜇 𝑚 − 1)𝑒𝑥𝑝
−𝑎( )𝑝𝐻 − 𝑝𝐻 𝑚
2
)𝑝𝐻(7 − 𝑝𝐻
𝜇0 = 430, 𝜇 𝑚 = 18, 𝑎 = 19.9, 𝑝𝐻 𝑚 = 3.6, 𝑏 = 1.4, 𝑐 = 6.6, 𝑊 = 3.2
Trust
Region
Shear rate

31. 31 / 44
POWER-LAW INDEX
2
,
2

32. 32 / 44
BREAKTHROUGH VS. INJECTION
RATE
 Formation gelled inside the core
slows down the mass transfer 
lower injection rate
 New path  more volume to
breakthrough

33. 33 / 44
EffECT OF PERMEABILITY
𝜇 𝑒𝑓𝑓 ~ 𝐾(1−𝑛)/2
 Increase in initial permeability
increases the viscosity of fluid.
 Decreasing of initial
permeability is the leading cause
of increasing shear rate.
 Decrease in the viscosity 
propagate easier inside the core

34. 34 / 44
EFFECT OF INJECTION RATE
 Increasing injection rate 
shear rate will be increased
Overall pressure-drop

35. 35 / 44
POWER-LAW INDEX
Low power law index  more sensitive to shear rate  decrease sharply
n = 0.4 n = 0.8

36. 36 / 44
DUAL CORE SIMULATION
High Perm, 23 mD
Low Perm, 9 mD
High Perm, 23 mD
Low Perm, 9 mD
𝑈0 = 0.02 𝑐𝑚/𝑠
Newtonian acid
Developed model

37. 37 / 44
INJECTION RATE EFFECT
𝑈0 = 0.01 𝑐𝑚/𝑠 𝑈0 = 0.5 𝑐𝑚/𝑠
 There is an intermediate injection rate at which acid flow diverts
from high permeability core to the low permeability one.
 Low injection rate  shear rate is low
 High injection rate  no sufficient time to react
𝑈0 = 0.02 𝑐𝑚/𝑠
Contrast is constant

38. 38 / 44
INCREASE PERM CONTRAST
Contrast 9:39
Contrast 9:23 𝑈0 = 0.02 𝑐𝑚/𝑠
𝑈0 = 0.1 𝑐𝑚/𝑠
Low Perm, 9 mD
High Perm, 39 mD
Newtonian acid
Developed model
High Perm, 39 mD
Low Perm, 9 mD

39. 39 / 44
EXPERIMENTAL
Sharif Well Stimulation Experiment

40. 40 / 44
 Introduction
 Literature review
 Continuum model
 Results
 Conclusions
 Recommendations
CONCLUSIONS

41. 41 / 44
CONCLUSIONS
 New in-situ gelled  higher 𝑃𝑉𝐵𝑇 and thinner compared to regular acid.
 Remaining viscosity at high  the key to block-off the high
permeability core.
 Rheology parameters  play the most important role to divert acid.
 There is a intermediate injection rate to achieve diversion.
 Increasing permeability contrast  increase optimum injection rate to
divert acid.
 Increasing permeability contrast  wormhole shape to uniform shape

42. 42 / 44
 Introduction
 Literature review
 Continuum model
 Results
 Conclusions
 Recommendations
RECOMMENDATIO
NS

43. 43 / 44
RECOMMENDATIONS
 The current model can be extended to include the effects of filtration
or adsorption/desorption of polymers and cross-linkers. In addition,
all additives (polymer, cross-linker and breakers) have been assumed
as a single species in the model, i.e. they are assumed to have similar
properties.
 In the present work, we have assumed that the reaction is
irreversible and occurs in a single step, which might not be the case
for slow reacting acids. Thus, another important extension of the
work is to include the multistep chemistry and effect of ionic-
equilibria on the dissolution process.
 Other possible extensions include the analysis of radial flow and
field scale operation to estimate wormhole properties such as density,
length, fractal dimension, etc. in extended domains.
 Extension to other diverting acids such as viscoelastic acids (VES).

44. 44 / 44
THANK YOU FOR YOUR
KIND ATTENTION