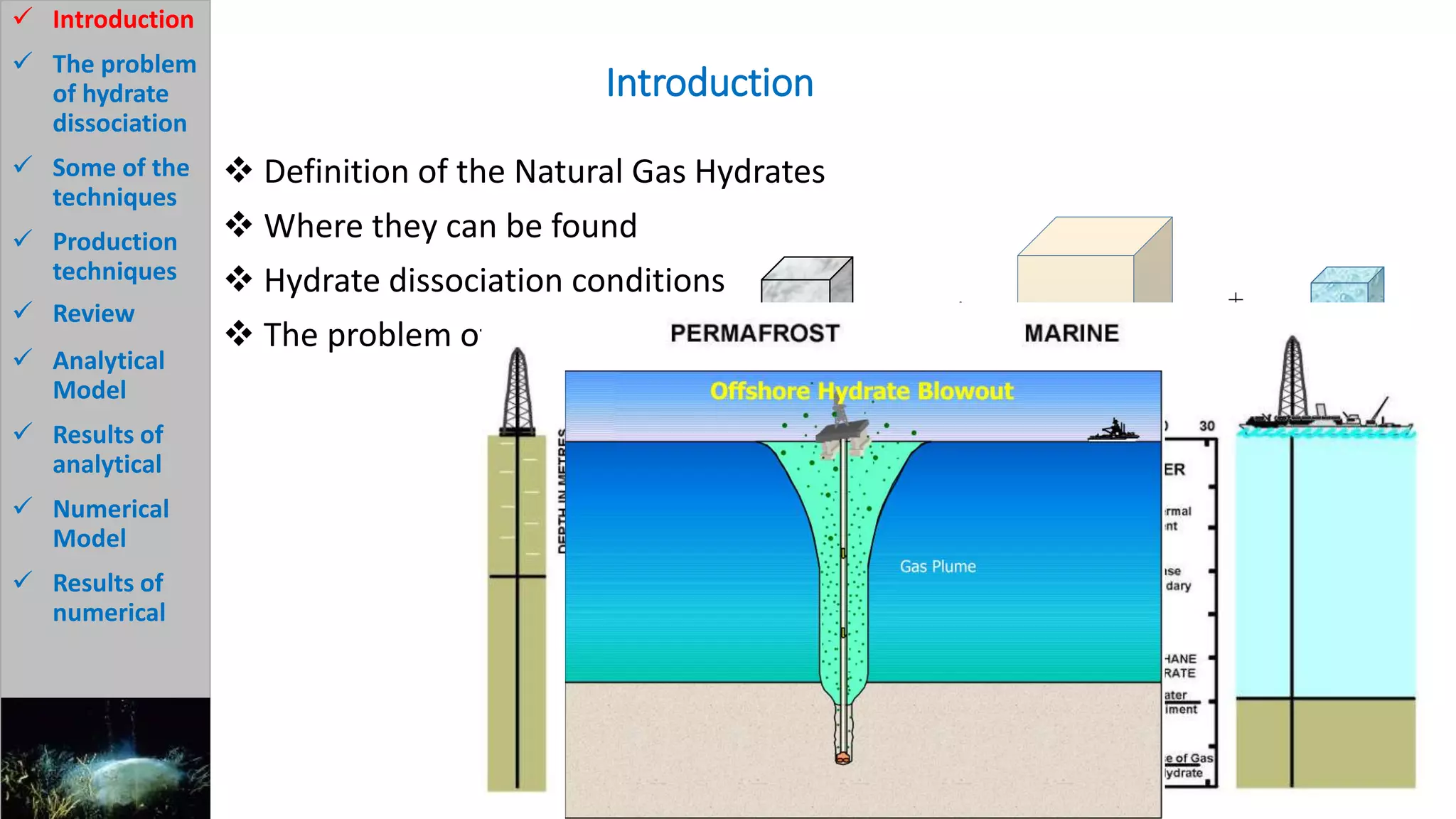
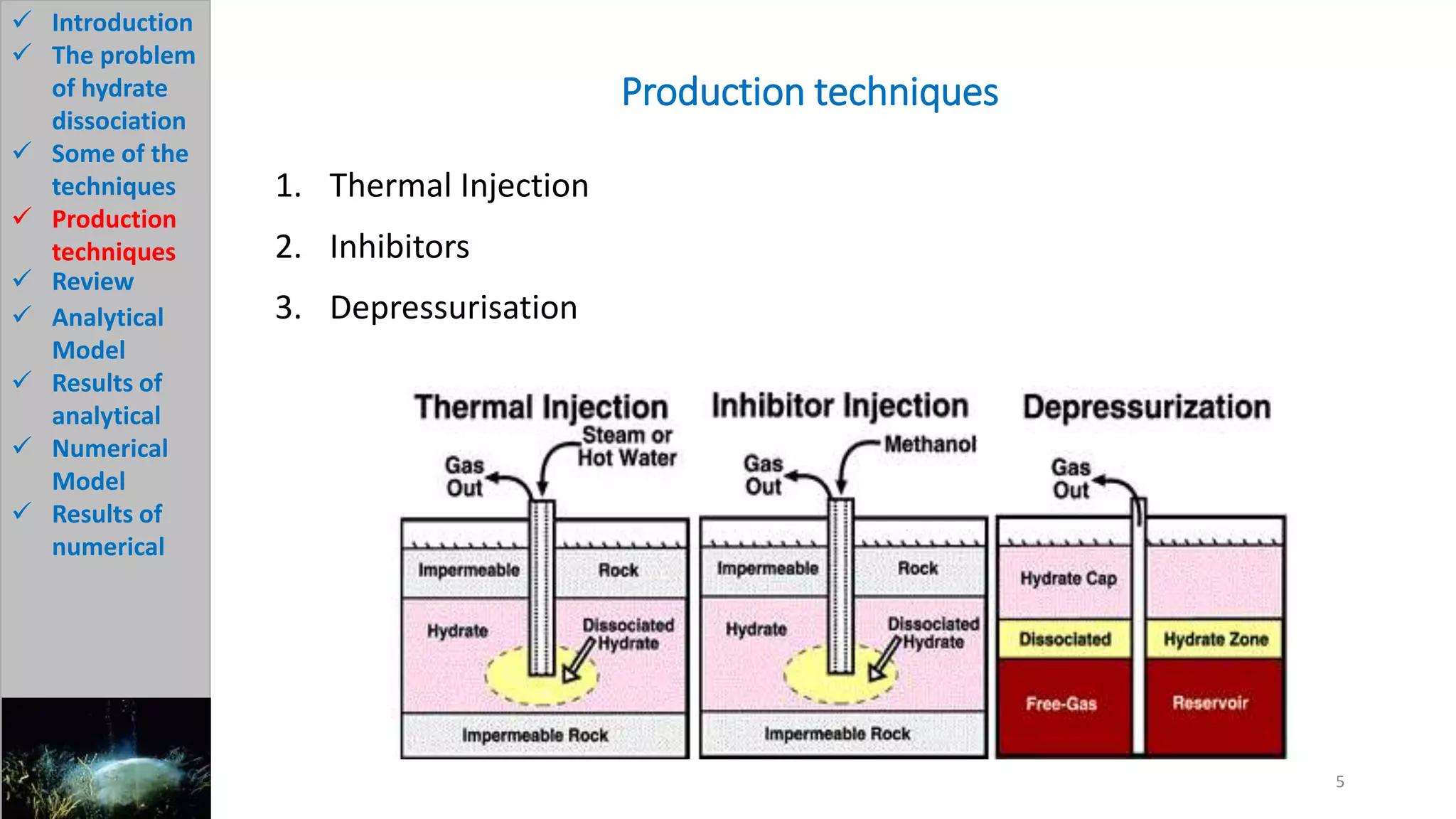
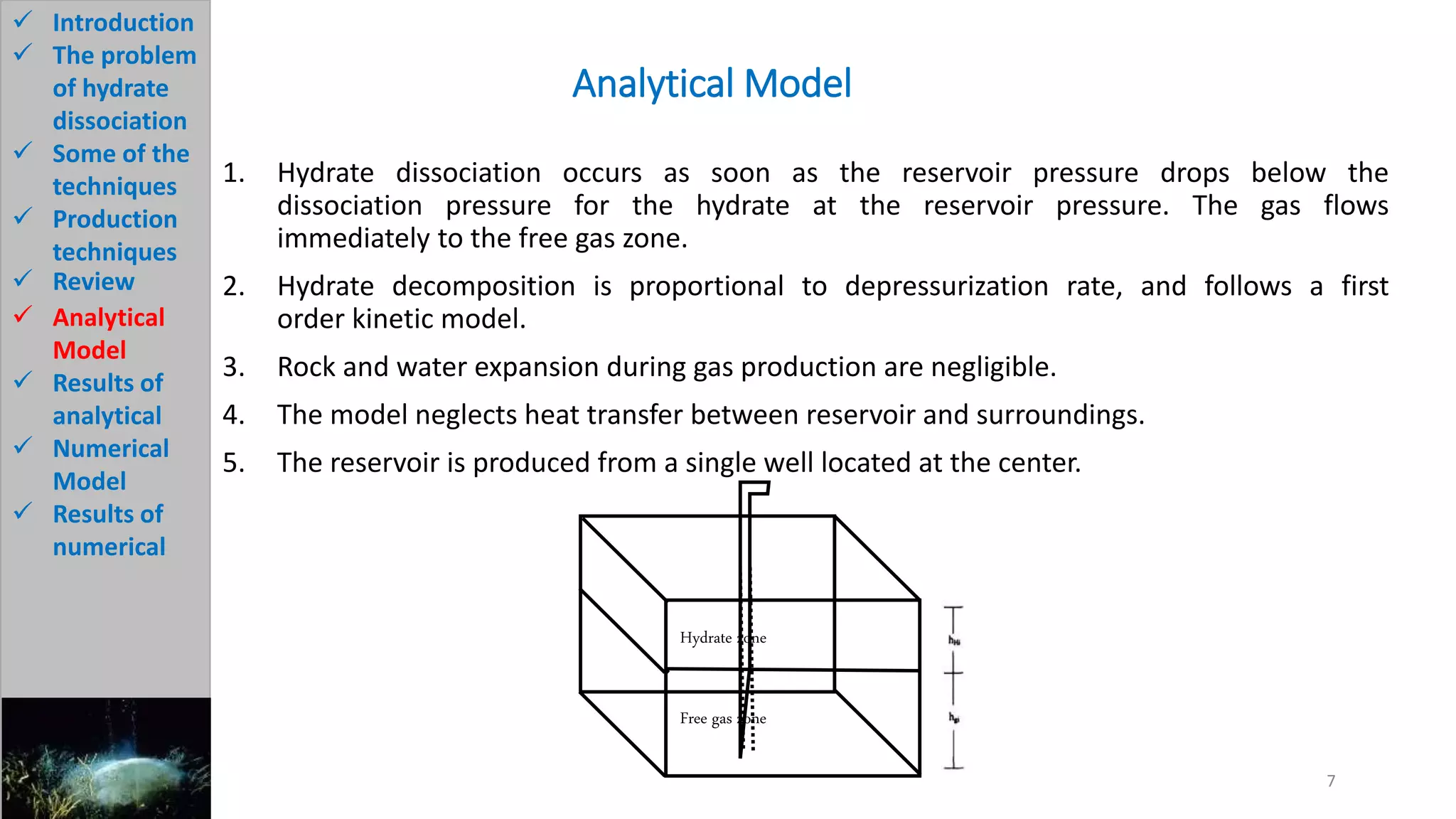
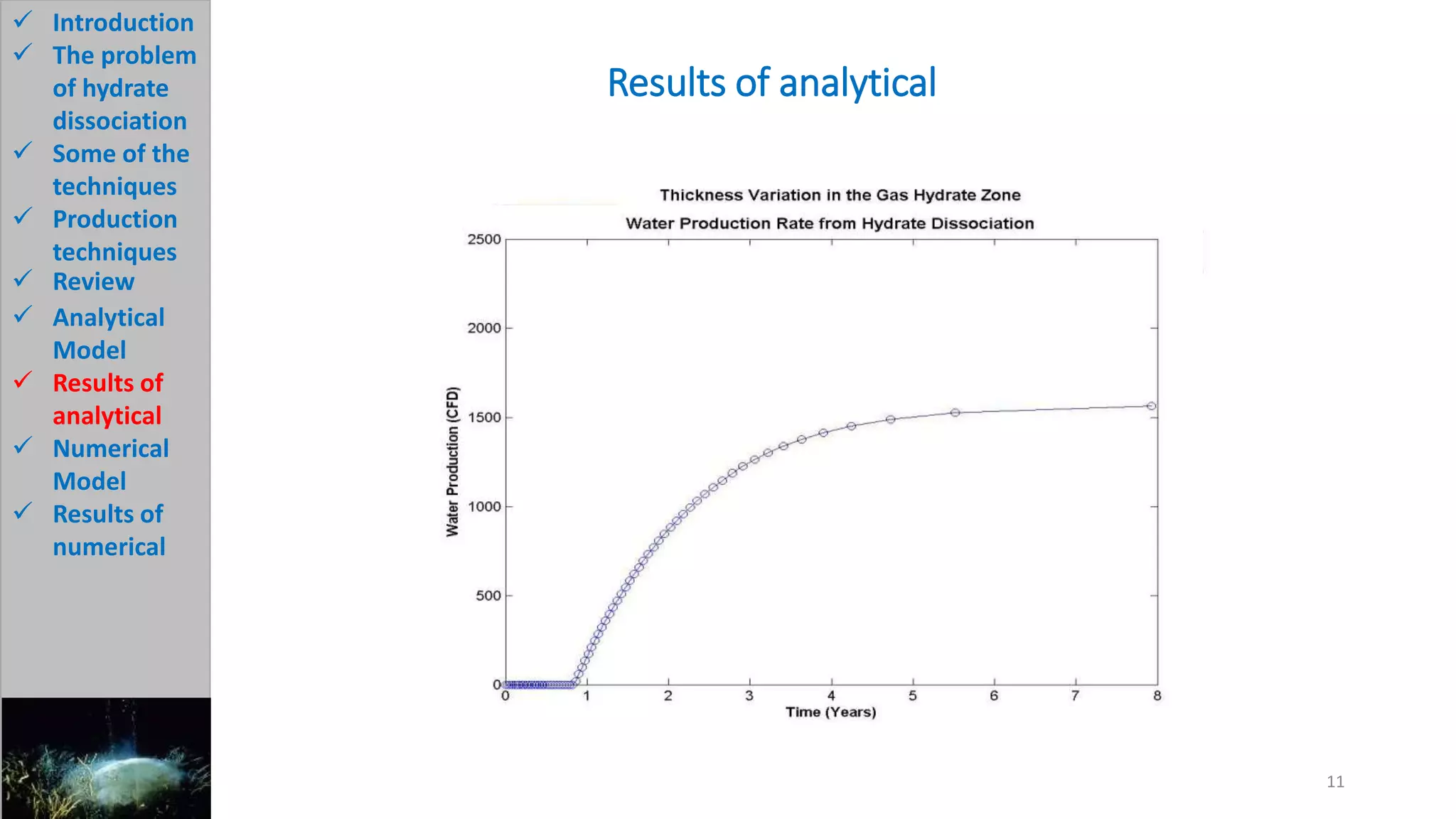
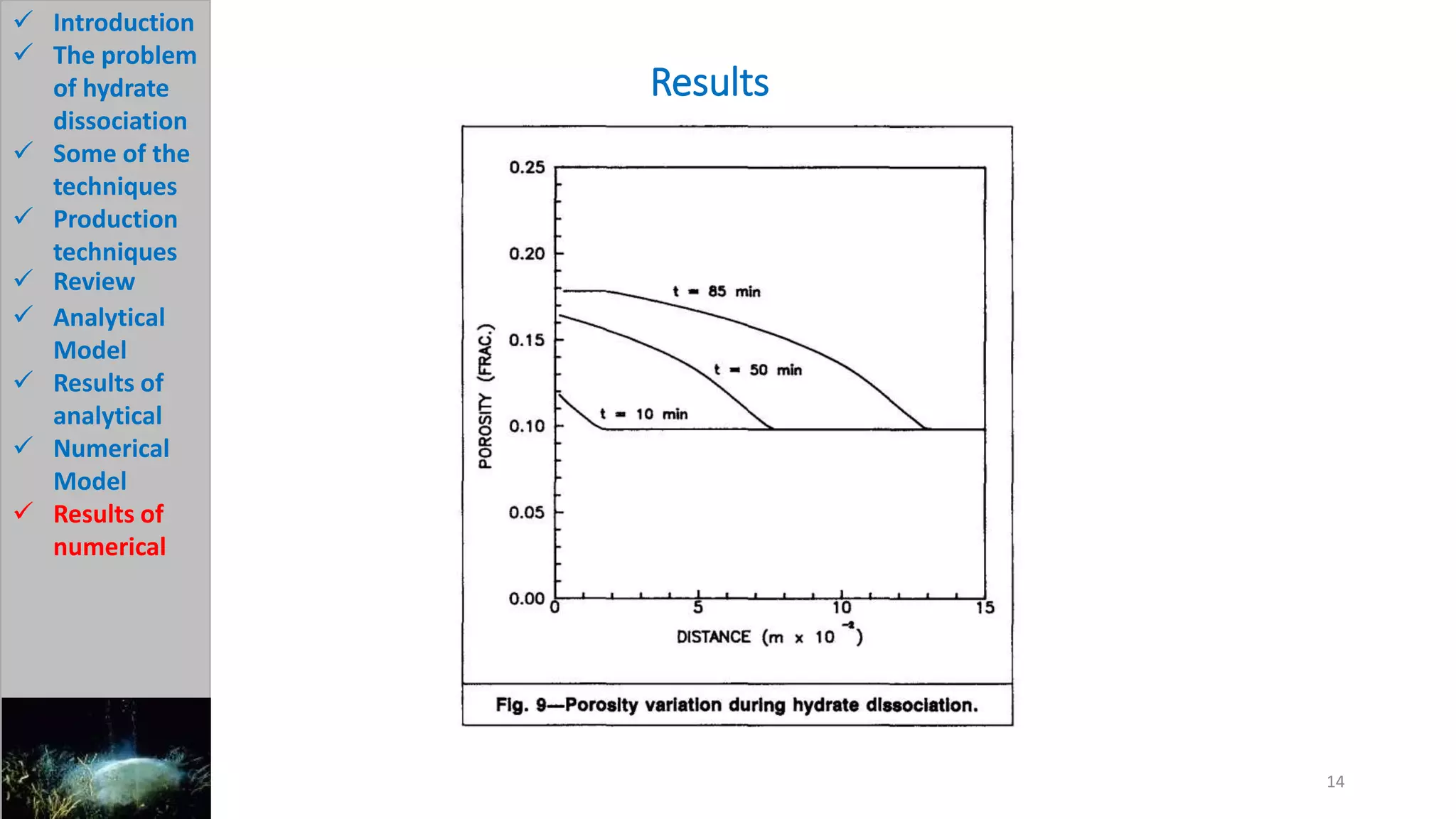
1) The document presents numerical and analytical models for simulating natural gas production from methane hydrate dissociation. 2) It describes the problem of hydrate dissociation in wells, which can cause wellbore collapse if not controlled. Various techniques to avoid this such as cooling drilling fluid or increasing mud weight are also discussed. 3) The analytical model assumes hydrate dissociation occurs immediately when pressure drops below threshold and follows first-order kinetics. The numerical model sets up governing equations to simulate two-phase flow and permeability changes during dissociation.

1. Numerical and analytical solution
for natural gas production
from methane hydrate dissociation
By:
Behzad Hosseinzadeh

2. Introduction
 Definition of the Natural Gas Hydrates
 Where they can be found
 Hydrate dissociation conditions
 The problem of hydrate dissociation
2
+
1m3
164m3
0.8m3
STP
 Introduction
 The problem
of hydrate
dissociation
 Some of the
techniques
 Production
techniques
 Review
 Analytical
Model
 Results of
analytical
 Numerical
Model
 Results of
numerical

3. The problem of hydrate dissociation
 hydrate dissociation → gasification of the drilling fluid → lowering
of mud density → changes mud rheology → lowering hydrostatic
pressure → further dissociation → wellbore enlargement and
wellbore collapse
 hydrate dissociation → change of mechanical and petrophysical
properties of the sediment → increase in permeability →
reduction in strength of the sediments
3
 Introduction
 The problem
of hydrate
dissociation
 Some of the
techniques
 Production
techniques
 Review
 Analytical
Model
 Results of
analytical
 Numerical
Model
 Results of
numerical

4. Some of the techniques adopted so far to avoid the risks of drilling in HBS
1. Cooling the drilling fluid
2. Increasing the mud weight
3. Adding chemical inhibitors and kinetic additives to the drilling fluid
4. Accelerating drilling by running casing immediately after hydrate are
encountered and using a cement of high strength and low heat of
hydration
4
 Introduction
 The problem
of hydrate
dissociation
 Some of the
techniques
 Production
techniques
 Review
 Analytical
Model
 Results of
analytical
 Numerical
Model
 Results of
numerical

5. Production techniques
1. Thermal Injection
2. Inhibitors
3. Depressurisation
5
 Introduction
 The problem
of hydrate
dissociation
 Some of the
techniques
 Production
techniques
 Review
 Analytical
Model
 Results of
analytical
 Numerical
Model
 Results of
numerical

6. Review of Hydrate Reservoir Simulation Models
6
 Introduction
 The problem
of hydrate
dissociation
 Some of the
techniques
 Production
techniques
 Review
 Analytical
Model
 Results of
analytical
 Numerical
Model
 Results of
numerical
Santanu Khataniar

7. 1. Hydrate dissociation occurs as soon as the reservoir pressure drops below the
dissociation pressure for the hydrate at the reservoir pressure. The gas flows
immediately to the free gas zone.
2. Hydrate decomposition is proportional to depressurization rate, and follows a first
order kinetic model.
3. Rock and water expansion during gas production are negligible.
4. The model neglects heat transfer between reservoir and surroundings.
5. The reservoir is produced from a single well located at the center.
Analytical Model
7
 Introduction
 The problem
of hydrate
dissociation
 Some of the
techniques
 Production
techniques
 Review
 Analytical
Model
 Results of
analytical
 Numerical
Model
 Results of
numerical
Hydrate zone
Free gas zone

8. Analytical Model
8
 Introduction
 The problem
of hydrate
dissociation
 Some of the
techniques
 Production
techniques
 Review
 Analytical
Model
 Results of
analytical
 Numerical
Model
 Results of
numerical
 for a closed system, the total volumetric change must be zero
 using mass balance principles
GHi , GHr = initial and remaining gas in the form of hydrate, BgH = reservoir hydrate volumetric factor ,φ=
reservoir porosity, SWi = initial water saturation , ∆hH = change in hydrate zone thickness, Gfi , Gp , GeH =
initial free gas, total gas production and gas produced from hydrate ,Bgi , Bg = reservoir gas volumetric
factor, Wp , WeH = total water production and water produced from hydrate dissociation, hg = gas zone
thickness
 After substitution , we have

9. Analytical Model
9
 Introduction
 The problem
of hydrate
dissociation
 Some of the
techniques
 Production
techniques
 Review
 Analytical
Model
 Results of
analytical
 Numerical
Model
 Results of
numerical
 The volumes of initial free gas and initial gas in the
form of hydrates (hydrated gas) in place are given by:
 The ratio of initial free gas volume to initial hydrate volume is:
 then
 The water production rate is given by:
 The pressure derivative respect to time is
obtained from material balance equation
as:

10. Analytical Model
 Introduction
 The problem
of hydrate
dissociation
 Some of the
techniques
 Production
techniques
 Review
 Analytical
Model
 Results of
analytical
 Numerical
Model
 Results of
numerical
 This is done by using the approximation:
 Z-factor is also pressure-dependent, and can be estimated using the Hall-Yarborough
equation

11. Results of analytical
11
 Introduction
 The problem
of hydrate
dissociation
 Some of the
techniques
 Production
techniques
 Review
 Analytical
Model
 Results of
analytical
 Numerical
Model
 Results of
numerical

12. 1. The gas hydrate in our assumed simulation is SI type, without the salt consideration;
2. Two-phase flow accords with Darcy’s law, and hydrate is stagnant in porous media;
3. The absolute permeability of porous media is the function of hydrate saturation;
4. The generated gas does not dissolve in water, and without hydrate reformation;
5. The diffusion and the dispersion are neglected in mass transportation;
6. There is no ice phase during the whole dissociation;
7. isothermal hydrate
8. the hydrate-bearing sediments are rigid and do not deform during hydrate dissociation.
Numerical Model
12
 Introduction
 The problem
of hydrate
dissociation
 Some of the
techniques
 Production
techniques
 Review
 Analytical
Model
 Results of
analytical
 Numerical
Model
 Results of
numerical

13. Model
13
 Infiltration equation  Initial conditions
 Supplemental formula
 Auxiliary equation
 Introduction
 The problem
of hydrate
dissociation
 Some of the
techniques
 Production
techniques
 Review
 Analytical
Model
 Results of
analytical
 Numerical
Model
 Results of
numerical

14. Results
14
 Introduction
 The problem
of hydrate
dissociation
 Some of the
techniques
 Production
techniques
 Review
 Analytical
Model
 Results of
analytical
 Numerical
Model
 Results of
numerical

15. 15