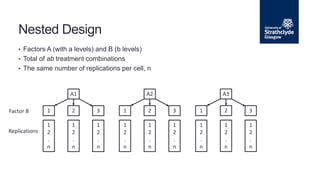
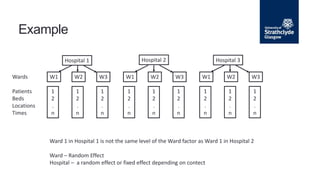
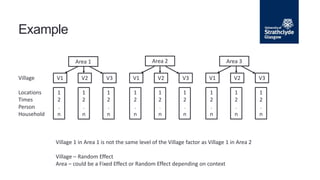
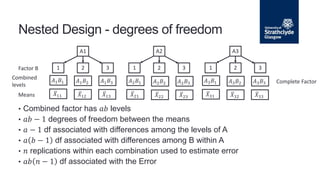
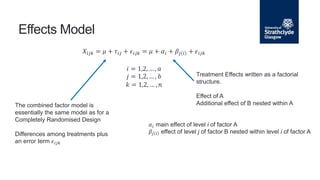
The document describes a nested analysis of variance (ANOVA) model with two factors, A and B. Factor B is nested within levels of factor A, meaning its levels are specific to each level of A. There are a levels of A and b levels of B, with n replications per combination, for a total of ab treatment combinations. The nested design partitions variance components between factors A and B and residual error. Hypotheses can be tested regarding fixed or random effects using F-tests based on mean squares from the nested ANOVA.