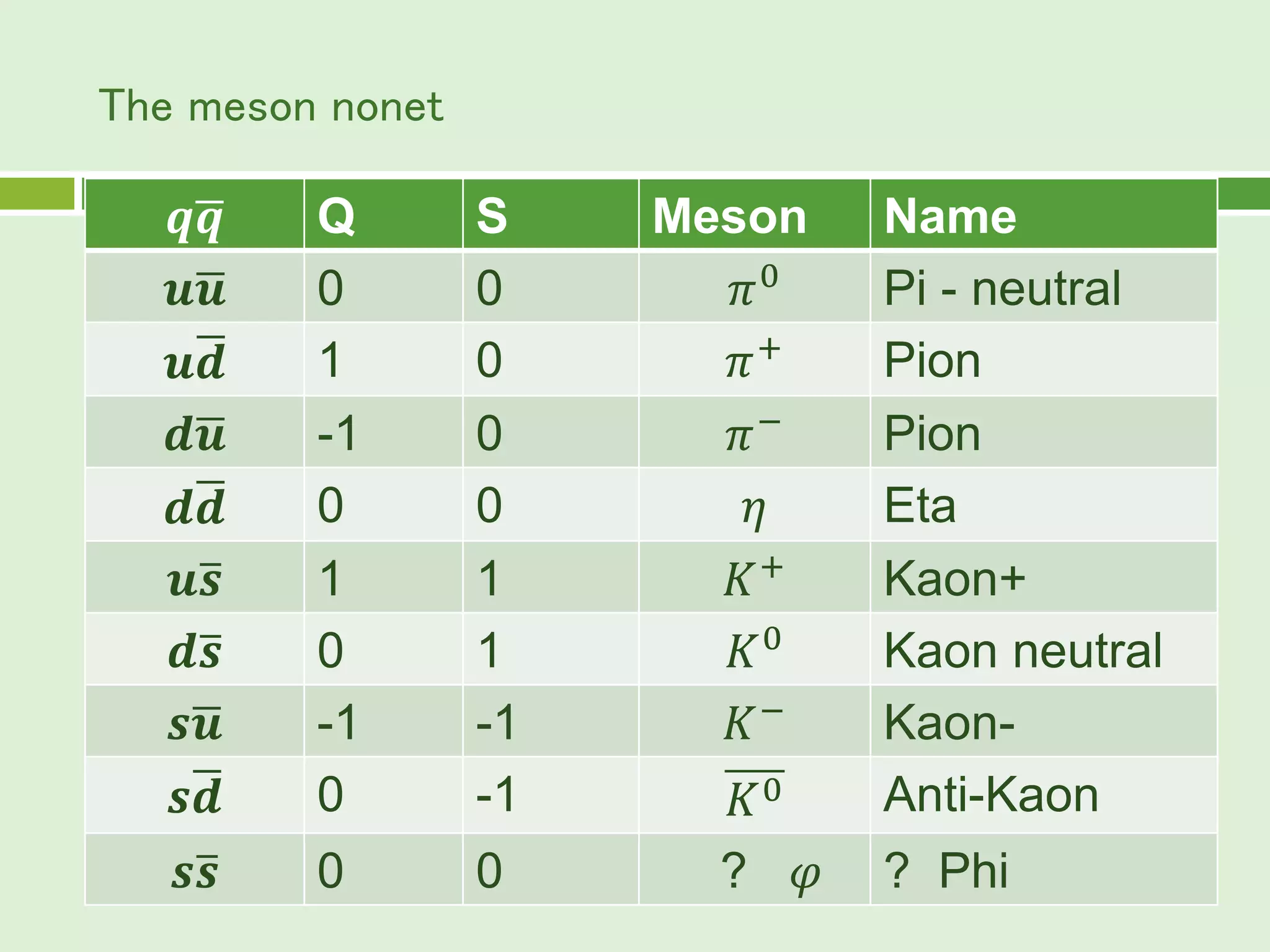
The document summarizes the quark model proposed in 1964 to describe the internal structure of hadrons such as protons and neutrons. It states that all hadrons are composed of more fundamental particles called quarks, which come in three flavors: up, down, and strange. The model was later expanded to incorporate three colors and additional quark flavors as more particles were discovered. The quark model provided explanations for experimental findings and made accurate predictions that were later verified, gaining broad acceptance.

1. THE QUARK MODEL
vidya.patil@ruparel.edu
20th August 2018

2. The Quark Model : 1964
 In 1964 Gell-Mann and Zweig independently proposed that all
hadrons are in fact composed of even more elementary
constituents, which Gell-Mann called quarks.
 The quarks come in three types (or “flavors”), forming a triangular
“Eightfold- Way” pattern
 The Up Quark 𝑢
2
3
 The Down Quark 𝑑
−1
3
 The Strange Quark 𝑠 (
−1
3
)

3. Murray Gell-Mann

4. George Zweig

5. The Quarks
 The u (for “up”) quark
carries a charge of
2
3
and
a strangeness of zero;
the d (“down”) quark
carries a charge of −
1
3
and 𝑆 = 0; the s (
“strange”) quark has
𝑄 = −
1
3
and 𝑆 = −1

6. The antiquark
 To each quark (𝑞) there corresponds an antiquark
(𝑞), with the opposite charge and strangeness.

7. The Quark Model
 The quark model represents a relatively simple picture of the
internal structure of subatomic particles and makes
predictions of their production and decay.
 It uses a minimum of adjusted quark parameters and has
great predictive power e.g. for the composite particle :
masses, magnetic moments and life times.
 There are no contradictions to this model known so far , but
few questions remains!!!

8. The Quark Model
 The quark model asserts that
 Every baryon is composed of three quarks (and
every antibaryon is composed of three antiquarks)
 Every meson is composed of a quark and an
antiquark.
 With these two rules it is easier to construct the
baryon decuplet and the meson octet.

9. Baryon decuplet
qqq Q S Baryon
uuu 2 0 Δ++.. Delta ++
uud 1 0 Δ+ ... Delta +
udd 0 0 Δ0
.. Delta neutral
ddd -1 0 Δ−... Delta -
uus 1 -1 Σ∗+... Sigma +
uds 0 -1 Σ∗0
... Sigma neutral
dds -1 -1 Σ∗−... Sigma -
uss 0 -2 Ξ∗0... Xi neutral
dss -1 -2 Ξ∗−... Xi -
sss -1 -3 Ω−…Omega -

10. The meson nonet
𝒒𝒒 Q S Meson Name
𝒖𝒖 0 0 𝜋0 Pi - neutral
𝒖𝒅 1 0 𝜋+
Pion
𝒅𝒖 -1 0 𝜋− Pion
𝒅𝒅 0 0 𝜂 Eta
𝒖𝒔 1 1 𝐾+ Kaon+
𝒅𝒔 0 1 𝐾0 Kaon neutral
𝒔𝒖 -1 -1 𝐾− Kaon-
𝒔𝒅 0 -1 𝐾0 Anti-Kaon
𝒔𝒔 0 0 ? 𝜑 ? Phi

11.  The same combination of quarks can result in a number of
different particles
 The delta-plus : Δ+
and the proton are both composed of
𝑢𝑢𝑑; the 𝜋+and the 𝜌+are both 𝑢𝑑
 This absurdity can be explained as analogy with the
hydrogen atom.
 As the hydrogen atom (electron plus proton) has many
different energy levels, so a given collection of quarks can
bind together in many different ways.

12.  However the various energy levels in the electron/proton
system are relatively close together and hence all of them
are represented as “hydrogen,”
 The energy spacings for different states of a bound quark
system are very large, and hence regarded as distinct
particles.
 Thus, in principle, an infinite number of hadrons can be
constructed out of only three quarks.

13. Problems with the Quark model
 Quark confinement :
 For reasons not yet known, quarks are absolutely confined
within baryons and mesons
 Even though all quarks are stuck inside hadrons, still, they are
accessible to experimental study.
 When a proton was probed using neutrino beams at CERN -
known as “deep inelastic scattering” , most of the incident
particles pass right through, whereas a small number bounced
back sharply.

14.  This means that the charge of the proton is
concentrated in small lumps
 However, in the case of the proton the evidence
suggests three lumps instead of one. This is a
strong support for the quark model

15. (a) In Rutherford scattering the number of particles deflected through large angles
indicates that the atom has internal structure (a nucleus). (b) In deep inelastic
scattering the number of particles deflected through large angles indicates that the
proton has internal structure (quarks). The dashed lines show what you would
expect if the positive charge were uniformly distributed over the volume of (a) the
atom, (b) the proton.

16. Mesons are quark
anti quark pairs
Baryons are quark
triplets

18. Theoretical objection to the quark model
 Quark Model appears to violate the Pauli exclusion principle.
 According to Pauli’s exclusion principle no two electrons can
occupy the same state.
 However the exclusion principle applies to all particles of half-
integer spin . In particular, the exclusion principle should apply to
quarks, which carry spin 1/2.
 ∆++
is supposed to consist of three identical u quarks in the same
state; it (and also the ∆−
(ddd) and the Ω−
(sss)) appear to be
inconsistent with the Pauli principle.

19. Along with flavour, quark got the colour( quantum no.)
 In 1964, O. W. Greenberg proposed a way out of this
dilemma
 He suggested that quarks not only come in three flavours
(u, d, and s) but each of these also comes in three colours
(“red,” “green,” and “blue,” say).
 To make a baryon, we take one quark of each colour, then
the three u’s in ∆++
are no longer identical (one is red, one
is green, and one is blue). The exclusion principle applies
only to identical particles!!

20. The November Revolution And Its Aftermath
 The November Revolution began with the discovery of a new subatomic
particle, the J/ψ meson , a particle with an unusually narrow width at
3095 MeV.
 on November 10, 1974 two groups (one, a MIT group doing experiment
on the east coast at Brookhaven National Laboratory, U.S.A. and the
other a SLAC- Berkeley group doing experiment on the west coast at
Stanford Linear accelerator centre, U.S.A) simultaneously announced the
discovery of a new particle at 3095 MeV whose lifetime was about 1000
times longer than that of other particles of comparable mass.

21. Samual Ting at Brookhaven National Laboratory, U.S.A.

22. Burton Richter of SLAC

23.  The discovery was announced by both groups together
on 11 November 1974, and the particle's name was
combined to 𝐽/𝜓 in order to acknowledge that both groups
had equal parts in its discovery.
 For this discovery, the heads of both research groups,
Burton Richter of SLAC and Samuel Ting of BNL, were
awarded the 1976 Nobel Prize in Physics.

24. Computer reconstruction of a psi-prime decay (the Mark I
detector), making a near-perfect image of the Greek letter psi.

25.  Till then mesons were discovered, and only three types of quarks:
up, down and strange were known.
 The importance of the J/ψ meson discovery is that it was the first
particle discovered that contained a quark never seen before, the
charm quark.
 In fact, this meson is a bound state of one charm quark and one
anti-charm quark.
 The existence of the charm quark was speculated as early as 1964,
but this was the first time it was actually seen in an experiment.

27.  This discovery sparked a revolution - the November
Revolution, named after the month in which the discovery
was announced - because it revealed a new path towards
understanding the structure of matter, namely, that all
hadrons, including the protons and neutrons, were actually
composite particles made of quarks.
 Before that, many physicists were highly sceptic of the quark
model, but the discovery of the J/ψ meson managed to
convince most of them of the model's validity.

28.  In the years following 1974, major advances in particle physics
were made.
 Other composite particles, which were made from a combination
of the charm quark and one or two of the up, down and strange
quarks, were discovered, which provided even more evidence for
the charm quark and the quark model.
 In 1975, two more quarks - the top and bottom - were
hypothesized, and in 1977, the bottom quark was discovered at
Fermi Lab.

29. Intermediate Vector Bosons
 There are three intermediate vector bosons, two of them
charged ( 𝑊±
) and one neutral (𝑍0
). Their masses were
calculated to be
 𝑀𝑤 = 82 ± 2 𝐺𝑒𝑉/𝑐2 and 𝑀𝑍 = 92 ± 2 𝐺𝑒𝑉/𝑐2
 In January 1983 the discovery of the W with mass
80.403 ± 0.029 𝐺𝑒𝑉/𝑐2 was reported by Carlo Rubbia’s and
five months later the same team announced discovery of
the 𝑀𝑍 = 91.188 ± 0.002 𝐺𝑒𝑉/𝑐2

30. Standard Model

31.  The Standard Model describes what matter is made of and
how it holds together. It rests on two basic ideas: all matter is
made of particles, and these particles interact with each other
by exchanging other particles associated with the
fundamental forces.
 The basic grains of matter are fermions and the force carriers
are bosons. The names of these two classes refer to their spin
– or angular momentum. Fermions have half-integer spin
whereas bosons have integer values

32. The Standard Model (SM)
 Since the sixties physicists have been looking for new particles. Up
to now about 200 particles (most of which are not fundamental)
have been discovered and categorized.
 - 6 quarks
 - 6 leptons (the best-known lepton is the electron)
 - Force carrier particles (like the photon)
 Experiments have verified the SM predictions with high precision
and the particles predicted by SM have been experimentally found.
 BUT…gravity is not included in SM.

33. Standard Model
 In the current view, all matter is made out of three
kinds of elementary particles: leptons, quarks, and
mediators.
 There are six leptons, classified according to their
charge (Q), electron number (Le, muon number (Lµ),
and tau number (L𝜏).
 They fall naturally into three families or generations

34. Standard Model

35. Lepton Classification
𝒍 𝑸 𝑳𝒆 𝑳𝝁 𝑳𝝉
First
Generation
𝑒
𝜈𝑒
−1
0
1
1
0
0
0
0
Second
Generation
𝜇
𝜈𝜇
−1
0
0
0
1
1
0
0
Third
Generation
𝜏
𝜈𝜏
−1
0
0
0
0
0
1
1

36. There are six antileptons, with all the signs
reversed.
The positron, for example, carries a charge
of +1 and an electron number - 1.
So there are really 12 leptons

37. Quark Classification
There are six “flavors” of quarks, which are
classified according to charge (Q),
strangeness (S), charm (C), beauty (B), and
truth (T).
The quarks also fall into three generations

38. Quark Classification
𝒒 𝑸 𝑫 𝑼 𝑺 𝑪 𝑩 𝑻
First
Generation
𝑑
𝑢
− 1
3
2
3
−1
0
0
1
0
0
0
0
0
0
0
0
Second
Generation
𝑠
𝑐
− 1
3
2
3
0
0
0
0
−1
0
0
1
0
0
0
0
Third
Generation
𝑏
𝑡
− 1
3
2
3
0
0
0
0
0
0
0
0
−1
0
0
1

39.  For every particle there exists its antiparticle and
hence we have six antiquarks.
 All signs are reversed in the table of antiquarks.
 Every quark and antiquark comes in three colours,
so there are ( 6 × 3 = 18 for quarks 𝑎𝑛𝑑 18 for
antiquarks) 36 of them in all.

40. Mediators
 Every interaction has its mediators
 Photon for the electro- magnetic force
 Two W’s and a Z for the weak force
 strong force? Pion ??
 The discovery of heavy mesons indicated that, protons and
neutrons could now exchange rho’s and eta’s and K’s and
phi’s and all the rest of them.

41.  The quark model suggested that the mediator can be complicated
and the particle which is exchanged between two quarks, in a
strong process is called the gluon, and in the Standard Model there
are eight gluons.
 The gluons themselves carry colour, and therefore can not exist as
isolated particles.
 We can detect gluons only within hadrons, or in colourless
combinations with other gluons (glueballs).
 The deep inelastic scattering experiments showed that roughly
half the momentum of a proton is carried by electrically neutral
constituents, presumably gluons

42.  Quark “confinement” disallows the presence of
free quarks. Only “white” hadrons are allowed.
This is a property of the strong interactions.
 But what happens when a quark-antiquark pair is
stretched?
 Answer: The colour force field is stretched, until it
“snaps”, producing new quarks

44. The three generations of quarks and leptons, in order of
increasing mass.

45. Generations of Matter
 Mass increases from first
generation to the next
 Going down in each
generation, the charges are:
+2/3, -1/3, 0, -1
 These are all in multiples of
the elementary charge

46. The Fundamental Building Blocks

48. The Four Fundamental Forces
These forces include interactions that are
attractive or repulsive, decay and annihilation.
Strong Weak
Electromagnetic Gravity

49. Force Strength Theory Mediator
Strong 10 Chromodynamics Gluon
Electromagnetic 10−2
Electrodynamics Photon
Weak 10−13 Flavordynamics W and Z
Gravitational 10−42 Geometrodynamics Graviton

50. The Strong Force
 The strongest of the 4 forces
 Is only effective at distances less than 10-15
meters (about the size of the nucleus)
 Holds quarks together
 This force is carried by gluons

51. Strong Force
 Protons and neutrons are bound together in the nucleus of
an atom
 This is due to the residual strong force that is binding the
quarks together in each of the baryons

52.  The strong interaction is hypothesized to be mediated by
massless particles called gluons, those are exchanged between
quarks, antiquarks, and other gluons.
 Gluons, in turn, are thought to interact with quarks and
gluons as all carry a type of charge called colour charge.
 Colour charge is analogous to electromagnetic charge, but it
comes in three types rather than one (± red, ± green, ± blue)
that results in a different type of force, with different rules of
behaviour.
 These rules are detailed in the theory of quantum
chromodynamics (QCD), which is the theory of quark-gluon
interactions.

53. Strong force: gluons
Gluons interact with quarks Gluons interact with other gluons

54. Masters of Quantum Mechanics
Paul Dirac

55. Quantum Mechanics
 The word “quantum” (Latin, “how much”) refers to a discrete unit
that quantum theory assigns to certain physical quantities, such as
the energy of an atom at rest, or the electric charge, angular
momenta etc..The discrete values of these physical quantities are
identified by quantic numbers.
 The relativistic formulation of Quantum Mechanics was done by
P.A.M. Dirac in 1928, who also predicted the existence of the
positron and antimatter.

56. Quantic numbers
Spin: In quantum mechanics the spin of a particle is related to an
angular momentum which has non-classical features. It can not be
associated to a rotation, but only refers to the presence of angular
momentum.
Isospin: It is a quantum number related to the strong
interaction, it was introduced to explain the symmetry in particles
strongly interacting and led to the discovery and understanding of
quarks (Yang-Mills theory).

57. Contd…
Flavour quantic numbers: specific numbers for
different particles species, as the leptonic and barionic number, or
charm, strangeness, bottomness, topness.
Electric charge
Conservation laws: the occurrence or not of the
different decays and interactions is governed by conservation laws
of the quantic numbers.

58. 58
Conservation Laws and Symmetries
 Physicists like to have clear rules or laws that determine
whether a certain process can occur or not.
 It seems that everything occurs in nature that is not forbidden.
 Certain conservation laws are already familiar from our study
of classical physics. These include mass-energy, charge, linear
momentum, and angular momentum.
 These are absolute conservation laws: they are always obeyed.

59. 59
Additional Conservation Laws
 These are helpful in understanding the many
possibilities of elementary particle interactions.
 Some of these laws are absolute, but others may be
valid for only one or two of the fundamental
interactions.

60. 60
Baryon Conservation
 In low-energy nuclear reactions, the number of nucleons is always
conserved.
 Empirically this is part of a more general conservation law .
 It assignes a new quantum number called baryon number that has the value
B = +1 for baryons and −1 for antibaryons, and 0 for all other particles.
 The conservation of baryon number requires the same total baryon number
before and after the reaction.
 Although there are no known violations of baryon conservation, there are
theoretical indications that it was violated sometime in the beginning of the
universe when temperatures were quite high. This is thought to account for
the dominance of matter over antimatter in the universe today.

61. 61
Lepton Conservation
 The leptons are all fundamental particles, and there is a conservation of
leptons for each of the three kinds (families) of leptons.
 The number of leptons from each family is the same both before and
after a reaction.
 We let 𝐿𝑒 = +1 for the electron and the electron neutrino; 𝐿𝑒 = −1 for
their antiparticles; and 𝐿𝑒 = 0 for all other particles.
 We assign the quantum numbers 𝐿𝜇 for the muon and its neutrino and
𝐿𝜏 for the tau and its neutrino similarly.
 Thus three additional conservation laws are added.

62. 62
Strangeness
 In the early 1950s physicists had considerable difficulty understanding
the numerous observed reactions and decays. For example, the behavior
of the K mesons seemed very odd.
 There is no conservation law for the production of mesons, but it
appeared that K mesons, as well as the Λ and Σ baryons, were always
produced in pairs in the proton reaction studied most often, namely the
𝑝 + 𝑝 reaction.
 In addition, the very fast decay of the π0 meson into two photons (10−16
s) is the preferred mode of decay.
 One would expect the K0 meson to also decay into two photons very
quickly, but it does not. The long and short decay lifetimes of the K0 are
10−8 and 10−10 s, respectively.

63. 63
The New Quantum Number: Strangeness
 Strangeness, S, is conserved in the strong and
electromagnetic interactions, but not in the weak
interaction.
 The kaons have 𝑆 = +1, lambda and sigmas have
𝑆 = −1, the xi has 𝑆 = −2, and the omega has 𝑆 =
−3.
 When the strange particles are produced by the 𝑝 +
𝑝 strong interaction, they must be produced in pairs
to conserve strangeness.

64. 64
Contd…
 π0 can decay into two photons by the strong interaction, it is not
possible for K0 to decay at all by the strong interaction. The K0 is
the lightest 𝑆 = 0 particle, and there is no other strange particle
to which it can decay. It can decay only by the weak interaction,
which violates strangeness conservation.
 Because the typical decay times of the weak interaction are on
the order of 10−10 s, this explains the longer decay time for K0.
 Only Δ𝑆 = ±1 violations are allowed by the weak interaction.

65. 65
Hypercharge
 One more quantity, called hypercharge, has also become widely used as a
quantum number.
 The hypercharge quantum number 𝑌 is defined by 𝑌 = 𝑆 + 𝐵.
 Hypercharge, the sum of the strangeness and baryon quantum numbers,
is conserved in strong interactions.
 The hypercharge and strangeness conservation laws hold for the strong
and electromagnetic interactions, but are violated for the weak
interaction.

66. 66
Symmetries
 Symmetries lead directly to conservation laws.
 Three symmetry operators called parity, charge conjugation, and
time reversal are considered.

67. Quantum Electrodynamics
 In particle physics, quantum electrodynamics (QED) is
the relativistic quantum field theory of electrodynamics.
 It describes how light and matter interact and is the first theory
where full agreement between quantum mechanics and special
relativity is achieved.
 QED mathematically describes all phenomena involving electrically
charged particles interacting by means of exchange of photons and
represents the quantum counterpart of classical electromagnetism
giving a complete account of matter and light interaction.

68.  In other words, QED can be described as a perturbation theory of
the electromagnetic quantum vacuum.
 Richard Feynman called it "the jewel of physics" for its extremely
accurate predictions of quantities like the anomalous magnetic
moment of the electron and the Lamb shift of the energy
levels of hydrogen.

69. Electromagnetic force
e- e-
Photon
The repulsive force that two approaching electrons “feel”
Photon is the particle
associated to the electromagnetic force
“smallest bundle” of force

70. Photon exchange
Feynman Diagram
e- e-
e-
e-
g

71.  Here, two electrons enter, a photon
passes between them and the two then
exit. This diagram, then, describes the
interaction between two electrons
 In the classical theory it is the
Coulomb repulsion of like charges (if
the two are at rest).
 In QED this process is called Moller
scattering
 In QED, the interaction is “mediated by
the exchange of a photon,”
Time

72.  One can twist these
“Feynman diagrams”
around into any
topological
configuration .
Time

73.  As per the convention, a particle line running “backward in
time” (as indicated by the arrow) is to be interpreted as the
corresponding antiparticle going forward (the photon is its
own antiparticle.
 In this process an electron and a positron annihilate to form a
photon, which in turn produces a new electron-positron pair.
 An electron and a positron went in, an electron and a positron
came out
 This represents the interaction of two opposite charges: their
Coulomb attraction.
 In QED this process is called Bhabha scattering.

74.  Pair annihilation