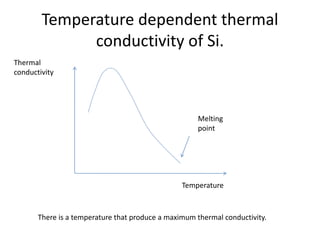
This document discusses lattice vibrations in solids. It begins by introducing different types of elementary excitations in solids including phonons, which are quantized elastic waves in a crystal. It then describes lattice vibrations as waves that propagate through the crystal as planes of atoms moving in and out of phase. Both longitudinal and transverse polarization of these waves are discussed. Equations of motion are provided and solved to show the wave-like behavior of lattice vibrations. The document also covers phonon dispersion relations, group velocity, Brillouin zones, phonons in diatomic crystals, quantization of elastic waves, phonon momentum, heat capacity of lattices, and early models like Einstein and Debye models to explain temperature-dependent

1. UEEP2024 Solid State Physics
Topic 2 Crystal dynamics

2. Important elementary excitation in
solids
Name Field
Electron -
Photon Electromagnetic wave
Phonon Elastic wave
Plasmon Collective electron wave
Magnon Magnetic wave
Polaron Electron +elastic deformation
Exciton Polarization wave

3. Lattice Vibration
• In a real crystal at a finite temperature T, the basis of each
lattice point and indeed also the constituent atoms of each
basis vibrate relative to the fixed lattice and with each other.
As the atoms or ions are physically linked together through
the bonding system, the vibrational motion is in general not
isolated.
• When a wave propagate along the crystal, entire planes of
atoms move in phase with displacement either parallel or
perpendicular to the direction of wavevector.

4. Longitudinal polarization
Dashed line –Planes of atoms when in equilibrium.
Solid lines- Planes of atoms when displaced.
Coordinate u measures the displacement of the planes

5. Transverse wave
• Planes of atom as displaced during passage of a
transverse wave.

6. Lattice Vibration
  
p
spsps uucf )(
where cp is the force constant for the neighbour p. Let m be the mass of one
atom. The equation of motion is given by
For a 1-D long chain with discrete atoms of equilibrium separation a , Let us be
the displacement of the reference atom labelled by s. We assume that the net
force exerted on atom s is due to its different neighbours labelled p. Now the
total force on atom s is obtained by summing the forces from all its possible
neighbours p on both sides. Hence
  
p
spsps uucdtumd )(/ 22
(1)
(2)

7. Lattice Vibration
The wave-like solution is
)](exp[)( tqxiAxu  (3)
ω is the angular frequency
q is the wavevector
P = h/2 x q
E = h/2 x ω
The vibrational motion in the crystal is regarded as a kind of wave
propagation. Because of the finite extent of the crystal, the wave motion is
often regarded as a standing wave system. the phonon is defined to be
the quantised energy of elastic waves in a crystal. The phonons are similar
to the photons in electromagnetic waves in many respects. Both of these
two excitations exhibit the duality property, namely possessing both wave-
like and particle-like behaviour.

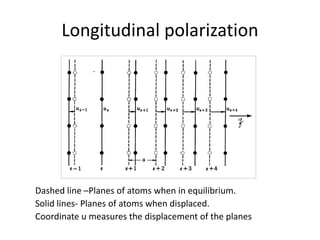
8. Lattice Vibration
Remember that we are dealing with discrete atoms of equilibrium
separation a. Thus for any general atoms with label s + p, x should be
replaced by (s + p)a.
)exp(])(exp[ tiqapsiuu ps  (4)
Substituting this solution (4) in the equation of motion, we obtain
]1)[exp(2
  ipqacm pp (5)
for the lattice with inversion symmetry about the origin, (5) may be
re-written as
)]cos(1[)/2(2
pqacm pp   (6)

9. Lattice Vibration
Eq(6) is the dispersion relation for phonons
the mathematical expression of energy (frequency) in terms of the wavevector
if we simplify (6) by considering only nearest neighbours (p=1), we get
)2/sin()/4( 2
1
1 aqmc (7)

10. Group Velocity of Phonons
(3) –(7) show the wave nature of lattice vibration. The group velocity is
then given by the derivative of (7)
)2/cos()/(/ 2
1
2
1 qamacdqdv  
For long wavelength
V ≈ a(c1/m)0.5
For short wavelength
V ≈ 0

11. The Brillouin zone
considering the waves in figure below
The wave represented by the solid curve conveys no information not given by
the dashed curve. Only wavelengths longer than 2a are needed to represent
the motion. Essentially, what it implies is that if the wavevector is larger than
/a, you can always find a smaller wavevector q < /a which is just as a good
representation. So this means that in a solid, there is a maximum limit for the
wavevector and in 1 D this is /a.
aqa //  

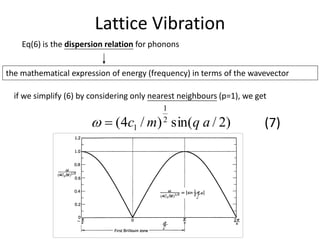
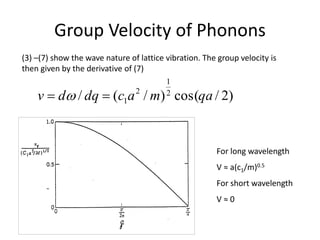
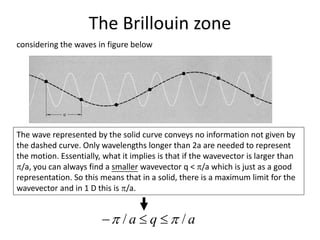
12. The Brillouin zone
“if the wavevector is larger than /a, you can always find a smaller
wavevector q < /a which is just as a good representation”
How ??
Consider two wavevector q and q + n(2π/a) where n is an integer
)exp()2exp()exp(
])/2(exp[
iqaniiqa
aanqi




)/2(' anqq 
 q outside the first zone
q' the corresponding value inside the zone

13. Photons in Diatomic Crystals
When the primitive basis of a crystal contains more than one atom, e.g. NaCl and
diamond structure, the phonon dispersion relation has more than one branch.
The figure shows the acoustical and optical branches of only one polarisation

14. Photons in Diatomic Crystals
• For both the acoustical and the optical frequency
ranges there should be two transverse and one
longitudinal polarisations.
• For a diatomic crystal, there are three optical
branches (one longitudinal LO and two transverse TO)
and three acoustical branches (one longitudinal LA
and two transverse TA).
• For a general basis with p atoms, there are three
acoustical branches and (3p - 3) optical branches.

15. Photons in Diatomic Crystals
Experimental dispersion curves for diamond in the (100) and (111)
directions, where q is the reduced wavevector in units of /a

16. Quantization of Elastic Waves
• The energy of a lattice vibration is quantized.
• The quantum of energy is called a phonon in
analogy with the photon of the
electromagnetic wave.
• The energy of an elastic mode of angular
frequency w is E = (n + ½) ħw when the mode
is excited to quantum number n.
• The term ½ ħw is the zero energy of the mode.

17. Phonon Momentum
• A phonon of wavevector q will interact with particles such
as photons, neutrons and electrons as if it had a
momentum ħq.
• Phonon does not carry physical momentum.
• In crystal there exist wavevector selection rules for allowed
transitions between quantum states.
• In elastic scattering of a crystal is governed by the
wavevector selection rule K’ = K +G, where G is a vector in
the reciprocal lattice, K is the wavevector of the incident
photon and K’ is the wavevector of the scattered photon.
• If scattering is inelastic, with the creation of phonon of
wavevector q, then the selection rule is K’+q = K +G.
• If a phonon q is absorbed in the process, K’ =q + K +G.

18. Inelastic scattering by phonons
• One way to determine the dispersion relation
of phonons in a solid is to use the technique
of inelastic neutron scattering.

19. Inelastic scattering by phonons
• elastic
– the energy of the incident particles is conserved,
only their direction of propagation is modified.
• Inelastic
– the energy of the incident particle is not
conserved. In this scattering process, the energy
of the incident particle is lost or gained.

20. Inelastic scattering by phonons
• The laws of Physics used for the measurement are the
energy and momentum conservation laws for the neutrons
and the phonons involved
• the i and f subscripts denote the initial and final values for
the neutron before and after scattering by a phonon in the
crystal, the  are the angular frequencies, q is the
wavevector of the phonon
• In the experiment, the incoming neutron source has a well
defined energy and direction. Thus the initial frequency
and wavevector of the neutron before scattering are
precisely known.
qkk fi
pfi

 

21. Heat capacity
U is energy and T the temperature
T
U
C



CV – heat capacity at constant volume
CP – heat capacity at constant pressure
Clat – lattice heat capacity

22. Heat Capacity of the lattice
• Classical statistical mechanics explained the
heat capacity of insulators at room
temperature fairly well but failed for lower
temperatures and it totally failed for metals.
• Metals were expected to have much higher
heat capacity than insulators because of of
many free electrons but it turn out that a
metal’s heat capacity at room temperature is
similar to that of insulator.

23. Classical theory and experimental
results
• Classical statistical mechanics, gives a numerical
value for the heat capacity of a solid.
• One dimensional harmonic oscillator, the mean
energy is KT.
• Three dimensional harmonic oscillator, the mean
energy is 3KT.
• The heat capacity must be 3K and for 1 mole is 3R
= 24.9 J K-1, independent of temperature.
• This is the rule of Dulong-Petit.
• Good at room temperature.

24. Molar heat capacity (JK-1) of different solids at
liquid nitrogen temperature and room
temperature.
Material 77K 273K
Cu 12.5 24.3
Al 9.1 23.8
Au 19.1 25.2
Pb 23.6 26.7
Fe 8.1 24.8
Diamond 0.1 5.2

25. Classical theory and experimental
results
• Classical statistical mechanics, predict a
temperature independent heat capacity
whereas the heat capacity has to vanish at
zero temperature.
• A vanishing heat capacity at zero temperature
is support by experimental results.
• The low-temperature dependence suggesting
a power law behavior, C  T3.

26. Einstein Model
• Einstein model explain the temperature-
dependent heat capacity of solids.
• Einstein solve the problem using quantum
theory to describe the oscillators in the solid.
• It starts out by assuming that the solid’s
vibration are represented by independent
harmonic oscillators that all have same
frequency, the Einstein frequency ωE, so that
their energy levels are
En nE 






2
1

27. Einstein Model
• The mean energy for 3Na of these oscillators
per mole of atoms is
• The mean quantum number <n> can be found
using Bose-Einstein distribution since lattice
vibrations are bosonic character,
• The resulting mean energy for 3NA oscillators
is
.
2
1
3 EA nNE 






.
1
1


KT
E
e
n 
E
KT
A E
e
NE 
 










2
1
1
1
3

28. Einstein Model
• The heat capacity is found by differentiation:
• At high temperature, Einstein model correctly
reproduces the Dulong-Petit value.
• High temperature means that temperature
must be as high as the Einstein temperature
2
2
1
33
























KT
KT
E
V
A
E
E
e
e
KT
R
T
E
NC






.
K
E
E



29. Einstein Model
• The heat capacity drops to zero at absolute
zero temperature.
• At low temperature, it shows exponential
behavior whereas the experimental shows a
power law behavior C  T3.

30. Debye Model
• Use a more realistic model for the lattice
vibration at low energies.
• The excitations with the lowest energies near
k =0 are those with the longest wavelength
corresponds to sound waves with ω(k) = vk.
• For low temperature, the Debye assumption is
appropriate and it leads to good results.

31. Heat capacity

q p
pqpqnU ,, 
The total energy of the phonons in a crystal
<n> is the thermal equilibrium occupancy of
phonons
1)exp(
1


kT
n

(1)
(2)

32. Heat capacity



q p pq
pq
kT
U
1)exp( ,
,




From (1) and (2), we have
(3)
Suppose that the crystal has Da()d modes of a
given polarization a in the frequency range  to
+d




a
a d
kT
DU
pq
pq
1)/exp(
)(
,
,

  

(4)

33. Heat capacity


d
dN
D )(
Density of states
(The number of modes per
unit frequency range)
lattice heat capacity





a
a d
kT
kT
kT
Dk
T
U
C
pq
pq
pq
lat
2
,
,
2
,
]1)/[exp(
)/exp(
)(











 



34. Density of states
L
s = 0 s = M+1
Consider a 1-D line of length L carrying M+1 particles at
separation “a”
Boundary condition – the particles at the ends of the line are
held fixed
us, the displacement of the particle s
)sin()exp()0( sqatiuus 

35. Density of states
L
M
LLLL
q
 )1(
,......,
4
,
3
,
2
,


 


 d
dqL
d
dN
D
Lq
N 
The wavevector q
There are M-1 allowed independent value of q, thus
0 /L 2/L
K-space
q

36. Density of states
)()( Lsausau 
L
M
LLLL
q

,......,
8
,
6
,
4
,
2
,0 
0 2/L 4/L
K-space
q
2/L
For periodic boundary conditions
 


d
dqL
D 
One allowed value of q per 2/L

37. Density of states (in 3-D)
• 3-D system
• periodic boundary conditions
L
M
LLLL
qqq zyx

,......,
8
,
6
,
4
,
2
,0,, 
One allowed value of q per volume (2/L)3
Thus
 



 d
dqqL
D
qL
N 

















 2
2333
23
4
2

38. Debye Model
• Debye frequency ωD, where
• Debye temperature
• Use Debye model the heat capacity of the
solid can be determined.
• At high temperature, the resulting energy
• For 1 mole of atoms, this is equal to 3RT,
leads to the Dulong-Petit result.
.6 323
v
V
N
D  
.
B
D
D k
h 
.2 TNKE B

39. Debye Model
• At low temperature, the heat capacity
• This is the Debye T3 law, that fits the
experimental data far better than the
exponential behavior of Einstein model.
.
5
12
34







D
B
T
NkC



40. Harmonic theory
• Two lattice wave do not interact
• No thermal expansion
• Adiabatic and isothermal elastic
constants are equal
• The elastic constants are
independent of pressure and
temperature
In real crystals, none of the consequences is
satisfied accurately
Neglect the
anharmonic
effect

41. Thermal Conductivity
• Transport of heat through a crystal by lattice vibrations.
• Metals usually have much better thermal conductivity
than insulators.
• Contribution of the electrons to thermal conductivity is
generally more important than the lattice contribution.
• However this is not always the case, example is the
insulator diamond that has one of the highest thermal
conductivities of all materials at room temperature.
• The total thermal conductivity is the sum of the lattice
and electron thermal conductivity.

42. Thermal Conductivity
dx
dT
KjU 
jU is the flux of thermal energy, or the energy transmitted across
unit area per unit time
CvLK
3
1

Thermal conductivity
C – heat capacity per unit volume
v – average velocity
L – mean free path

43. Thermal Conductivity
• The phonon mean free path is determined by two
process
– Geometrical scattering (dominate
at low T) (scattering by imperfection in lattice,
such as point defects, dislocation etc)
– Scattering by other phonon (dominate
at high T)
T
L
1

specimenofdiameterDL ,
(high T)
(low T)

44. Thermal Conductivity at low
temperature
• At low temperature, heat capacity decrease
and causing thermal conductivity to decease.
• At low temperature, as phonons propagated
through the crystal, they can be scattered by
imperfection in the lattice, such as point
defects, dislocations and the like.
• It is possible to grow crystal of such high
perfection that scattering effects become
unimportant.
• The scattering of phonon at the sample
boundary can be observed experimentally.

45. Thermal Conductivity at high
temperature
• At high temperature another scattering
process become dominant.
• The number of phonon increases and
phonon can be scattered from other
phonons.
• This causes the mean free path to decrease.
• Thermal conductivity decreases with
temperature.

46. Thermal conductivity K for metals and
insulators at room temperature
Material K(W m-1 K-1)
Copper 386
Aluminium 237
Steel 50
Diamond 2300
Quartz 10
Glass 0.8
Polystyrene 0.03

47. Temperature dependent thermal
conductivity of Si.
Temperature
Thermal
conductivity
Melting
point
There is a temperature that produce a maximum thermal conductivity.