Download as PDF, PPTX
Uploaded byMandava Ramya
(3) heat conduction equation [compatibility mode]
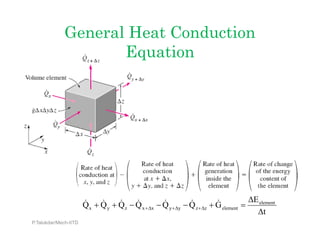
The document discusses heat conduction equations in various coordinate systems and geometries: 1) It presents Fourier's law of heat conduction and derives the one-dimensional heat conduction equation. 2) It then extends the derivation to multidimensional systems, deriving equations for cylindrical and spherical geometries with variable or constant conductivity. 3) Finally, it presents the general three-dimensional heat conduction equation applicable to problems involving transient or steady heat transfer in solids with arbitrary geometries and material properties.
More Related Content
Similar to (3) heat conduction equation [compatibility mode]
(3) heat conduction equation [compatibility mode]
- 1. HEAT CONDUCTION EQUATION PrabalTalukdarPrabal Talukdar Associate Professor Department of Mechanical EngineeringDepartment of Mechanical Engineering IIT Delhi E-mail: prabal@mech.iitd.ac.inp
- 2. Heat TransferHeat Transfer Heattransfer has direction as well as magnitude, and thus it is a vector quantity P.Talukdar/Mech-IITD
- 3. Coordinate SystemCoordinate System Thevarious distances and angles involved when describing the location of a point in different coordinate systems P.Talukdar/Mech-IITD location of a point in different coordinate systems.
- 4. Fourier’s law ofheat conduction for one-dimensional heat conduction: )Watt( dx dT kAQcond −=& If n is the normal of the isothermal surface at point P, the rate of heat conduction at that point can be expressed by Fourier’s law as The heat transfer vector is )Watt( n T kAQn ∂ ∂ −=& always normal to an isothermal surface and can be resolved into its components like any other vectorother vector kQjQiQQ zyxn r & r & r & r & ++= P.Talukdar/Mech-IITD x T kAQ xx ∂ ∂ −=& y T kAQ yy ∂ ∂ −=& z T kAQ zz ∂ ∂ −=&
- 5. Steady versus TransientHeat Transfer • The term steady implies noy p change with time at any point within the medium, while transient implies variationtransient implies variation with time or time dependence. Therefore, the temperature or heat flux remains unchanged with time during steady heat transfer through a medium atg any location, although both quantities may vary from one location to anotherlocation to another P.Talukdar/Mech-IITD
- 6. Multidimensional Heat Transfer • Heattransfer problems are also classified as being one-p g dimensional, two-dimensional, or three-dimensional, depending on the relative magnitudes of heat transfer rates in different directions and the level of accuracy desireddifferent directions and the level of accuracy desired Ex: 1‐D heat transfer: Heat transfer through the glass of a i d b id d t bwindow can be considered to be one‐ dimensional since heat transfer through the glass will occur predominantly in one direction (the direction normal to the ( surface of the glass) and heat transfer in other directions (from one side edge to the other and from the top edge to the bottom) is negligible P.Talukdar/Mech-IITD to the bottom) is negligible
- 7. Heat GenerationHeat Generation •A medium through which heat is conducted may involve the conversion of electrical nuclear or chemical energy into heatconversion of electrical, nuclear, or chemical energy into heat (or thermal) energy. In heat conduction analysis, such conversion processes are characterized as heat generation. • Heat generation is a volumetric phenomenon. That is, it occurs throughout the body of a medium. Therefore, the rate of heat generation in a medium is usually specified per unit volumegeneration in a medium is usually specified per unit volume whose unit is W/m3 The rate of heat generation in a medium may vary with time as wellmedium may vary with time as well as position within the medium. When the variation of heat generation with position is known, ∫= V dVgG && Watt P.Talukdar/Mech-IITD g p the total rate of heat generation in a medium of volume V can be determined from V
- 8. 1-D Heat ConductionEquationq Assume the density of the wall is ρ, the specific heat is C, and the area of the wall normal to the direction of heat transfer is A. An energy balance on this thin element during a small time interval t can be expressed asa small time interval t can be expressed as EΔ P.Talukdar/Mech-IITD t E GQQ element elementxxx Δ Δ =+− Δ+ &&&
- 9. )TT(x.A.C)TT(mCEEE tttttttttelement −Δρ=−=−=ΔΔ+Δ+Δ+ x.A.gVgG elementelement Δ== &&& E GQQ elementΔ + &&& t GQQ element elementxxx Δ =+− Δ+ )TT( ACAQQ ttt − ΔΔ Δ+ &&& Dividing by t )( x.A.Cx.A.gQQ ttt xxx Δ Δρ=Δ+− Δ+ Δ+ & TTQQ1 −− &&g y AΔx gives t TT Cg x QQ A 1 tttxxx Δ ρ=+ Δ − Δ+Δ+ & Taking the limit as Δx → 0 and Δt → 0 yields and since from Fourier’s Law: ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ − ∂ ∂ = ∂ ∂ = Δ −Δ+ →Δ x T kA xx Q x QQ xxx 0x lim &&& TT1 ∂⎞⎛ ∂∂ P.Talukdar/Mech-IITD ⎠⎝→Δ 0x t T Cg x T kA xA 1 ∂ ∂ ρ=+⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ &
- 10. Plane wall: Ais constant TT ∂⎞⎛ ∂∂ Variable conductivity: t T Cg x T k x ∂ ∂ ρ=+⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ & T1gT2 ∂∂ & Constant conductivity: where the property k/ρC is the thermal t T1 k g x T 2 ∂ ∂ α =+ ∂ ∂ diffusivity P.Talukdar/Mech-IITD
- 11. Heat Conduction Equationin a L C li d C id thi li d i l h ll l t f Long Cylinder Consider a thin cylindrical shell element of thickness r in a long cylinder The area of the cylinder normal to they direction of heat transfer at any location is A = 2πrL where r is the value of the radius at that location. Note that the heat transfer area A depends on r in this case and thus it varies withdepends on r in this case, and thus it varies with location. E lΔ&&& P.Talukdar/Mech-IITD t E GQQ element elementrrr Δ Δ =+− Δ+
- 12. )TT(r.A.C)TT(mCEEE tttttttttelement −Δρ=−=−=ΔΔ+Δ+Δ+ r.A.gVgG elementelement Δ== &&& )TT( −&& t )TT( r.A.Cr.A.gQQ ttt rrr Δ Δρ=Δ+− Δ+ Δ+ &&& TTQQ1 && dividing by AΔr gives t TT Cg r QQ A 1 tttrrr Δ − ρ=+ Δ − − Δ+Δ+ & ⎟ ⎞ ⎜ ⎛ ∂∂∂−Δ+ T kA QQQ li &&& ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ − ∂ ∂ = ∂ ∂ = Δ Δ+ →Δ r T kA rr Q r QQ rrr 0r lim T C T kA 1 ∂ +⎟ ⎞ ⎜ ⎛ ∂∂ & P.Talukdar/Mech-IITD t Cg r kA rA ∂ ρ=+⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂∂
- 13. Different ExpressionsDifferent Expressions Variableconductivity: T Cg T kr 1 ∂ ρ+⎟ ⎞ ⎜ ⎛ ∂∂ &Variable conductivity: t Cg r .k.r rr ∂ ρ=+⎟ ⎠ ⎜ ⎝ ∂∂ T1gT1 ∂ ⎟ ⎞ ⎜ ⎛ ∂∂ & Constant Conductivity: t T1 k g r T r rr 1 ∂ ∂ α =+⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ 0 gdTd1 ⎟ ⎞ ⎜ ⎛ & 0 k g rd r drr =+⎟ ⎠ ⎞ ⎜ ⎝ ⎛ t T1 r T r rr 1 ∂ ∂ α =⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ trrr ∂α⎠⎝ ∂∂ 0 rd dT r dr d =⎟ ⎠ ⎞ ⎜ ⎝ ⎛ P.Talukdar/Mech-IITD
- 14. Heat Conduction Eqin a SphereHeat Conduction Eq. in a Sphere A = 4πr2 Variable conductivity: t T Cg r T .k.r rr 1 2 2 ∂ ∂ ρ=+⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ & Constant Conductivity: t T1 k g r T r rr 1 2 2 ∂ ∂ α =+⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ & P.Talukdar/Mech-IITD Combined One‐Dimensional Heat Conduction Equation t T Cg r T .k.r rr 1 n n ∂ ∂ ρ=+⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ &
- 15. General Heat Conduction EiEquation E lΔ&&&&&&& P.Talukdar/Mech-IITD t E GQQQQQQ element elementzzyyxxzyx Δ Δ =+−−−++ Δ+Δ+Δ+
- 16. )TT.(z.y.x.C)TT(mCEEE tttttttttelement −ΔΔΔρ=−=−=ΔΔ+Δ+Δ+ z.y.x.gVgG elementelement ΔΔΔ== &&& t E GQQQQQQ element elementzzyyxxzyx Δ Δ =+−−−++ Δ+Δ+Δ+ &&&&&&& t TT z.y.x.Cz.y.x.gQQQQQQ ttt zzyyxxzyx Δ − ΔΔΔρ=ΔΔΔ+−−−++ Δ+ Δ+Δ+Δ+ &&&&&&& TT Cg QQ1QQ1QQ1 tttzzzyyyxxx − ρ=+ −−− Δ+Δ+Δ+Δ+ & &&&&&& t Cg zy.xyz.xxz.y Δ ρ=+ ΔΔΔ − ΔΔΔ − ΔΔΔ − P.Talukdar/Mech-IITD
- 17. TT C QQ1QQ1QQ1 tttzzzyyyxxx −−−−Δ+Δ+Δ+Δ+ & &&&&&& t Cg z QQ y.xyz.xx QQ z.y tttzzzyyyxxx Δ ρ=+ ΔΔΔ − ΔΔΔ − ΔΔΔ − Δ+Δ+Δ+Δ+ ⎞⎛ ∂∂⎞⎛ ∂∂∂ TT1Q1QQ1 &&& ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ − ∂ ∂ =⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ΔΔ− ∂ ∂ ΔΔ = ∂ ∂ ΔΔ = Δ − ΔΔ Δ+ →Δ x T k xx T z.y.k xz.y 1 x Q z.y 1 x QQ z.y 1 lim xxxx 0x ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ − ∂ ∂ =⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ ΔΔ− ∂ ∂ ΔΔ = ∂ ∂ ΔΔ = Δ − ΔΔ Δ+ →Δ y T k yy T z.x.k yzx 1 y Q zx 1 y QQ zx 1 lim yyyy 0y &&& ⎠⎝ ∂∂⎠⎝ ∂∂ΔΔ∂ΔΔΔΔΔ→Δ yyyyz.xyz.xyz.x0y ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ − ∂ ∂ =⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ΔΔ− ∂ ∂ ΔΔ = ∂ ∂ ΔΔ = Δ − ΔΔ Δ+ →Δ z T k zz T y.x.k zy.x 1 z Q y.x 1 z QQ y.x 1 lim zzzz 0z &&& t T Cg z T k zy T k yx T k x ∂ ∂ ρ=+⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ +⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ +⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ & Under what condition? T1gTTT 222 ∂∂∂∂ & P.Talukdar/Mech-IITD t T1 k g z T y T x T 222 ∂ ∂ α =+ ∂ ∂ + ∂ ∂ + ∂ ∂
- 18. 0 k gTTT 2 2 2 2 2 2 =+ ∂ ∂ + ∂ ∂ + ∂ ∂ & kzyx 222 ∂∂∂ t T1 z T y T x T 2 2 2 2 2 2 ∂ ∂ α = ∂ ∂ + ∂ ∂ + ∂ ∂ tzyx∂α∂∂∂ 0 z T y T x T 2 2 2 2 2 2 = ∂ ∂ + ∂ ∂ + ∂ ∂ y P.Talukdar/Mech-IITD
- 19. Cylindrical and SphericalCylindricaland Spherical T Cg T k T rk 1T rk 1 ∂ ρ=+⎟ ⎞ ⎜ ⎛ ∂∂ +⎟⎟ ⎞ ⎜⎜ ⎛ ∂∂ +⎟ ⎞ ⎜ ⎛ ∂∂ & t Cg z .k z r.k rr r.k rr 2 ∂ ρ=+⎟ ⎠ ⎜ ⎝ ∂∂ +⎟⎟ ⎠ ⎜⎜ ⎝ φ∂φ∂ +⎟ ⎠ ⎜ ⎝ ∂∂ T Cg T sink 1T k 1T rk 1 2 ∂ ρ=+⎟ ⎞ ⎜ ⎛ ∂ θ ∂ +⎟⎟ ⎞ ⎜⎜ ⎛ ∂∂ +⎟ ⎞ ⎜ ⎛ ∂∂ & P.Talukdar/Mech-IITD t Cgsin.k sinr k sinrr r.k rr 2222 ∂ ρ=+⎟ ⎠ ⎜ ⎝ θ∂ θ θ∂θ +⎟⎟ ⎠ ⎜⎜ ⎝ φ∂φ∂θ +⎟ ⎠ ⎜ ⎝ ∂∂
- 20. Boundary and InitialConditions • The temperature distribution in a medium depends on the conditions at the boundaries of the medium as well as the heat transfer mechanism inside the medium. To describe a heat transfer problem completely, two boundary conditions must be given for each direction of the coordinate system along whichgiven for each direction of the coordinate system along which heat transfer is significant. Th f d ifTherefore, we need to specify two boundary conditions for one-dimensional problems, four boundary conditions for two dimensional problems and sixtwo-dimensional problems, and six boundary conditions for three-dimensional problems P.Talukdar/Mech-IITD
- 21. • A ditihi h i ll ifi d t ti t 0 i ll d• A condition, which is usually specified at time t = 0, is called the initial condition, which is a mathematical expression for the temperature distribution of the medium initially. )z,y,x(f)0,z,y,x(T = • Note that under steady conditions, the heat conduction equation does not involve any time derivatives, and thus we do not need to specify an initial conditionp y The heat conduction equation is first order in time, and thus the initial condition cannot involve any derivatives (it is limited to a specified temperature). However, the heat conduction equation is second order in space coordinates, and thus a boundary condition may involve first d i ti t th b d i ll ifi d l f t t P.Talukdar/Mech-IITD derivatives at the boundaries as well as specified values of temperature
- 22. Specified Temperature Boundary Cdi iCondition The temperature of an exposed surface can usually be measured directly and easily. Therefore, one of the easiest ways toy specify the thermal conditions on a surface is to specify the temperature. For one- dimensional heat transfer through a plane wall of thickness L, for example, the specified temperature boundary conditions can be expressed as 1T)t,0(T = 2T)t,L(T = P.Talukdar/Mech-IITD 2)(
- 23. Specified Heat FluxBoundary C di iCondition The sign of the specified heat flux isThe sign of the specified heat flux is determined by inspection: positive if the heat flux is in the positive direction of the coordinate a is anddirection of the coordinate axis, and negative if it is in the opposite direction. Note that it is extremely important to have the correct sign for the specifiedhave the correct sign for the specified heat flux since the wrong sign will invert the direction of heat transfer and cause the heat gain to be P.Talukdar/Mech-IITD and cause the heat gain to be interpreted as heat loss
- 24. For a plateof thickness L subjected to heat flux of 50 W/m2 into theFor a plate of thickness L subjected to heat flux of 50 W/m into the medium from both sides, for example, the specified heat flux boundary conditions can be expressed as 50 x )t,0(T k = ∂ ∂ − 50 x )t,L(T k −= ∂ ∂ −and Special Case: Insulated Boundary 0 x )t,0(T k = ∂ ∂ 0 x )t,0(T = ∂ ∂or P.Talukdar/Mech-IITD
- 25. Another Special CaseAnotherSpecial Case • Thermal SymmetryThermal Symmetry t, 2 L T ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ 0 x 2 = ∂ ⎠⎝ PTalukdar/Mech-IITD
- 26.
- 27.
- 28.