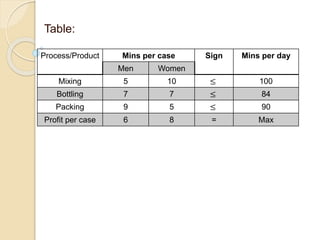
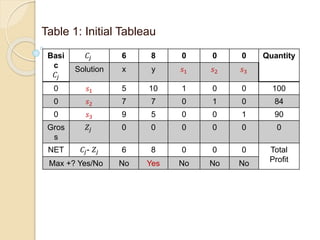
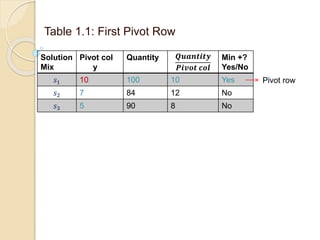
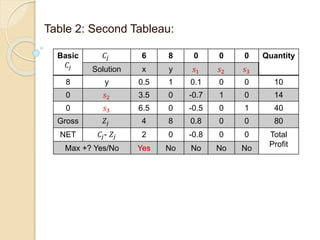
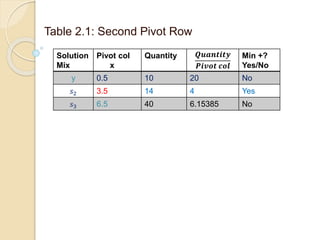
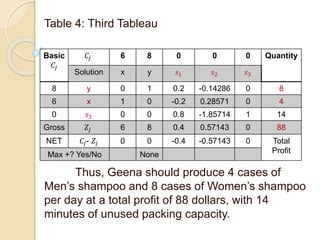
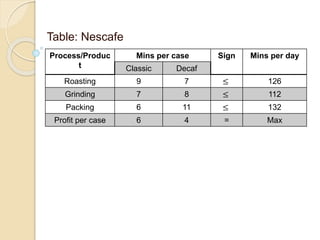
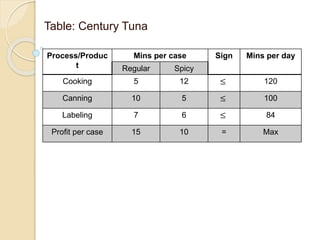
The document describes an example of using the simplex method to solve a linear programming problem (LPP) for determining the optimal production mix of two products. Specifically, it involves determining the number of cases of men's and women's shampoo a company should produce daily to maximize profits given constraints on available minutes for mixing, bottling, and packing. The simplex method is applied through four steps, arriving at a solution of producing 4 cases of men's shampoo and 8 cases of women's shampoo daily for a total profit of $88 and 14 minutes of unused packing capacity. A second similar example involving classic and decaf coffee production at Nescafe is also presented.

1. Solving LPP by Simplex
Method

2. Example 1: Clear Shampoo
Geena is the Production Manager of Clear Shampoo
and she wants to determine the production mix that will
result in maximum profit. She is able to determine the data
necessary for her to make a decision. It will take 5 minutes
to mix 1 case of Men’s shampoo and 10 minutes to mix 1
case of Women’s shampoo and she has a total of 100 mins
available for the mixing process per day. It will take 7
minutes to bottle 1 case of Men’s shampoo and 7 minutes to
bottle 1 case of Women’s shampoo and she has a total of
84 mins available for the bottling process per day. It will take
9 minutes to pack 1 case of Men’s shampoo and 5 minutes
to pack 1 case of Women’s shampoo and she has a total of
90 mins available for the packing process per day. She will
earn 6 dollars for every case of Men’s shampoo produced
and 8 dollars for every case of Women’s shampoo
produced.
How many cases of Men’s shampoo and Women’s
shampoo should be produced per day to maximize profits?
How much is the total profit?

3. Table:
Process/Product Mins per case Sign Mins per day
Men Women
Mixing 5 10 ≤ 100
Bottling 7 7 ≤ 84
Packing 9 5 ≤ 90
Profit per case 6 8 = Max

4. Solution:
STEP 1: Develop the initial tableau (Table 1).
1. Set up the variables.
x = number of cases of Men’s shampoo to be
produced
per day
y = number of cases of Women’s shampoo to be
produced per day
𝑠1= slack 1 or unused minutes of constraint A
(mixing)
𝑠2= slack 2 or unused minutes of constraint B
(bottling)
𝑠 = slack 3 or unused minutes of constraint C

5. 2. Set up the objective function where 0 is the
assigned
profit per unit of a slack variable:
Maximize P = 6x + 8y + 0𝑠1 + 0𝑠2 + 0𝑠3

6. 3. Convert the constraints into equalities.
Constraint A (mixing)
5x + 10y ≤ 100
5x + 10y + 1𝑠1 + 0𝑠2 + 0𝑠3 = 100
Constraint B (bottling)
7x + 7y ≤ 84
7x+ 7y + 0𝑠1 + 2𝑠2 + 0𝑠3= 84
Constraint C (packing)
9x + 5y ≤ 90
9x + 5y + 0𝑠1 + 0𝑠2 + 3𝑠3= 90

7. 4. Compute the 𝑍𝑗 values:
𝑍𝑗 = sumproduct (basic 𝐶𝑗 column, variable
column)
0 = 0(5) +0(7) + 0(9)
0 = 0(10) + 0(7) + 0(5)
0 = 0(1) + 0(0) + 0(0)
0 = 0(0) + 0(1) + 0(0)
0 = 0(0) + 0(0) + 0(1)
0 = 0(100) + 0(84) + 0(90)
= 0 dollar of total profit for this solution

8. 5. Compute the (𝐶𝑗- 𝑍𝑗) values:
𝐶𝑗- 𝑍𝑗 = 𝐶𝑗 row − 𝑍𝑗 row
6 = 6 – 0
8 = 8 – 0
0 = 0 – 0
0 = 0 – 0
0 = 0 – 0

9. 6. Determine the maximum positive (𝐶𝑗- 𝑍𝑗) value:
8 = +maximum (6, 8, 0, 0, 0)
= pivot column is y

10. Table 1: Initial Tableau
Basi
c
𝐶𝑗
𝐶𝑗 6 8 0 0 0 Quantity
Solution x y 𝑠1 𝑠2 𝑠3
0 𝑠1 5 10 1 0 0 100
0 𝑠2 7 7 0 1 0 84
0 𝑠3 9 5 0 0 1 90
Gros
s
𝑍𝑗 0 0 0 0 0 0
NET 𝐶𝑗- 𝑍𝑗 6 8 0 0 0 Total
ProfitMax +? Yes/No No Yes No No No

11. STEP 2: Determine the pivot row
1. Compute the quantity ratio (𝑄 𝑟):
𝑄 𝑟= Q/pivot column
10 = 100/10
12 = 84/7
18 = 90/5
2. Determine the minimum positive quantity ratio
10 = +minimum (10, 12, 18)
= pivot row is 𝑠1
3. Determine the pivot number:
10 = intersection of pivot column and pivot row

12. Table 1.1: First Pivot Row
Solution
Mix
Pivot col
y
Quantity 𝑸𝒖𝒂𝒏𝒕𝒊𝒕𝒚
𝑷𝒊𝒗𝒐𝒕 𝒄𝒐𝒍
Min +?
Yes/No
𝑠1 10 100 10 Yes
𝑠2 7 84 12 No
𝑠3 5 90 8 No
Pivot row

13. STEP 3: Develop the second tableau (Table 2)
1. Replace the pivot row with the pivot column in
solution column:
Exit = 0𝑠1
Enter = 8 y
2. Replace the 𝑠1 row of the initial tableau with the
y
row in the second tableau:
y row = 𝑠1 row of the initial tableau/pivot
number
0.5 = 5/10 0 = 0/10
1 = 10/10 0 = 0/10

14. 3. Replace the 𝑠2 row of the initial tableau with
new
values in the second tableau:
New 𝑠2 row = old 𝑠2 row – (number in old 𝑠2 row
and pivot column)(y row)
3.5 = 7 – 7(0.5)
0 = 7 – 7(1.0)
-0.7 = 0 – 7(0.1)
1 = 1 – 7(0)
0 = 0 – 7(0)
14 = 84 – 7(10)

15. 4. Replace the 𝑠3 row of the initial tableau with
new
values in the second tableau:
New 𝑠3 row = old 𝑠3 row – (number in old 𝑠3 row
and pivot column)(y row)
6.5 = 9 – 5(0.5)
0 = 5 – 5(1.0)
-0.5 = 0 – 5(0.1)
0 = 0 – 5(0)
1 = 1 – 5(0)
40 = 90 – 5(10)

16. 5. Compute the 𝑍𝑗 values:
𝑍𝑗 = sumproduct (basic 𝐶𝑗 column, variable
column)
4 = 8(0.5) +0(3.5) + 0(6.5)
8 = 8(1) + 0(0) + 0(0)
0.8 = 8(0.1) + 0(-0.7) + 0(-0.5)
0 = 8(0) + 0(1) + 0(0)
0 = 8(0) + 0(0) + 0(1)
80 = 8(10) + 0(14) + 0(40)
= 80 dollar of total profit for this solution

17. 6. Compute the (𝐶𝑗- 𝑍𝑗) values:
𝐶𝑗- 𝑍𝑗 = 𝐶𝑗 row − 𝑍𝑗 row
2 = 6 – 4
0 = 8 – 8
-0.8 = 0 – 0.8
0 = 0 – 0
0 = 0 – 0

18. 7. Determine the maximum positive (𝐶𝑗- 𝑍𝑗) value:
2 = +maximum (2, 0, -0.8, 0, 0)
= pivot column is x

19. Table 2: Second Tableau:
Basic
𝐶𝑗
𝐶𝑗 6 8 0 0 0 Quantity
Solution x y 𝑠1 𝑠2 𝑠3
8 y 0.5 1 0.1 0 0 10
0 𝑠2 3.5 0 -0.7 1 0 14
0 𝑠3 6.5 0 -0.5 0 1 40
Gross 𝑍𝑗 4 8 0.8 0 0 80
NET 𝐶𝑗- 𝑍𝑗 2 0 -0.8 0 0 Total
ProfitMax +? Yes/No Yes No No No No

20. STEP 4: Determine the pivot row
1. Compute the quantity ratio (𝑄 𝑟):
𝑄 𝑟= Q/pivot column
20 = 10/0.5
4 = 14/3.5
6.15385 = 40/6.5
2. Determine the minimum positive quantity ratio
4 = +minimum (20, 4, 6.15385)
= pivot row is 𝑠2
3. Determine the pivot number:
3.5 = intersection of pivot column and pivot
row

21. Table 2.1: Second Pivot Row
Solution
Mix
Pivot col
x
Quantity 𝑸𝒖𝒂𝒏𝒕𝒊𝒕𝒚
𝑷𝒊𝒗𝒐𝒕 𝒄𝒐𝒍
Min +?
Yes/No
y 0.5 10 20 No
𝑠2 3.5 14 4 Yes
𝑠3 6.5 40 6.15385 No

22. STEP 5: Develop the third tableau (Table 4).
1. Replace the pivot row with the pivot column in
solution column:
Exit = 0𝑠2
Enter = 6x
2. Replace the 𝑠2 row of the second tableau with the x
row in the third tableau:
x row = 𝑠2 row of the second tableau/pivot number
1 = 3.5/3.5 0.28571 = 1/3.5
0 = 0/3.5 0 = 0/3.5
-0.2 = -0.7/3.5 4 = 14/3.5

23. 3. Replace the y row of the second tableau with
new
values in the third tableau:
New y row = old y row – (number in old y row
and pivot column)(x row)
0 = 0.5 – 0.5(1)
1 = 1 – 0.5(0)
0.2 = 0.1 – 0.5(-0.2)
-0.14286 = 0 – 0.5(0.28571)
0 = 0 – 0.5(0)
8 = 10 – 0.5(4)

24. 4. Replace the 𝑠3 row of the second tableau with
new
values in the third tableau:
New 𝑠3 row = old 𝑠3 row – (number in old 𝑠3 row
and pivot column)(x row)
0 = 6.5 – 6.5(1)
0 = 0 – 6.5(0)
0.8 = -0.5 – 6.5(-0.2)
-1.85714 = 0 – 6.5(0.28571)
1 = 1 – 6.5(0)
14 = 40 – 6.5(4)

25. 5. Compute the 𝑍𝑗 values:
𝑍𝑗 = sumproduct (basic 𝐶𝑗 column, variable
column)
6 = 8(0) + 6(1) + 0(0)
8 = 8(1) + 6(0) + 0(0)
0.4 = 8(0.2) + 6(-0.2) + 0(0.8)
0.57143 = 8(-0.14286) + 6(0.28571) + 0(-
1.85714)
0 = 8(0) + 6(0) + 0(1)
88 = 8(8) + 6(4) + 0(14)
= 88 dollar of total profit for this solution

26. 6. Compute the (𝐶𝑗- 𝑍𝑗) values:
𝐶𝑗- 𝑍𝑗 = 𝐶𝑗 row − 𝑍𝑗 row
0 = 6 – 6
0 = 8 – 8
-0.4 = 0 – 0.4
-0.57143 = 0 – 0.57143
0 = 0 – 0

27. 7. Determine the maximum positive (𝐶𝑗- 𝑍𝑗) value:
None = +maximum (0, 0, -0.4, -0.57143, 0)
= final tableau is reached
8. Determine the final solution:
y = 8 (8 cases of Women’s shampoo should be
produced per day)
x = 4 (4 cases of Men’s shampoo should be
produced
per day)
𝑠3= 14 (14 minutes of packing capacity are unused
per
day)
𝑍𝑗 = 88 (88 dollars is the total profit per day)

28. Table 4: Third Tableau
Thus, Geena should produce 4 cases of
Men’s shampoo and 8 cases of Women’s shampoo
per day at a total profit of 88 dollars, with 14
minutes of unused packing capacity.
Basic
𝐶𝑗
𝐶𝑗 6 8 0 0 0 Quantity
Solution x y 𝑠1 𝑠2 𝑠3
8 y 0 1 0.2 -0.14286 0 8
6 x 1 0 -0.2 0.28571 0 4
0 𝑠3 0 0 0.8 -1.85714 1 14
Gross 𝑍𝑗 6 8 0.4 0.57143 0 88
NET 𝐶𝑗- 𝑍𝑗 0 0 -0.4 -0.57143 0 Total
ProfitMax +? Yes/No None

29. Example 2: Nescafe
Harold is the Plant Supervisor of Nescafe and he
want to determine the production mix that will result to
maximum profit. He is able to determine the data necessary
for him to make a decision. It will take 9 minutes to roast 1
case of Classic Coffee and 7 minutes to roast 1 case of
Decaf Coffee and he has a total of 126 minutes available for
the roasting process per day. It will take 7 minutes to grind 1
case of Classic Coffee and 8 minutes to grind 1 case of
Decaf Coffee and he has a total of 112 minutes available for
the grinding process per day. It will take 6 minutes to pack 1
case of Classic Coffee and 11 minutes to pack 1 case of
Decaf Coffee and he has a total of 132 minutes available for
the packing process per day. He will earn 6 dollars for every
case of Classic Coffee produced and 4 dollars for every case
of Decaf Coffee produced.
How many cases of Classic Coffee and Decaf Coffee
should be produced per day to maximize profits? How much
is the total profit?

30. Table: Nescafe
Process/Produc
t
Mins per case Sign Mins per day
Classic Decaf
Roasting 9 7 ≤ 126
Grinding 7 8 ≤ 112
Packing 6 11 ≤ 132
Profit per case 6 4 = Max

31. Example 3: Century Tuna
Iola is the Operations Director of Century Tuna
and she wants to determine the production mix that will
result to maximum profit. She is able to determine the
data necessary for her to make a decision. It will take 5
minutes to cook 1 case of Regular Tuna and 12
minutes to cook 1 case of Spicy Tuna and she has a
total of 120 minutes available for the cooking process
per day. It will take 10 minutes to can 1 case of Regular
Tuna and 5 minutes to can 1 case of Spicy Tuna and
she has a total of 100 minutes available for the canning
process per day. It will take 7 minutes to label 1 case of
Regular Tuna and 6 minutes to label 1 case of Spicy
Tuna and she has a total of 84 minutes available for
the labeling process per day. She will earn 15 dollars
for every case of Regular Tuna produced and 10
dollars for every case of Spicy Tuna produced.
How many cases of Regular Tuna and Spicy
Tuna should be produced per day to maximize profits?
How much is the total profit?

32. Table: Century Tuna
Process/Produc
t
Mins per case Sign Mins per day
Regular Spicy
Cooking 5 12 ≤ 120
Canning 10 5 ≤ 100
Labeling 7 6 ≤ 84
Profit per case 15 10 = Max

33. References:
1) Quantitative Techniques for Business
by Priscilla S. Altares, et.,al.
2) Quantitative Techniques in
Management
by Jonathan B. Cabero, et., al.
3) Quantitative Decision Models
by Edwin J. Loma
4) Quantitative Business Method
by David Anderson