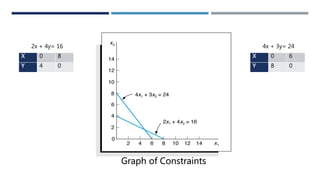
This document describes a linear programming problem (LPP) to minimize cost. The problem involves determining the optimal amounts of two fertilizer brands, SuperGro and CropQuick, to purchase to minimize total cost while meeting nitrogen and phosphate requirements. The LPP constructs decision variables for amounts of each brand, an objective function to minimize total cost, and constraints on nitrogen and phosphate levels. The optimal solution is to purchase 8 bags of CropQuick for a minimum total cost of 24.

1. LINEAR PROGRAMMING PROBLEM
(LPP)
TOPIC: COST MINIMIZATION

2. INTRODUCTION
 Linear programming is a mathematical technique used to find the best possible solution in allocating
limited resources (constraints) to achieve maximum profit or minimum cost by modelling linear
relationships.
 Model formulation steps :
• Define the decision variables
• Construct the objective function
• Formulate the constraints
• Find the feasible solution
• Calculate the value of the objective function at each of the vertices of feasible solution area to
determine which of them has the maximum or minimum values

3. MODEL COMPONENTS
 Decision variables – mathematical symbols representing levels of activity of a firm.
 Objective function – a linear mathematical relationship describing an objective of the firm, in terms of
decision variables - this function is to be maximized or minimized.
 Constraints – requirements or restrictions placed on the firm by the operating environment, stated in
linear relationships of the decision variables.
 Parameters – numerical coefficients and constants used in the objective function and constraints.

4. LP MODEL FORMULATION
 Two brands of fertilisers available: SuperGro & CropQuick
 Field requires at least 16 kgs of nitrogen and 24 kgs of phosphate
 SuperGro costs ₹6 per bag and CropQuick costs ₹3 per bag
 SuperGro has 2 kgs of nitrogen & 4 kgs of phosphate
 CropQuick has 4 kgs of nitrogen & 3 kgs of phosphate
 Problem: How much of each brand to buy to minimize total cost of fertiliser ?
Brand Nitrogen Phosphate
SuperGro 2 4
CropQuick 4 3

5.  Decision Variables
x = No. of bags of SuperGro
y = No. of bags of CropQuick
 Objective Function
Minimize, z = 6x + 3y
 Constraints
2x + 4y >= 16 (nitrogen)
4x + 3y >= 24 (phosphate)
x, y >= 0 (non-negativity constraint)

6. Graph of Constraints
X 0 6
Y 8 0
X 0 8
Y 4 0
4x + 3y= 242x + 4y= 16

7. Feasible Solution Area

8. Optimum Solution
Points Z
A (0,8) 24
B (4.8,1.6) 33.6
C (8,0) 48
z = 6x + 3y
So, 8 kgs of CropQuick should be bought to
minimise total cost of fertiliser.

9. Thank You