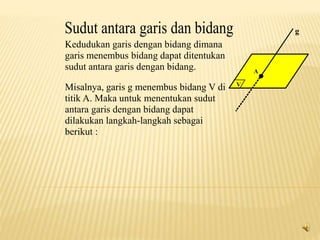
Dokumen tersebut membahas tentang penentuan sudut antara dua bidang dan garis dengan bidang dalam ruang tiga dimensi. Dijelaskan cara menentukan sudut antar dua bidang yang berpotongan dengan menetapkan garis potong dan membuat garis tegak lurus pada titik potong. Kemudian sudut antara dua garis tegak lurus tersebut merupakan sudut antara kedua bidang.

1. SUDUT ANTARA DUA
BIDANG
Oleh:
Dwi Andriyani
4101012015
Pendidikan Matematika
6. Menentukan kedudukan, jarak, dan besar sudut yang melibatkan titik,
garis, dan bidang dalam ruang dimensi tiga
6.3 Menentukan besar sudut antara garis dan bidang dan antara dua
bidang dalam ruang dimensi tiga

2. PPG – Pend. Matematika UNNES

3. SUDUT ANTARA DUA BIDANG
 Menggambar sudut antara dua bidang
yang berpotongan
 enentukan sudut antara dua bidang yang
berpotongan
 Menentukan sudut antara dua bidang
dalam ruang dimensi tiga

4. SUDUT ANTARA DUA BIDANG

5. PENDIDIKAN MATEMATIKA
UNIVERSITAS NEGERI SEMARANG
PRASYARAT

6. TEOREMA PROYEKSI
a. Kuadrat sisi siku – siku sama dengan hasil kali
proyeksinya ke sisi miring dan sisi miring sendiri.
c2 = pa atau b2 = qa
b. Kuadrat garis tinggi ke sisi miring sama dengan hasil
kali bagian sisi miring. t2 = pq
c. Hasil kali sisi siku – siku sama dengan hasil kali sisi
miring dan garis tinggi ke sisi miring itu. bc = ta
d. Kuadrat sisi miring sama dengan jumlah kuadrat kedua
sisi yang lain. a2 = b2 + c2
a
q
t pb
c
C
BA

7. ATURAN SINUS
ATURAN KOSINUS

8. Kedudukan garis dengan bidang dimana
garis menembus bidang dapat ditentukan
sudut antara garis dengan bidang.

9. Misalnya, garis g menembus bidang V di
titik A. Maka untuk menentukan sudut
antara garis dengan bidang dapat
dilakukan langkah-langkah sebagai
berikut :
Kedudukan garis dengan bidang dimana
garis menembus bidang dapat ditentukan
sudut antara garis dengan bidang.
V
g
A

10. Kedudukan garis dengan bidang dimana
garis menembus bidang dapat ditentukan
sudut antara garis dengan bidang.
• Tetapkan satu titik sembarang pada garis g di luar bidang
V, misalkan titik B
Misalnya, garis g menembus bidang V di
titik A. Maka untuk menentukan sudut
antara garis dengan bidang dapat
dilakukan langkah-langkah sebagai
berikut :
V
g
A
B

11. • Tetapkan satu titik sembarang pada garis g di luar bidang
V, misalkan titik B
Kedudukan garis dengan bidang dimana
garis menembus bidang dapat ditentukan
sudut antara garis dengan bidang.
Misalnya, garis g menembus bidang V di
titik A. Maka untuk menentukan sudut
antara garis dengan bidang dapat
dilakukan langkah-langkah sebagai
berikut :
• Proyeksikan titik B pada bidang V, misalkan titik B’
V
g
A
B’
B

12. • Hubungkan titik A dengan titik B’
Kedudukan garis dengan bidang dimana
garis menembus bidang dapat ditentukan
sudut antara garis dengan bidang.
• Tetapkan satu titik sembarang pada garis g di luar bidang
V, misalkan titik B
Misalnya, garis g menembus bidang V di
titik A. Maka untuk menentukan sudut
antara garis dengan bidang dapat
dilakukan langkah-langkah sebagai
berikut :
• Proyeksikan titik B pada bidang V, misalkan titik B’
V
g
A
B’
B
a

13. • Hubungkan titik A dengan titik B’
Kedudukan garis dengan bidang dimana
garis menembus bidang dapat ditentukan
sudut antara garis dengan bidang.
• Tetapkan satu titik sembarang pada garis g di luar bidang
V, misalkan titik B
Misalnya, garis g menembus bidang V di
titik A. Maka untuk menentukan sudut
antara garis dengan bidang dapat
dilakukan langkah-langkah sebagai
berikut :
• Proyeksikan titik B pada bidang V, misalkan titik B’
V
g
A
B’
B
a
• Sudut BAB’ merupakan sudut antara garis g dan bidang V

14. HUBUNGAN ANTARA BIDANG-BIDANG
Hubungan antara dua bidang yang memungkinkan jika
diketahui bidang V dan bidang W :
1. Bidang V dan bidang W berhimpit, (semua titik pada
bidang V terletak pada bidang W, dan sebaliknya)
dipandang sebagai sebuah bidang saja
2. Bidang V dan bidang W sejajar, kedua bidang tidak
memiliki titik persekutuan
3. Bidang V dan bidang W berpotongan. , perpotongan
kedua bidang berupa garis lurus yang disebut garis
potong atau garis persekutuan yang dilambangkan
dengan (V,W)

15. Sudut antara bidang U dan bidang V
(berpotongan) dapat ditentukan dengan
cara sebagai berikut :
V
U

16. Sudut antara bidang U dan bidang V
(berpotongan) dapat ditentukan dengan
cara sebagai berikut :
• Tetapkan garis persekutuan
bidang U dengan bidang V
yaitu (U,V)
V
U
(V,U)
Q

17. Sudut antara bidang U dan bidang V
(berpotongan) dapat ditentukan dengan
cara sebagai berikut :
• Tetapkan garis persekutuan
bidang U dengan bidang V
yaitu (U,V)
• Tetapkan sebuah titik P pada
garis (U,V)
V
U
(V,U)
P

18. Sudut antara bidang U dan bidang V
(berpotongan) dapat ditentukan dengan
cara sebagai berikut :
• Tetapkan garis persekutuan
bidang U dengan bidang V
yaitu (U,V)
• Tetapkan sebuah titik P pada
garis (U,V)
• Pada bidang U, buat garis
melalui P tegak lurus garis
(U,V) yaitu PQ
V
U
(V,U)
R
Q
P

19. Sudut antara bidang U dan bidang V
(berpotongan) dapat ditentukan dengan
cara sebagai berikut :
• Tetapkan garis persekutuan
bidang U dengan bidang V
yaitu (U,V)
• Tetapkan sebuah titik P pada
garis (U,V)
• Pada bidang V, buat garis
melalui P tegak lurus garis
(U,V) yaitu PR
• Pada bidang U, buat garis
melalui P tegak lurus garis
(U,V) yaitu PQ
V
U
(V,U)
R
Q
P

20. Sudut antara bidang U dan bidang V
(berpotongan) dapat ditentukan dengan
cara sebagai berikut :
• Tetapkan garis persekutuan
bidang U dengan bidang V
yaitu (U,V)
• Tetapkan sebuah titik P pada
garis (U,V)
• Pada bidang V, buat garis
melalui P tegak lurus garis
(U,V) yaitu PR
• Sudut QPR adalah sudut
bidang U dan bidang V
• Pada bidang U, buat garis
melalui P tegak lurus garis
(U,V) yaitu PQ V
U
(V,U)
R
Q
P

21. Kubus ABCD.EFGH dengan panjang rusuk 6 cm. Titik P
di tengah EF dan R di tengah GH. Tentukan sudut antara
bidang ADRP dengan bidang BCRP
A
H G
C
B
E F
D

22. Kubus ABCD.EFGH dengan panjang rusuk 6 cm. Titik P
di tengah EF dan R di tengah GH. Tentukan sudut antara
bidang ADRP dengan bidang BCRP
Jawab :
• Tentukan garis persekutuan bidang
ADRP dengan bidang BCRP yaitu RP
A
H G
C
B
E F
D
R
P

23. Kubus ABCD.EFGH dengan panjang rusuk 6 cm. Titik P
di tengah EF dan R di tengah GH. Tentukan sudut antara
bidang ADRP dengan bidang BCRP
Jawab :
• Tentukan garis persekutuan bidang
ADRP dengan bidang BCRP yaitu RP
• Tetapkan sebuah titik T pada garis
RP (T di tengah RP)
A
H G
C
B
E F
D
R
P
T

24. Kubus ABCD.EFGH dengan panjang rusuk 6 cm. Titik P
di tengah EF dan R di tengah GH. Tentukan sudut antara
bidang ADRP dengan bidang BCRP
Jawab :
• Tentukan garis persekutuan bidang
ADRP dengan bidang BCRP yaitu RP
• Tetapkan sebuah titik T pada garis
RP (T di tengah RP)
• Pada bidang BCRP, buat garis melalui T tegak lurus RP
yaitu TL
A
H G
C
B
E F
D
R
P
T
L

25. Kubus ABCD.EFGH dengan panjang rusuk 6 cm. Titik P
di tengah EF dan R di tengah GH. Tentukan sudut antara
bidang ADRP dengan bidang BCRP
Jawab :
• Tentukan garis persekutuan bidang
ADRP dengan bidang BCRP yaitu RP
• Tetapkan sebuah titik T pada garis
RP (T di tengah RP)
• Pada bidang BCRP, buat garis melalui T tegak lurus RP
yaitu TL
• Pada bidang ADRP, buat garis melalui T tegak lurus RP
yaitu TK
A
H G
C
B
E F
D
R
P
K
T
L

26. • Sudut KTL merupakan sudut antara dua bidang
Kubus ABCD.EFGH dengan panjang rusuk 6 cm. Titik P
di tengah EF dan R di tengah GH. Tentukan sudut antara
bidang ADRP dengan bidang BCRP
Jawab :
• Tentukan garis persekutuan bidang
ADRP dengan bidang BCRP yaitu RP
• Tetapkan sebuah titik T pada garis
RP (T di tengah RP)
• Pada bidang BCRP, buat garis melalui T tegak lurus RP
yaitu TL
• Pada bidang ADRP, buat garis melalui T tegak lurus RP
yaitu TK
A
H G
C
B
E F
D
R
P
K
T
L

27. 1. Diketahui kubus ABCD. EFGH.
a.Gambar sudut antara bidang ABCD dengan bidang
ABGH!
b.Tentukan besar sudut antara bidang ABCD dengan
bidang ABGH!

28. PPG – Pend. Matematika UNNES

29. PPG – Pend. Matematika UNNES
Nama : Dwi Andriyani
Nim : 4101012015
Hp : 085777119219
Email : wiex_ext@yahoo.com
Let’s do whatever that we can do!
Jurusan matematika
Universitas negeri semarang