Downloaded 4,965 times
Uploaded byMeelu Qazi
Chapter 8 mechanical failure
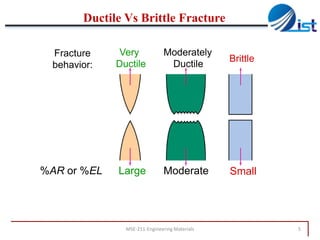
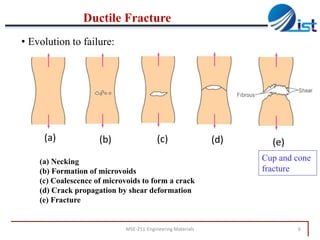
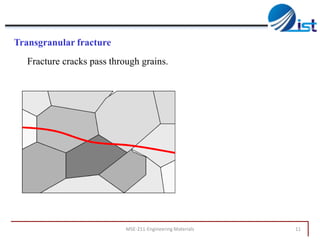
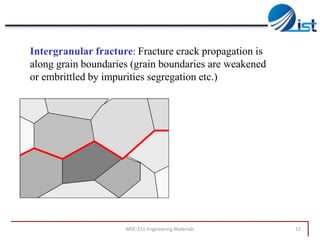
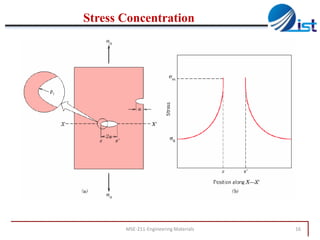
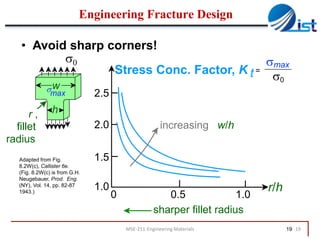
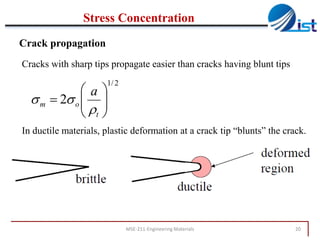
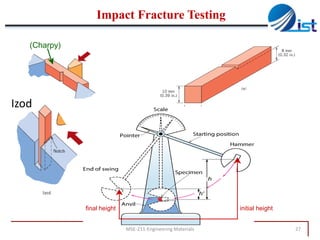
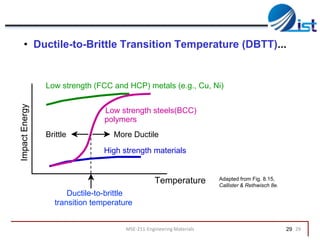
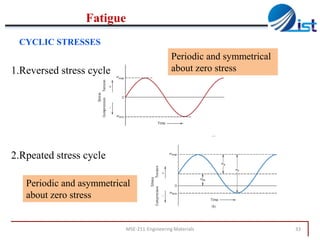
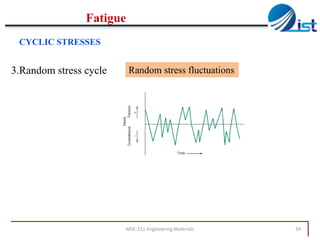
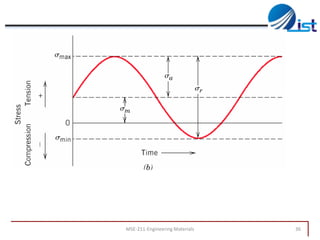
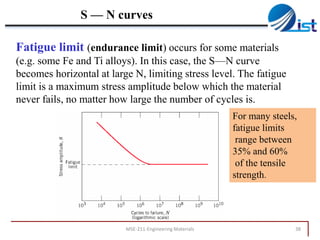
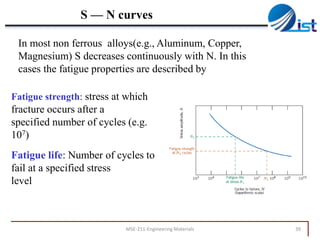
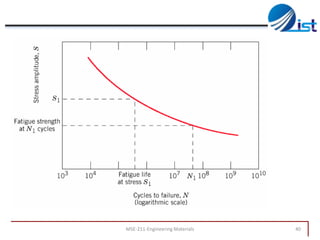
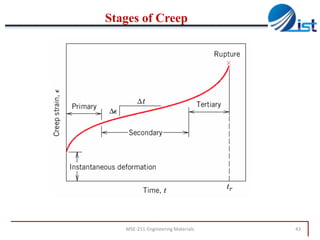
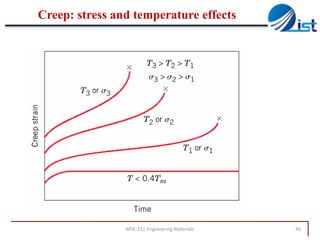
The document discusses mechanical failure and fracture in materials. It addresses how cracks form and propagate, leading to brittle or ductile fracture depending on the material. Stress concentration at crack tips is a key factor. Fracture toughness and impact testing methods are introduced to characterize a material's resistance to fracture. Fatigue failure from cyclic stresses often initiates at flaws and can occur at stresses below typical strength values. S-N curves relate the cyclic stress amplitude to the lifetime of a material. Temperature and loading conditions also influence failure behavior.
More Related Content
![ME 312 Mechanical Machine Design [Screws, Bolts, Nuts]](https://cdn.slidesharecdn.com/ss_thumbnails/me312-dsulec10-screws-170213050612-thumbnail.jpg?width=640&height=640&fit=bounds)
Similar to Chapter 8 mechanical failure
Chapter 8 mechanical failure
- 1. Mechanical Failure ISSUES TOADDRESS... Chapter reading 8 • How do cracks that lead to failure form? • How is fracture resistance quantified? How do the fracture resistances of the different material classes compare? • How do we estimate the stress to fracture? • How do loading rate, loading history, and temperature affect the failure behavior of materials? Ship-cyclic loading from waves. Computer chip-cyclic thermal loading. MSE-211-Engineering Materials Hip implant-cyclic loading from walking. 1 1
- 2. Mechanical Failure Why studyfailure? Design of a component or structure: Minimize failure possibility It can be accomplished by understanding the mechanics of failure modes and applying appropriate design principles. Failure cost 1. Human life 2. Economic loss 3.Unavailability of service Failure causes: 1. Improper material selection 2. Inadequate design 3. Processing Regular inspection, repair and replacement critical to safe design MSE-211-Engineering Materials 2
- 3. Fracture Fracture is theseparation of a body into two or more pieces in response to an imposed stress Steps in Fracture: Crack formation Crack propagation MSE-211-Engineering Materials 3
- 4. Fracture Modes Depending onthe ability of material to undergo plastic deformation before the fracture two fracture modes can be defined - ductile or brittle. Ductile fracture - most metals (not too cold): Extensive plastic deformation ahead of crack Crack is “stable”: resists further extension unless applied stress is increased Brittle fracture - ceramics, ice, cold metals: Relatively little plastic deformation Crack is “unstable”: propagates rapidly without increase in applied stress Ductile fracture is preferred in most applications MSE-211-Engineering Materials 4
- 5. Ductile Vs BrittleFracture Fracture behavior: Very Ductile Moderately Ductile Brittle %AR or %EL Large Moderate Small MSE-211-Engineering Materials 5
- 6. Ductile Fracture • Evolutionto failure: (a) (b) (c) (a) Necking (b) Formation of microvoids (c) Coalescence of microvoids to form a crack (d) Crack propagation by shear deformation (e) Fracture MSE-211-Engineering Materials (d) (e) Cup and cone fracture 6
- 7. Ductile Vs BrittleFracture ductile fracture brittle fracture (Cup-and-cone fracture in Al) Brittle fracture in a mild steel MSE-211-Engineering Materials 7
- 8. Ductile Fracture (a) SEMimage showing spherical dimples resulting from a uniaxial tensile load representing microvoids. (b) SEM image of parabolic dimples from shear loading. MSE-211-Engineering Materials 8
- 9. Brittle Fracture Arrows indicatepoint at failure origination Distinctive pattern on the fracture surface: V-shaped “chevron” markings point to the failure origin. MSE-211-Engineering Materials 9
- 10. Brittle Fracture Lines orridges that radiate from the origin of the crack in a fanlike pattern MSE-211-Engineering Materials 10
- 11. Transgranular fracture Fracture crackspass through grains. MSE-211-Engineering Materials 11
- 12. Intergranular fracture: Fracturecrack propagation is along grain boundaries (grain boundaries are weakened or embrittled by impurities segregation etc.) MSE-211-Engineering Materials 12
- 13. Example: Pipe Failures •Ductile failure: -- one piece -- large deformation • Brittle failure: -- many pieces -- small deformations MSE-211-Engineering Materials 13 13 13
- 14. Fracture Mechanics Studies therelationships between: material properties stress level crack producing flaws crack propagation mechanisms MSE-211-Engineering Materials 14
- 15. Stress Concentration Measured fracturestrength is much lower than predicted by calculations based on atomic bond energies. This discrepancy is explained by the presence of flaws or cracks in the materials. The flaws act as stress concentrators or stress raisers, amplifying the stress at a given point. The magnitude of amplification depends on crack geometry and orientation. MSE-211-Engineering Materials 15
- 16.
- 17. Stress Concentration If thecrack is similar to an elliptical hole through plate, and is oriented perpendicular to applied stress, the maximum stress, at crack tip 1/ 2 a s m 2s o where t t = radius of curvature so = applied stress sm = stress at crack tip a = length of surface crack or ½ length of internal crack MSE-211-Engineering Materials 17
- 18. Stress Concentration 1/ 2 a sm 2s o t (1) The stress concentration factor is A measure of the degree to which an external stress is amplified at the tip of a crack. a sm 2so Ktso t 1/ 2 Rearranging equation 1 MSE-211-Engineering Materials 18
- 19. Engineering Fracture Design •Avoid sharp corners! s smax Stress Conc. Factor, K t = s0 sw max r, fillet radius 2.5 h Adapted from Fig. 8.2W(c), Callister 6e. (Fig. 8.2W(c) is from G.H. Neugebauer, Prod. Eng. (NY), Vol. 14, pp. 82-87 1943.) 2.0 increasing w/h 1.5 1.0 0 0.5 1.0 sharper fillet radius MSE-211-Engineering Materials r/h 19 19
- 20. Stress Concentration Crack propagation Crackswith sharp tips propagate easier than cracks having blunt tips 1/ 2 a s m 2s o t In ductile materials, plastic deformation at a crack tip “blunts” the crack. MSE-211-Engineering Materials 20
- 21. Stress Concentration Crack propagation Criticalstress for crack propagation γs = specific surface energy When the tensile stress at the tip of crack exceeds the critical stress value the crack propagates and results in fracture. MSE-211-Engineering Materials 21
- 22. EXAMPLE PROBLEM 8.1Page 244 A relatively large plate of a glass is subjected to a tensile stress of 40 MPa. If the specific surface energy and modulus of elasticity for this glass are 0.3 J/m2 and 69 GPa, respectively, determine the maximum length of a surface flaw that is possible without fracture. 𝐸 = 69 𝐺𝑃𝑎 𝛾 𝑠 =0.3 J/m2 𝜎 = 40 𝑀𝑃𝑎 Rearranging the equation 2𝐸𝛾 𝑠 𝑎= 𝜋𝜎 2 𝑎 = 8.2 * 10-6 m MSE-211-Engineering Materials 22
- 23. Home Work Problems ExerciseProblems 8.1-8.4 MSE-211-Engineering Materials 23
- 24. Fracture Toughness • Fracturetoughness measures a material’s resistance to fracture when a crack is present. • It is an indication of the amount of stress required to propagate a preexisting flaw. 𝐾 𝑐 = 𝜎 𝑐 𝜋𝑎 𝐾 𝑐 = Fracture toughness MSE-211-Engineering Materials 24
- 25. Fracture Toughness 𝑲 𝒄is a material property depends on temperature, strain rate and microstructure. The magnitude of Kc diminishes with increasing strain rate and decreasing temperature. Improvement in yield strength wrought by alloying and strain hardening generally produces corresponding decrease in Kc . Kc normally increases with reduction in grain size as composition and other microstructural variables are maintained constant. MSE-211-Engineering Materials 25
- 26. Impact Fracture Testing Testingfracture characteristics under high strain rates Two standard tests, the Charpy and Izod, measure the impact energy (the energy required to fracture a test piece under an impact load), also called the notch toughness MSE-211-Engineering Materials 26
- 27. Impact Fracture Testing (Charpy) Izod finalheight initial height MSE-211-Engineering Materials 27
- 28. Ductile-to- brittle transition Astemperature decreases a ductile material can become brittle - ductile-to-brittle transition. The ductile-to-brittle transition can be measured by impact testing: the impact energy needed for fracture drops suddenly over a relatively narrow temperature range – temperature of the ductile-tobrittle transition. The ductile to-brittle transition is related to the temperature dependence of the measured impact energy absorption MSE-211-Engineering Materials 28
- 29. • Ductile-to-Brittle TransitionTemperature (DBTT)... Impact Energy Low strength (FCC and HCP) metals (e.g., Cu, Ni) Low strength steels(BCC) polymers Brittle More Ductile High strength materials Temperature Adapted from Fig. 8.15, Callister & Rethwisch 8e. Ductile-to-brittle transition temperature MSE-211-Engineering Materials 29 29
- 30. Design Strategy: Stay AboveThe DBTT! • Pre-WWII: The Titanic • WWII: Liberty ships • Problem: Steels were used having DBTT’s just below room temperature. MSE-211-Engineering Materials 30
- 31. Fatigue Fatigue Failure under fluctuating/ cyclic stresses e.g., bridges, aircraft, machine components, automobiles,etc.. • Stress varies with time. smax sm smin MSE-211-Engineering Materials s S time 31
- 32. Fatigue Fatigue failure canoccur at loads considerably lower than tensile or yield strengths of material under a static load. Estimated to causes 90% of all failures of metallic structures Fatigue failure is brittle-like (relatively little plastic deformation) - even in normally ductile materials. Thus sudden and catastrophic! Fatigue failure proceeds in three distinct stages: crack initiation in the areas of stress concentration (near stress raisers), incremental crack propagation, final catastrophic failure. MSE-211-Engineering Materials 32
- 33. Fatigue CYCLIC STRESSES Periodic andsymmetrical about zero stress 1.Reversed stress cycle 2.Rpeated stress cycle Periodic and asymmetrical about zero stress MSE-211-Engineering Materials 33
- 34. Fatigue CYCLIC STRESSES 3.Random stresscycle Random stress fluctuations MSE-211-Engineering Materials 34
- 35. Fatigue CYCLIC STRESSES Mean stress(𝜎 𝑚 ) MSE-211-Engineering Materials 35
- 36.
- 37. Fatigue S — Ncurves (stress — number of cycles to failure) Fatigue properties of a material (S-N curves) are tested in rotating-bending tests in fatigue testing apparatus Result is commonly plotted as S (stress) vs. N (number of cycles to failure) MSE-211-Engineering Materials 37
- 38. S — Ncurves Fatigue limit (endurance limit) occurs for some materials (e.g. some Fe and Ti alloys). In this case, the S—N curve becomes horizontal at large N, limiting stress level. The fatigue limit is a maximum stress amplitude below which the material never fails, no matter how large the number of cycles is. For many steels, fatigue limits range between 35% and 60% of the tensile strength. MSE-211-Engineering Materials 38
- 39. S — Ncurves In most non ferrous alloys(e.g., Aluminum, Copper, Magnesium) S decreases continuously with N. In this cases the fatigue properties are described by Fatigue strength: stress at which fracture occurs after a specified number of cycles (e.g. 107) Fatigue life: Number of cycles to fail at a specified stress level MSE-211-Engineering Materials 39
- 40.
- 41. Fatigue Fracture surface characteristics Beachmarks and striations MSE-211-Engineering Materials 41
- 42. Creep Creep is atime-dependent and permanent deformation of materials when subjected to a constant load or stress. For metals it becomes important at a high temperature (> 0.4 Tm). Examples: turbine blades, steam generators, high pressure steam lines. Polymers are specially sensitive to creep. For details read the book pages 265-267 MSE-211-Engineering Materials 42
- 43. Stages of Creep MSE-211-EngineeringMaterials 43
- 44. Stages of Creep 1.Instantaneous deformation, mainly elastic. 2. Primary/transient creep. Slope of strain vs. time decreases with time: strain-hardening 3. Secondary/steady-state creep. Rate of straining is Constant 4. Tertiary. Rapidly accelerating strain rate up to failure: formation of internal cracks, voids, grain boundary separation, necking, etc. MSE-211-Engineering Materials 44
- 45. Parameters of creepbehavior The stage of secondary/steady-state creep is of longest . ∆𝜺 .is the ∆𝒕 duration and the steady-state creep rate 𝜺 𝒔 = most important parameter of the creep behavior in long-life applications e.g. nuclear power plant component. Another parameter, especially important in short-life creep situations, is time to rupture, or the rupture lifetime, tr.. e.g., turbine blades in military aircraft and rocket motor nozzles, etc…. MSE-211-Engineering Materials 45
- 46. Creep: stress andtemperature effects MSE-211-Engineering Materials 46