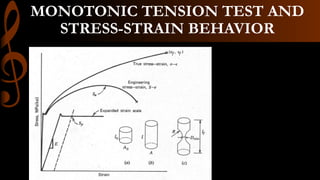
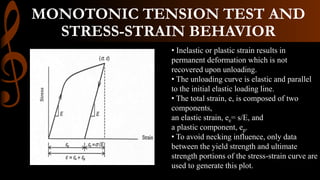
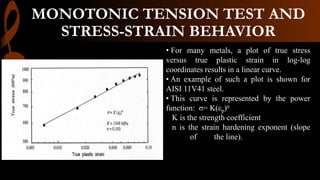
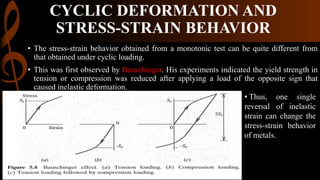
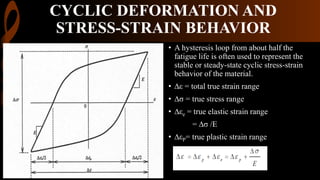
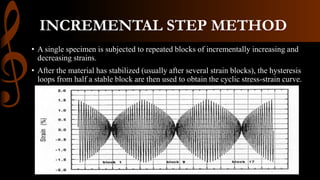
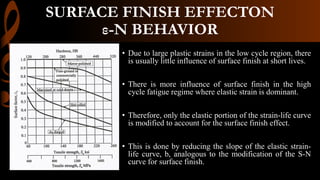
1) A monotonic tension test subjects a specimen to increasing tensile force until fracture to obtain its stress-strain behavior. For larger strains, true stress and strain must account for changes in specimen dimensions rather than engineering stress and strain. 2) Cyclic strain-controlled testing better characterizes fatigue behavior by directly controlling and measuring strain. Hysteresis loops provide the cyclic stress-strain response. 3) The strain-life approach relates the fatigue life of notched components to the life of unnotched specimens experiencing the same strain levels. It assesses fatigue damage directly based on local strain measurements.

1. STRAIN LIFE APPROACH
Dr. RUDRESH M
ASSISTANT PROFESSOR
DEPARTMENT OF AERONAUTICAL ENGINEEIRNG
DAYANANDA SAGAR COLLEGE OF ENGINEERING

2. MONOTONIC TENSION TEST
AND STRESS-STRAIN BEHAVIOR
• Monotonic behavior is obtained from a tension test where a specimen with circular or
rectangular cross section within the uniform gage length is subjected to a monotonically
increasing tensile force until it fractures.
• Monotonic uni-axial stress-strain behavior can be based on "engineering" stress-strain or
"true" stress-strain relationships.
• The difference is in using original versus instantaneous gage section dimensions.
• For small strains, less than about 2 percent, the "engineering" stress, S, is approximately
equal to the "true" stress, σ, and the "engineering" strain, e, is approximately equal to the
"true" strain, ε.
• No distinction between "engineering" and "true" components is needed for these small
strains.
• For larger strains the differences become appreciable.

3. MONOTONIC TENSION TEST AND
STRESS-STRAIN BEHAVIOR

4. MONOTONIC TENSION TEST AND
STRESS-STRAIN BEHAVIOR
• Inelastic or plastic strain results in
permanent deformation which is not
recovered upon unloading.
• The unloading curve is elastic and parallel
to the initial elastic loading line.
• The total strain, e, is composed of two
components,
an elastic strain, ee= s/E, and
a plastic component, ep.
• To avoid necking influence, only data
between the yield strength and ultimate
strength portions of the stress-strain curve are
used to generate this plot.

5. MONOTONIC TENSION TEST AND
STRESS-STRAIN BEHAVIOR
• For many metals, a plot of true stress
versus true plastic strain in log-log
coordinates results in a linear curve.
• An example of such a plot is shown for
AISI 11V41 steel.
• This curve is represented by the power
function: σ= K(εp)n
K is the strength coefficient
n is the strain hardening exponent (slope
of the line).

6. MONOTONIC TENSION TEST AND
STRESS-STRAIN BEHAVIOR
• The total true strain is given by:
• This type of true stress-true strain relationship is often referred to as the Ramberg-
Osgood relationship.
• Value of n gives a measure of the material’s work hardening behavior and is usually
between 0 and 0.5.

7. STRAIN-CONTROLLED TEST
METHODS
• An important aspect of the fatigue process is plastic
deformation. Fatigue cracks usually nucleate from
plastic straining in localized regions.
• Therefore, cyclic strain-controlled tests can better
characterize fatigue behavior of a material than cyclic
stress-controlled tests, particularly in the low cycle
fatigue region and/or in notched members.
• Strain-controlled fatigue testing has become very
common, even though the testing equipment and
control are more complicated than the traditional load
or stress-controlled testing.

8. STRAIN-CONTROLLED TEST
METHODS
• Strain-controlled testing is usually conducted on a servo-controlled closed-
loop testing machine.
• An un-notched uniform gage, smooth specimen is subjected to axial
straining.
• An extensometer is attached to the uniform gage length to control and
measure strain over the gage section.
• A standard strain-controlled test consists of constant amplitude completely
reversed straining at a constant or nearly constant strain rate.
• The most common strain-time control signals used are triangular (saw
tooth) and sinusoidal waveforms.
• Stress response generally changes with continued cycling. Stress and plastic
strain variations are usually recorded periodically throughout the test and
cycling is continued until fatigue failure occurs.

9. CYCLIC DEFORMATION AND
STRESS-STRAIN BEHAVIOR
• The stress-strain behavior obtained from a monotonic test can be quite different from
that obtained under cyclic loading.
• This was first observed by Bauschinger. His experiments indicated the yield strength in
tension or compression was reduced after applying a load of the opposite sign that
caused inelastic deformation.
• Thus, one single
reversal of inelastic
strain can change the
stress-strain behavior
of metals.

10. CYCLIC DEFORMATION AND
STRESS-STRAIN BEHAVIOR
• The stress strain response of metals is often drastically altered due to repeated
loading. Depending on the initial conditions of a metal( quenched and tempered or
annealed) and the test conditions , a) cyclically harden b) cyclically soften c)
cyclically stable d) mixed behavior.
• The extent and rate of cyclic hardening or softening under strain-controlled testing
conditions can be evaluated by recording stress variation as a function of cycles as
shown in Fig.
a) Constant strain amplitude b) cyclic hardening c) cyclic softening

11. CYCLIC DEFORMATION AND
STRESS-STRAIN BEHAVIOR
• Cyclic hardening indicates increased resistance to deformation.
• Cyclic softening indicates decreased resistance to deformation.
• Changes in cyclic deformation behavior are more pronounced at the beginning of
cyclic loading (transient behavior), but the material usually stabilizes gradually
(steady-state) with continued cycling.
• Such cyclic deformation behavior is referred to as cyclic transient behavior.

12. CYCLIC DEFORMATION AND
STRESS-STRAIN BEHAVIOR
• A hysteresis loop from about half the
fatigue life is often used to represent the
stable or steady-state cyclic stress-strain
behavior of the material.
• ∆ε = total true strain range
• ∆σ = true stress range
• ∆εe = true elastic strain range
= ∆σ /E
• ∆εP= true plastic strain range

13. CYCLIC DEFORMATION AND
STRESS-STRAIN BEHAVIOR
• A family of stabilized hysteresis loops at
different strain amplitudes is used to
obtain the cyclic stress-strain curve of a
material. The tips from the family of
multiple loops can be connected to form
the cyclic stress-strain curve as shown.
• This curve does not contain the monotonic
upper and lower yield points.
• Three methods commonly used to obtain
the cyclic stress-strain curve are:
Companion test method
Incremental step test method
Multiple step test method

14. COMPANION TEST METHOD
• Requires a series of test specimens, where each specimen is subjected to a constant
strain amplitude until failure.
• Half-life or near half-life hysteresis loops from each specimen and strain amplitude
are used to obtain the cyclic stress-strain curve.
• If the experimental program includes strain-controlled fatigue tests, the cyclic stress-
strain curve can be obtained from the same fatigue data using the companion
method.

15. INCREMENTAL STEP METHOD
• A single specimen is subjected to repeated blocks of incrementally increasing and
decreasing strains.
• After the material has stabilized (usually after several strain blocks), the hysteresis
loops from half a stable block are then used to obtain the cyclic stress-strain curve.

16. MULTIPLE STEP TEST METHOD
• It is similar to the incremental step test method, except rather than incrementally
increasing and decreasing strain in each block the strain amplitude is kept constant.
• Once cyclic stability is reached at the constant strain amplitude, the stable hysteresis
loop is recorded and strain amplitude is increased to a higher level.
• This process is repeated until sufficient number of stable hysteresis loops are
recorded to construct the cyclic stress-stain curve.

17. CYCLIC STRESS-STRAIN
BEHAVIOR
• Figure shows Cyclic and Monotonic
Stress-strain Curves for Several Materials
• Cyclic softening exists if the cyclic curve
is below the monotonic curve.
• Using monotonic properties in a cyclic
loading application for a cyclic softening
material can significantly underestimate
the extent of plastic strain which may
exist.
• Cyclic hardening is present if the cyclic
curve lies above the monotonic curve.
RUDRESH.M, DEPT. OF MECHANICAL, EWIT

18. CYCLIC STRESS-STRAIN
BEHAVIOR
• Similar to the monotonic deformation in a tension test, a plot of true stress
amplitude, σa, versus true plastic strain amplitude, ∆εp/2, in log-log coordinates for
most metals results in a linear curve which is represented by the power function:
• K'= cyclic strength coefficient,
• n'= cyclic strain hardening exponent
• The cyclic stress-strain equation represented by a Ramberg-Osgood type
relationship is then given by:
RUDRESH.M, DEPT. OF MECHANICAL, EWIT

19. STRAIN-BASED APPROACH TO LIFE
ESTIMATION, ε-N
• The strain-based approach to fatigue problems:
Is widely used at present.
Strain can be directly measured.
Application of this approach is common in notched member fatigue.
• Strain-life design method is based on relating the fatigue life of notched parts to the life of
small un-notched specimens cycled to the same strains as the material at the notch root.
Since fatigue damage is assessed directly in terms of local strain, this approach is also
called local strain approach.
Expected fatigue life can be determined knowing the strain-time history at the notch root
and smooth strain-life fatigue properties of the material.
The remaining fatigue crack growth life of a component can be analyzed using fracture
mechanics concepts .
RUDRESH.M, DEPT. OF MECHANICAL, EWIT

20. STRAIN-BASED APPROACH TO LIFE
ESTIMATION, ε-N
• Strain-life fatigue curves plotted on
log-log scales are shown schematically
in Fig.
• The total strain amplitude can be
resolved into elastic and plastic strain
components from the steady-state
hysteresis loops.
• Both the elastic and plastic curves can
be approximated as straight lines.
• At large strains or short lives, the
plastic strain component is
predominant, and at small strains or
longer lives the elastic strain
component is predominant.

21. STRAIN-BASED APPROACH TO LIFE
ESTIMATION, ε-N
• The straight line elastic behavior can be transformed to Basquin's eqn:
• The relation between plastic strain and life is (Manson-Coffin relationship):
• The intercepts of the two straight lines at 2Nf = 1 are σf
'/E for the elastic component and
εf
‘ for the plastic component.
• The slopes of the elastic and plastic lines are b and c, respectively.
• Therefore:

22. STRAIN-BASED APPROACH TO LIFE
ESTIMATION, ε-N
• The life where elastic and plastic
components of strain are equal is called
the transition fatigue life:
• For lives less than 2Nt the deformation
is mainly plastic, whereas for lives
larger than 2Nt the deformation is
mainly elastic.

23. DETERMINATION OF STRAIN-
LIFE FATIGUE PROPERTIES
• The fatigue strength coefficient, σf
', and fatigue strength exponent, b, are the intercept
and slope of the linear least squares fit to stress amplitude, ∆σ/2, versus reversals to
failure, 2Nf, using a log-log scale.
• Similarly, the fatigue ductility coefficient, εf
', and fatigue ductility exponent, c, are the
intercept and slope of the linear least squares fit to plastic strain amplitude, ∆εp/2,
versus reversals to failure, 2Nf, using a log-log scale.
• Plastic strain amplitudes can either be measured directly from half the width of stable
hysteresis loops, or calculated from

24. DETERMINATION OF STRAIN-
LIFE FATIGUE PROPERTIES
• When fitting the data to obtain the four strain-life properties, stress or plastic strain
amplitude should be treated as independent variables, whereas the fatigue life is the
dependent variable (i.e. fatigue life cannot be controlled and is dependent upon the
applied strain amplitude).
• The cyclic strength coefficient, K', and cyclic strain hardening exponent, n', are
obtained from fitting stable stress amplitude versus plastic strain amplitude data.
Rough estimates of K', and n‘ can also be calculated from the low cycle fatigue
properties by using:

25. DETERMINATION OF STRAIN-
LIFE FATIGUE PROPERTIES
• Strain-life equation has been approximated from monotonic tensile properties
(method of Universal Slopes):
• Another approximation that only uses hardness and E has been shown to provide
good agreement with experimental data for steels and is given by (Roessle and
Fatemi):

26. MEAN STRESSEFFECTS
• Strain-controlled cycling with a mean strain usually results in a mean stress which
may fully or partially relax with continued cycling.
• The relaxation is due to the presence of plastic deformation, and therefore, the rate
or amount of relaxation depends on the magnitude of the plastic strain amplitude
(more mean stress relaxation at larger strain amplitudes).

27. MEAN STRESSEFFECTS
• Stress relaxation is different
from the cyclic softening
phenomenon and can occur in a
cyclically stable material.
• Mean strain does not usually
affect the fatigue behavior
unless it results in a non-fully
relaxed mean stress.
• Since there is more mean stress
relaxation at higher strain
amplitudes due to larger plastic
strains, mean stress effect on
fatigue life is smaller in the low
cycle fatigue region and larger
in the high cycle fatigue region .

28. MEAN STRESSEFFECTS
• Several models dealing with mean stress effects on strain-life fatigue behavior are
available.
• Morrow’s parameter:
σm is the mean stress.
• An alternative version of Morrow’s mean stress parameter where both the elastic
and plastic terms are affected by the mean stress is given by:

29. MEAN STRESSEFFECTS
• Another equation suggested by Smith, Watson, and Topper(often called the SWT
parameter) is:
where σmax= σm+ σa and εa is the alternating strain.
• This equation is based on the assumption that for different combinations of strain
amplitude, εa, and mean stress, σm, the product σmaxεa remains constant for a given
life.
• If σmax is zero, this Eq. predicts infinite life, which implies that tension must be
present for fatigue fractures to occur.
• The SWT Eq. has been shown to correlate mean stress data better for a wide range
of materials and is regarded to be more promising for general use.
RUDRESH.M, DEPT. OF MECHANICAL, EWIT

30. OTHER FACTORS
INFLUENCING ε-NBEHAVIOR
• Similar to the S-N approach, in addition to the mean stress, many other factors can
influence strain-life fatigue behavior of a material. These include:
A. Stress concentrations
B. Residual stresses
C. Multi-axial stress states
D. Environmental effects
E. Size effects (similar to those in the S-N approach), and
F. Surface finish effects.
• The effects of many of these factors are similar to those on the S-N behavior.
RUDRESH.M, DEPT. OF MECHANICAL, EWIT

31. SURFACE FINISH EFFECTON
ε-N BEHAVIOR
• Due to large plastic strains in the low cycle region, there
is usually little influence of surface finish at short lives.
• There is more influence of surface finish in the high
cycle fatigue regime where elastic strain is dominant.
• Therefore, only the elastic portion of the strain-life curve
is modified to account for the surface finish effect.
• This is done by reducing the slope of the elastic strain-
life curve, b, analogous to the modification of the S-N
curve for surface finish.

32. THANK YOU