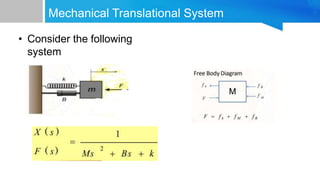
1. Translational mechanical systems consist of three basic elements: mass, spring, and dashpot. The transfer function is obtained by drawing a free-body diagram, writing Newton's law as a differential equation, and taking the Laplace transform. 2. Rotational mechanical systems also consist of three basic elements: moment of inertia, torsional spring, and dashpot. The transfer function is obtained similarly using torque and angular relationships. 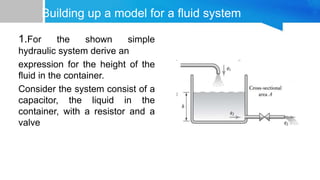3. Mathematical models of systems include differential equation models, transfer function models, and state-space models. Examples are shown for RLC circuits and fluid systems.

1. Unit-II
System Models and Responses

2. • A mathematicalmodel is a set of equations (usually differential
equations) that represents the dynamics of systems.
• In practice, the complexity of the system requires some
assumptions in the determination model.
• How do we obtain the equations?
• Physical law of the process
Examples:
– Mechanical system (Newton’slaws)
– Electrical system (Kirchhoff’slaws)

5. Basic Types ofMechanical Systems
• Translational System

6. • These systems mainly
consist of three basic
elements.
• Mass, spring and dashpot
or damper.

7. • A translational spring is a mechanical element that can be
deformed by an external force such that the deformation is
directly proportional to the force applied to it.

9. • Translational Mass is an
inertia element.
• A mechanical system
without mass does not
exist.
• If a force F is applied to a
mass and it is displacedto
x meters then the relation
b/w force and given by
Newton’s law.

10. • Dash Pot:
• If a force is applied on
dashpot B, then it is
opposed by an opposing
force due to friction of the
dashpot. This opposing
force is proportional to the
velocity of the body.
Assume mass and
elasticity are negligible.

11. Transfer function of Translational Mechanical Systems
• First, draw a free-body diagram, placing on the body all
forces that act on the body either in the direction of motion
or opposite to it.
• Second, use Newton’s law to form a differential equation
of motion by summing the forces and setting the sum
equal to zero.
• Finally, assuming zero initial conditions, we take the
Laplace transform of the differential equation, separate
the variables, and arrive at the transferfunction.

12. Rotational systems
• Spring-
T=Kθ
• Damper-
T=cω
• Moment of Inertia-
T=Iα

13. • Rotational Mechanical Systems
• These systems mainly consist of three basic elements. Those
are moment of inertia, torsional spring and dashpot.
Moment of Inertia
• In translational mechanical system, mass stores kinetic energy.
• Similarly, in rotational mechanical system, moment of inertia
stores kinetic energy.

14. Where,
• T is the applied torque
• Tj is the opposing torque due to moment
of inertia
• J is moment of inertia
• α is angular acceleration
• θ is angular displacement

15. Torsional Spring:
• In translational mechanical system,
spring stores potential energy.
• Similarly, in rotational mechanical
system, torsional spring stores
potential energy.
Where,
• T is the applied torque
• Tk is the opposing torque due to
elasticity of torsionalspring
• K is the torsional spring constant
• θ is angular displacement

16. Dashpot
• If a torque is applied on dashpot B, then it
is opposed by an opposing torque due to
the rotational friction of the dashpot.
Where,
• Tb is the opposing torque due to the
rotational friction ofthe
• dashpot
• B is the rotational friction coefficient
• ω is the angular velocity
• θ is the angular displacement

18. Mechanical Translational System
• Consider the following
system

19. • Find the transfer function of th emechanicaltranslationalsystem
given in Figure.

20. • Draw the free body diagram for
the mechanical system

21. Mathematical Model of Electrical System

22. • The following
mathematical models are
mostlyused.
• Differential equation model
• Transfer function model
• State space model
• Example: RLC Circuit
• Mesh equation for this
circuitis

23. • Consider the following electrical system

25. Building up a model for a fluid system
1.For the shown simple
hydraulic system derive an
expression for the height of the
fluid in the container.
Consider the system consist of a
capacitor, the liquid in the
container, with a resistor and a
valve

27. 2.

32. Thermal System building Blocks
• Two basic building blocks: Resistance& capacitance
• The Thermal Resistance:is defined by the relation-
q: rate of heat flow
T2-T1: Temperature difference
R: Thermal resistance
The value of R depends on the mode of heat transfer-
Conduction Mode
K: thermal conductivity of the material through which conductionis taken place
L: length of the material
Convection Mode: in liquid and gasses
A: is the surface area across which there is temperature difference;
h: coefficient of heat transfer

33. • Thermal capacitance: is a measure of the store of internal
energy in a system. It is defined by the following equation
q1-q 2: rate of change of internal energy
C=cm is the thermal capacitance, mis the mass and cis the specific heat capacity

35. Building up a Model for a Thermal system
• Thermometer temperature -T
• Liquid Temperature-TL