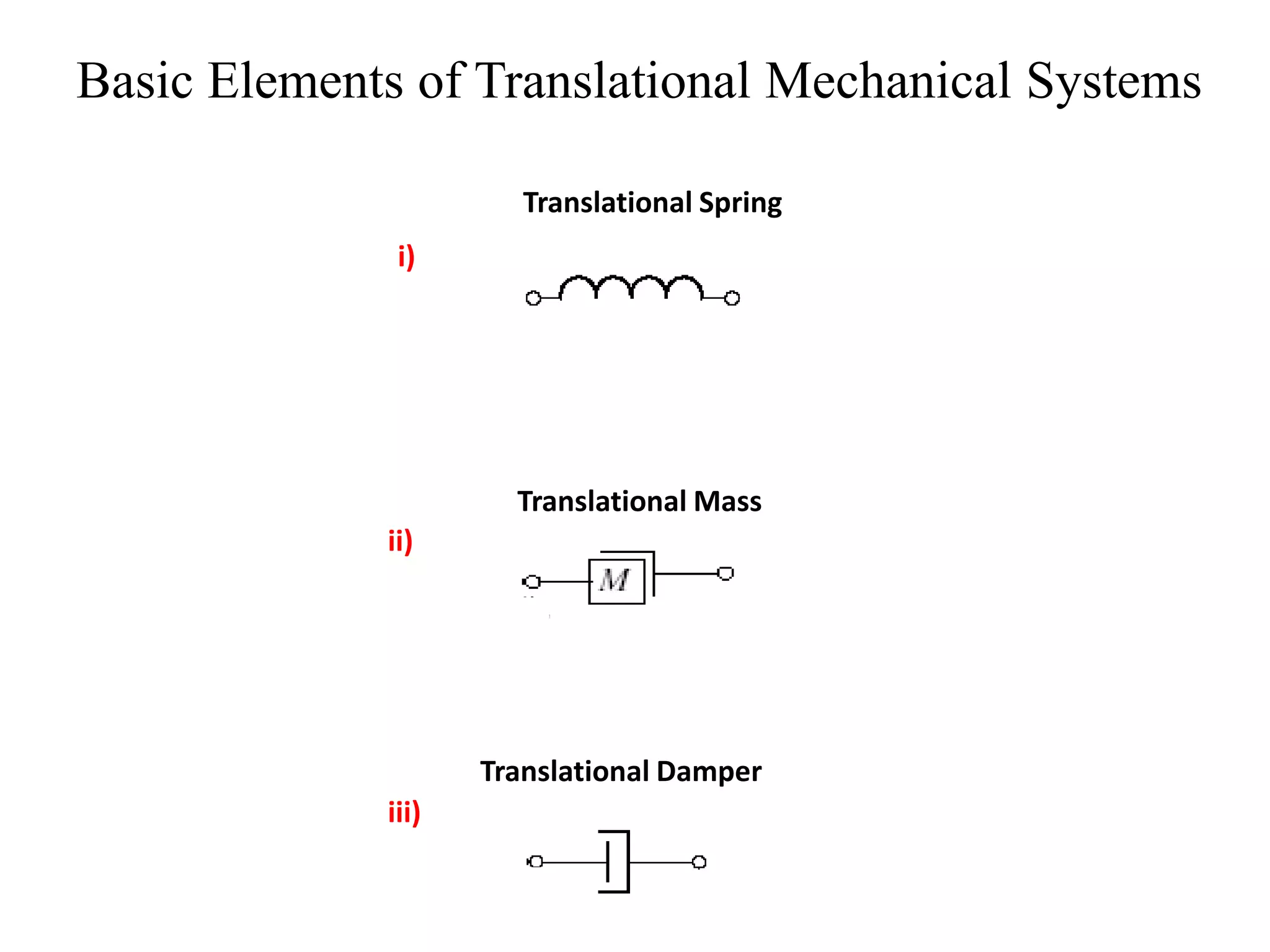
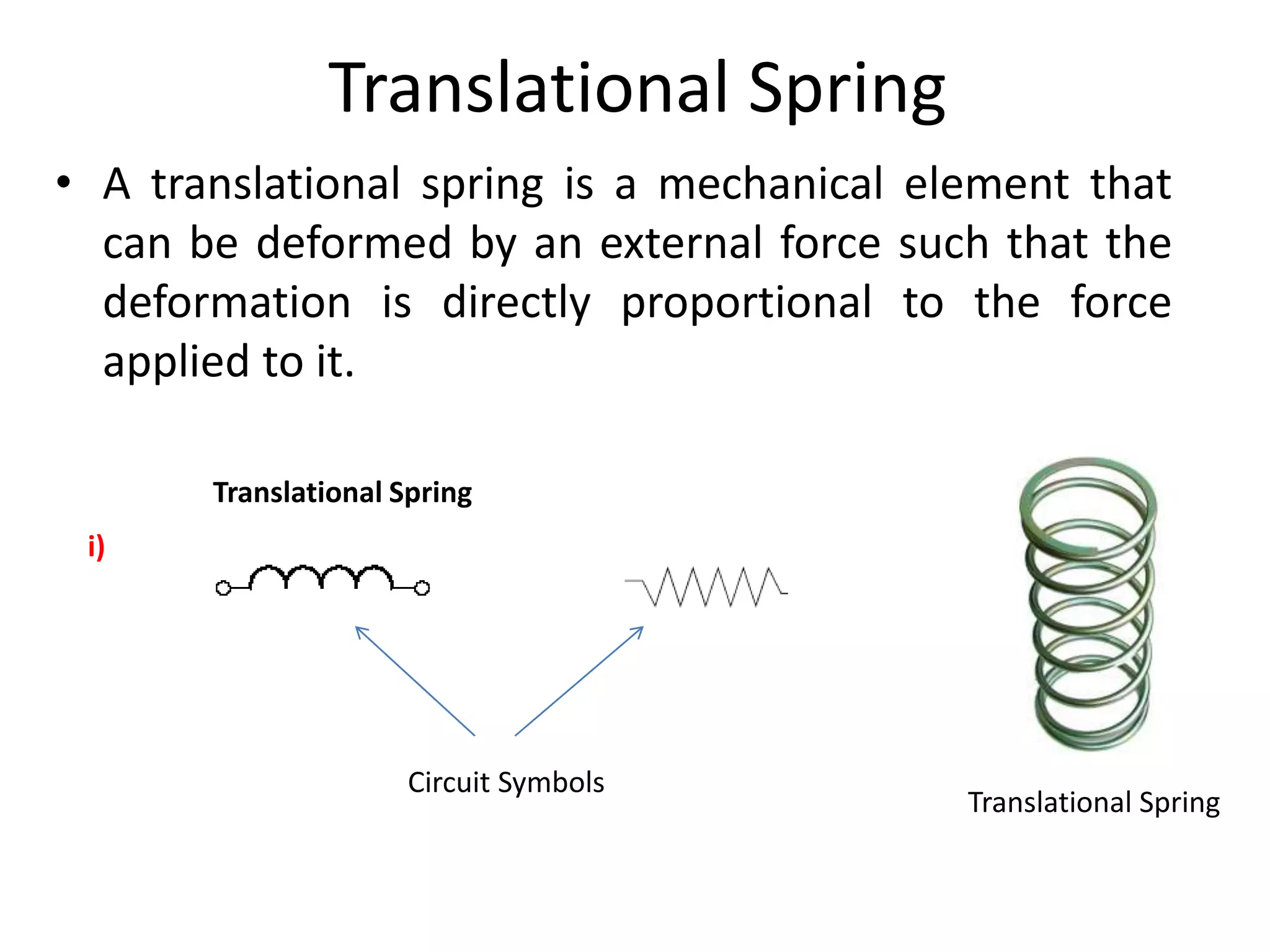
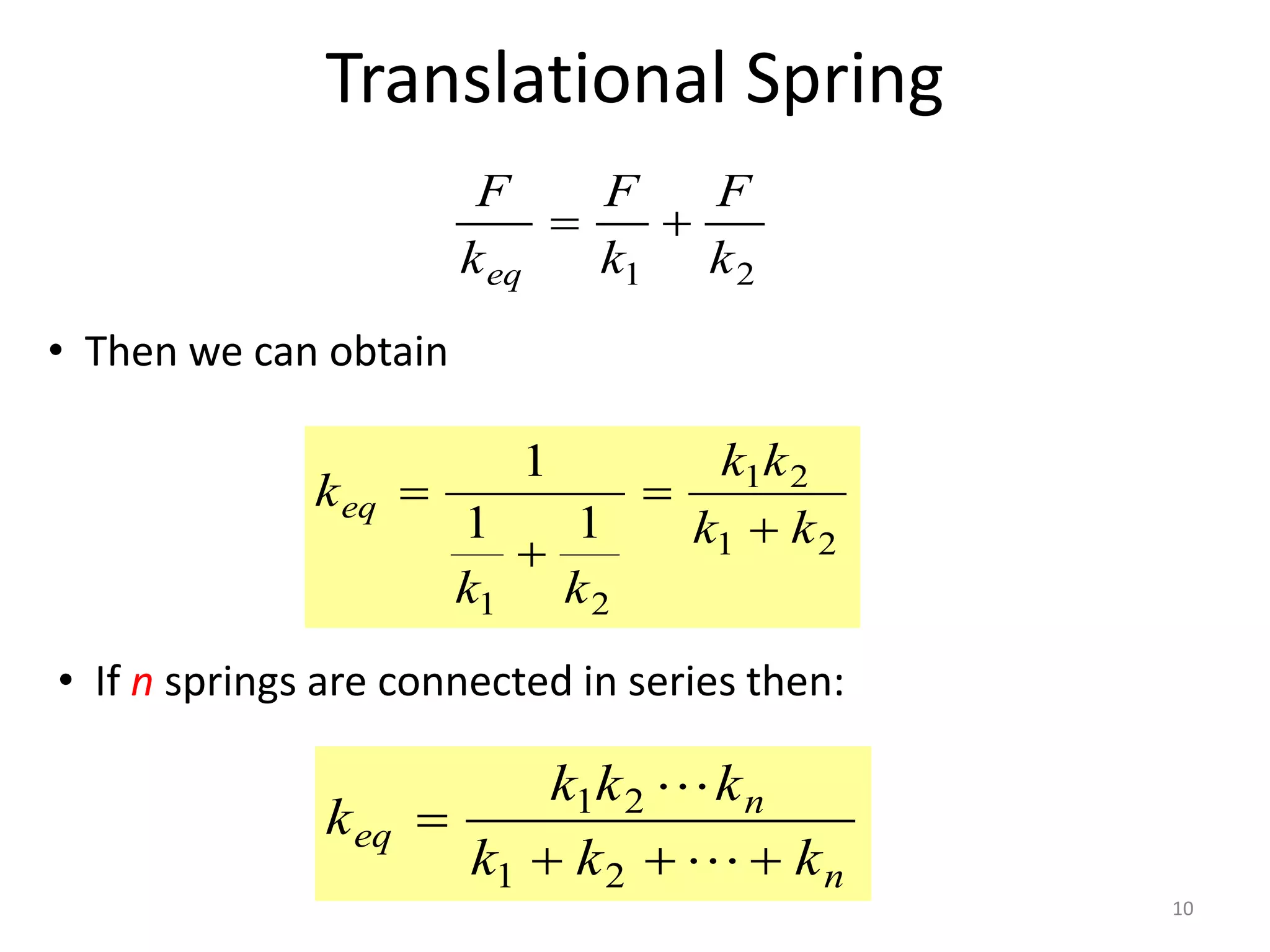
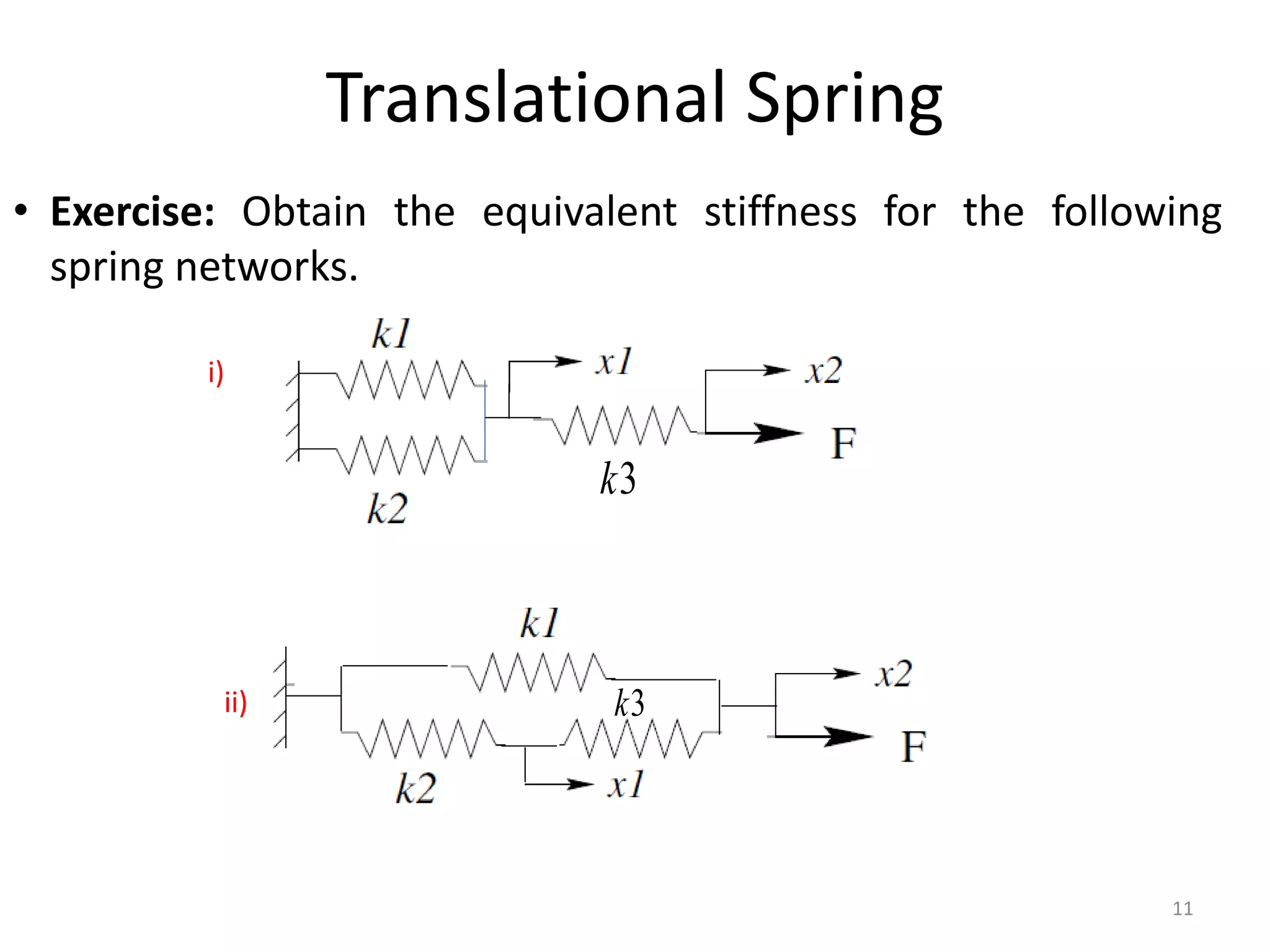
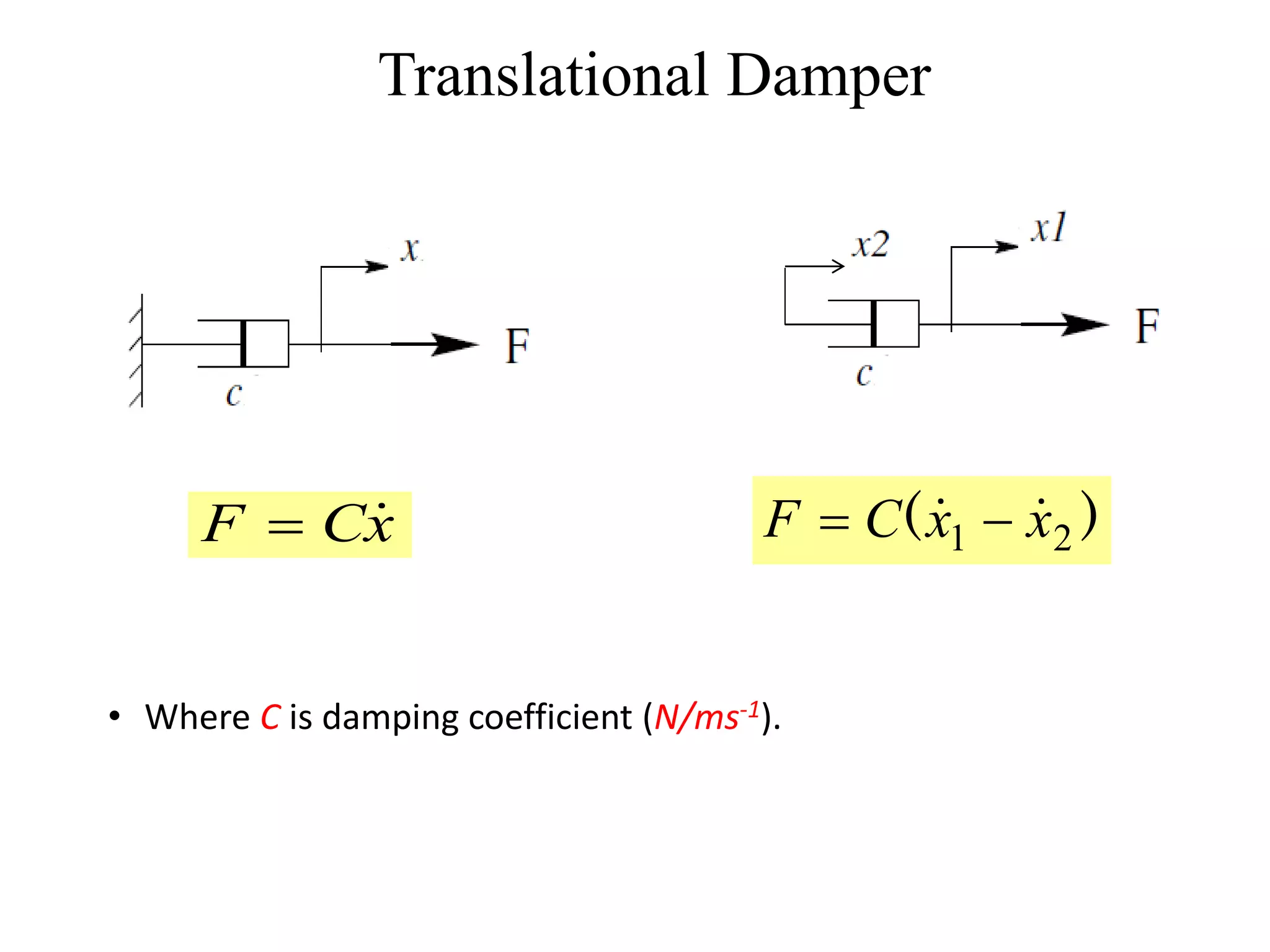
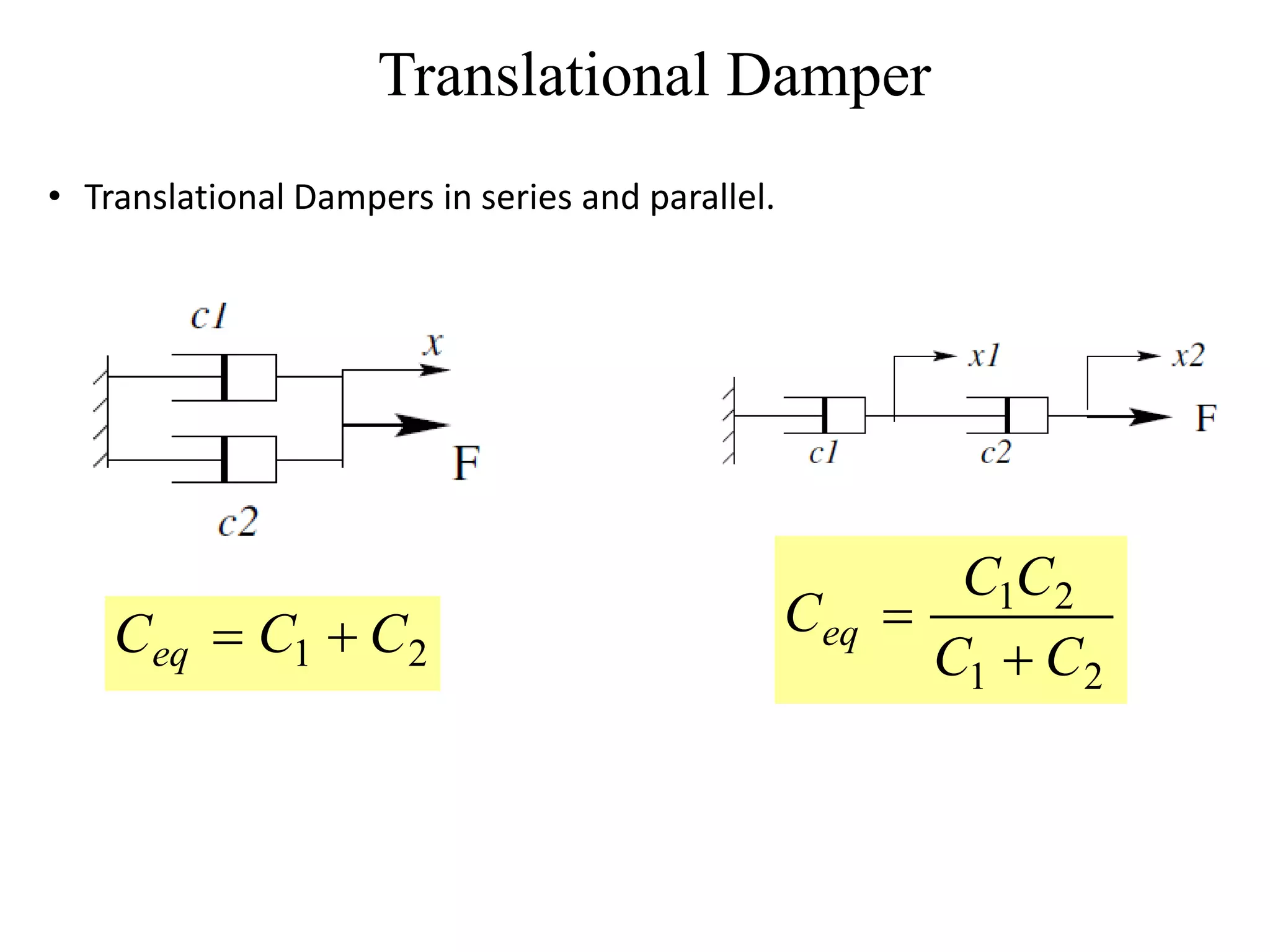
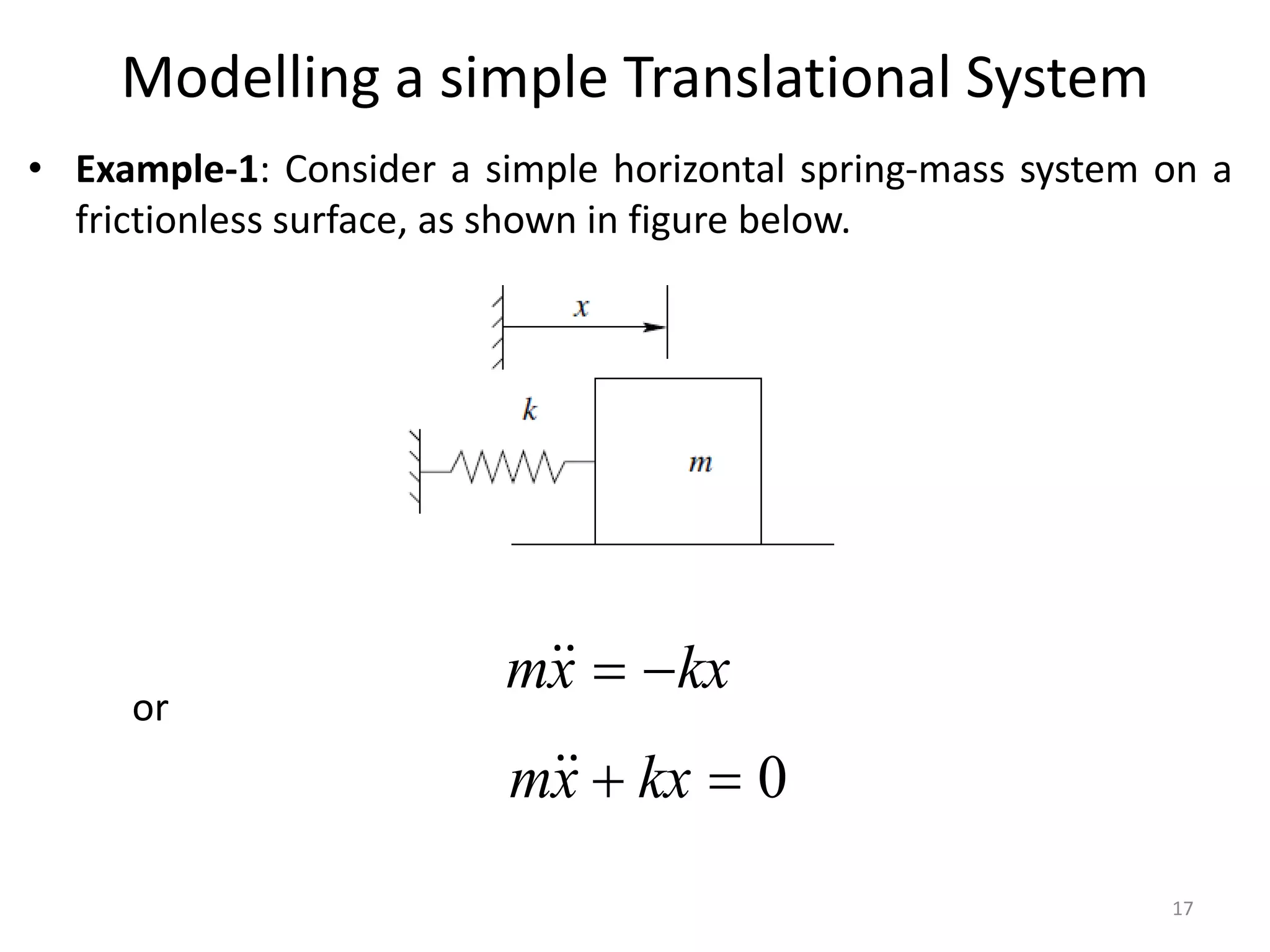
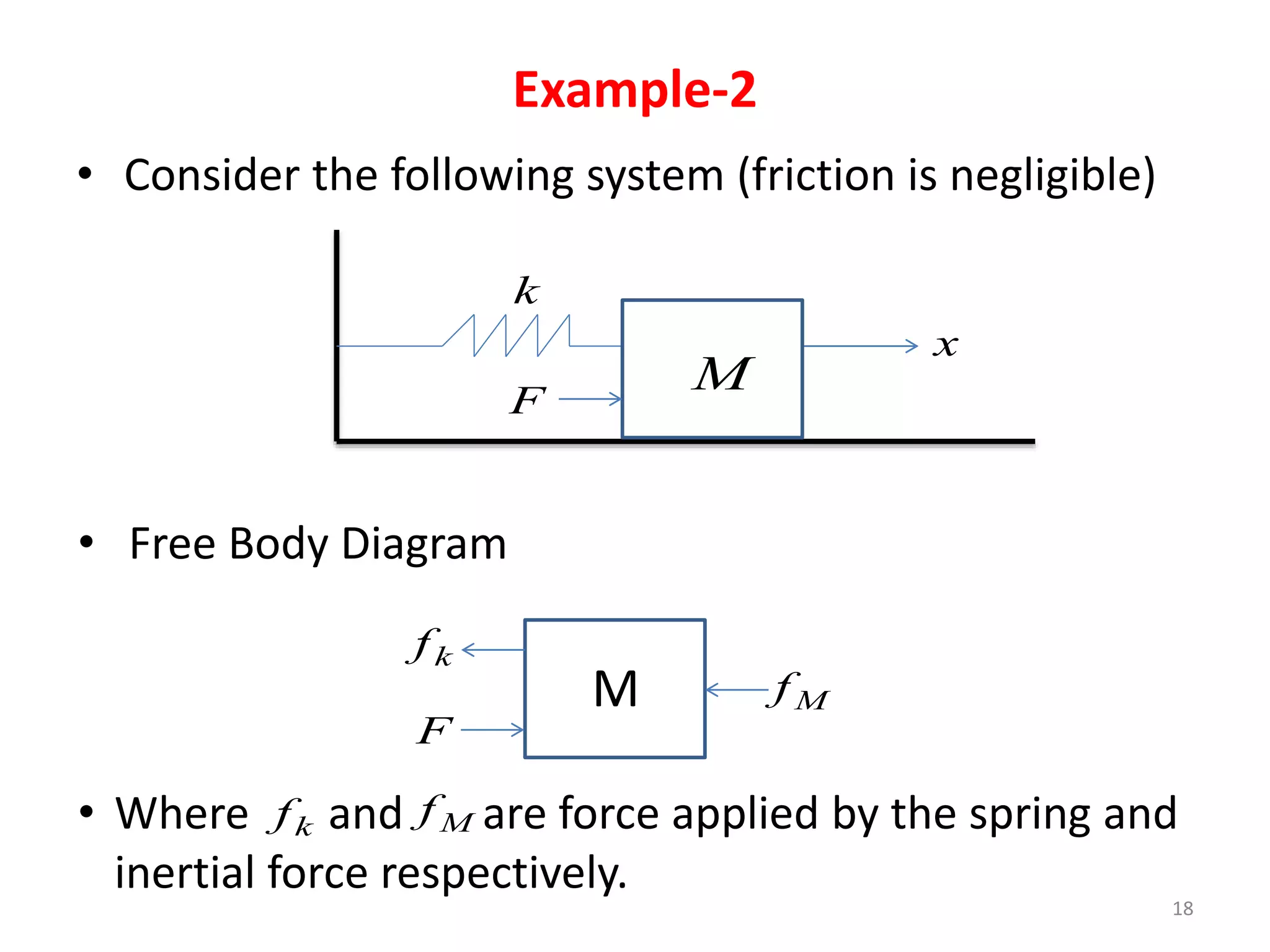
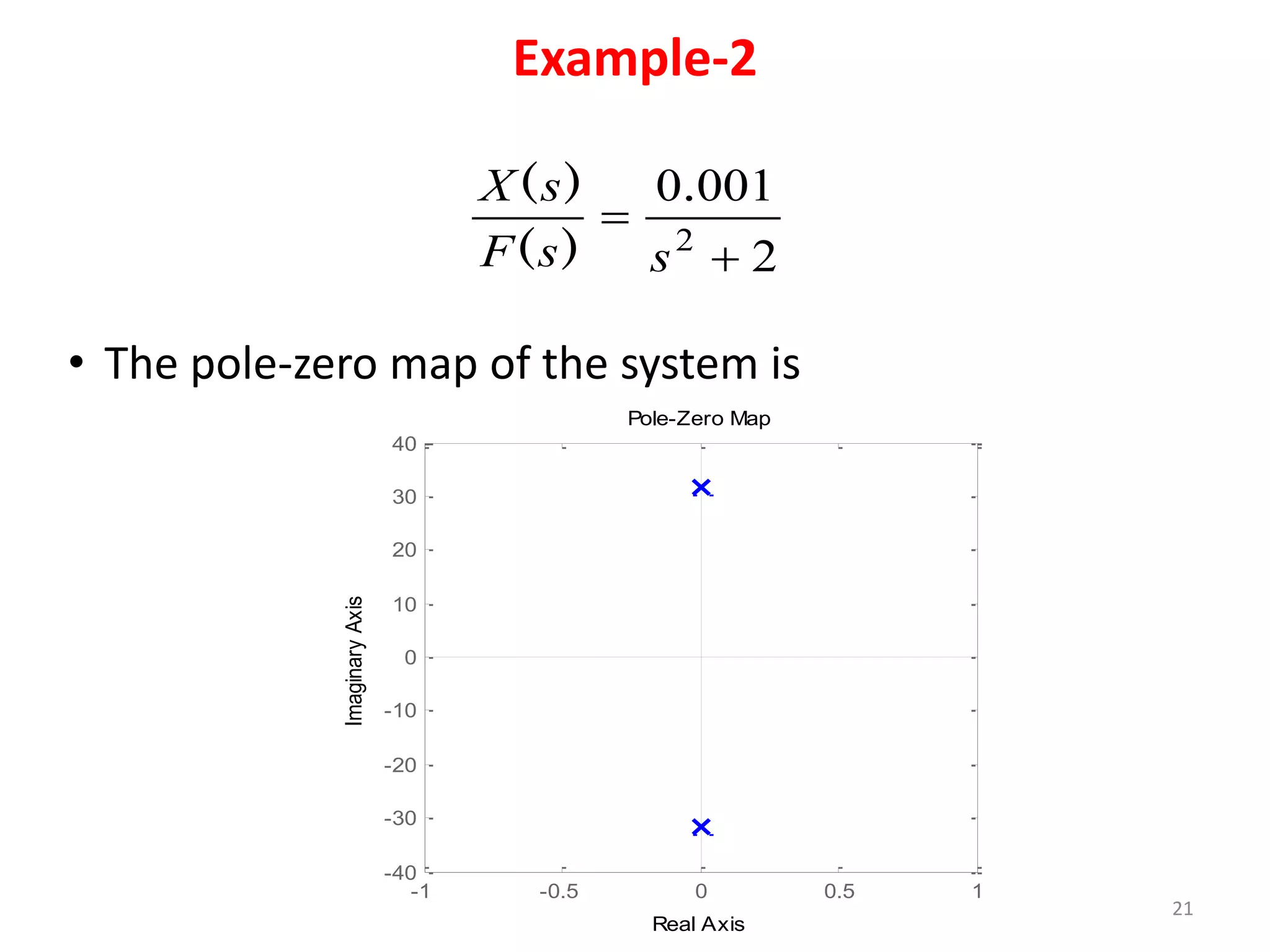
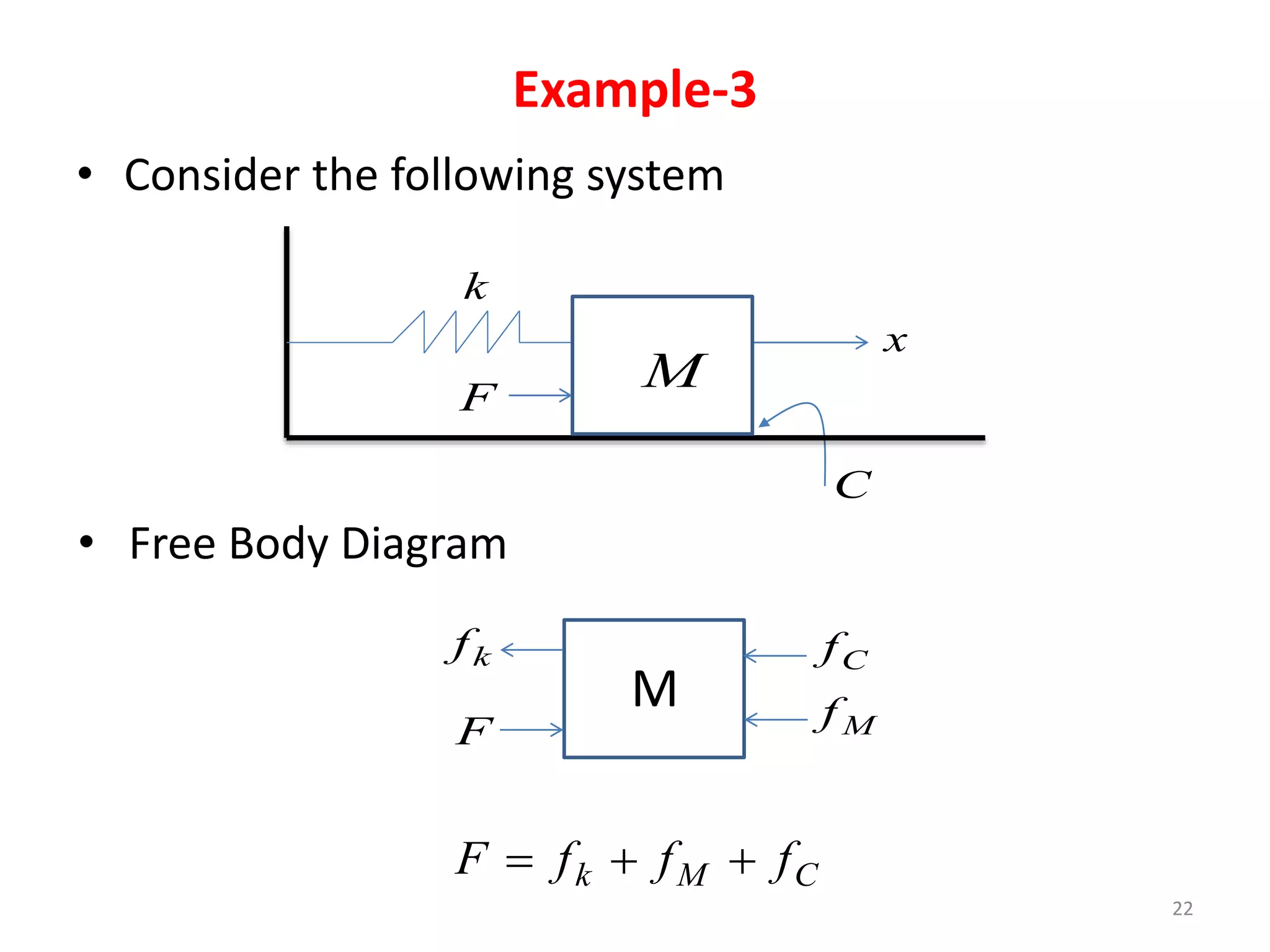
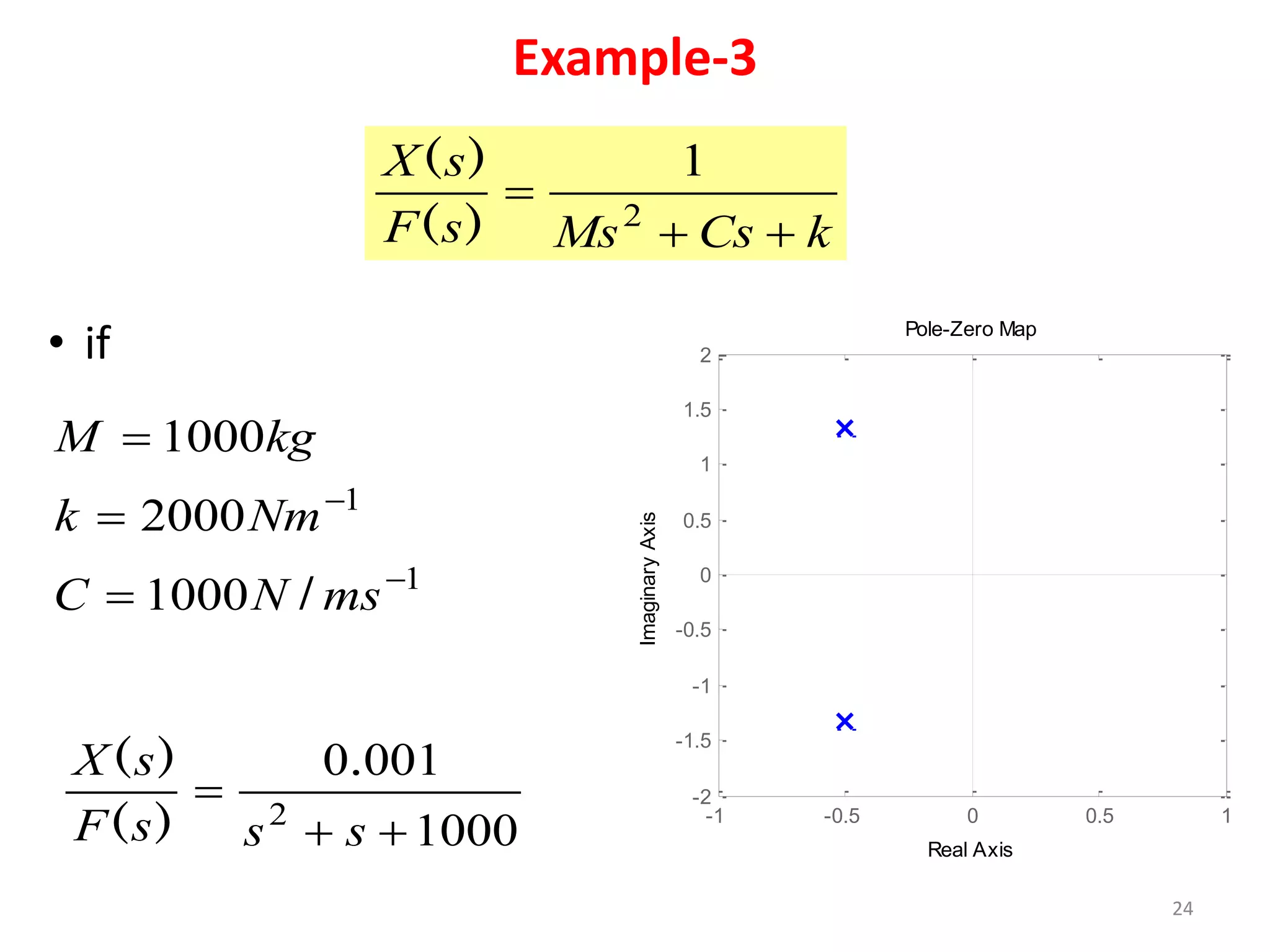
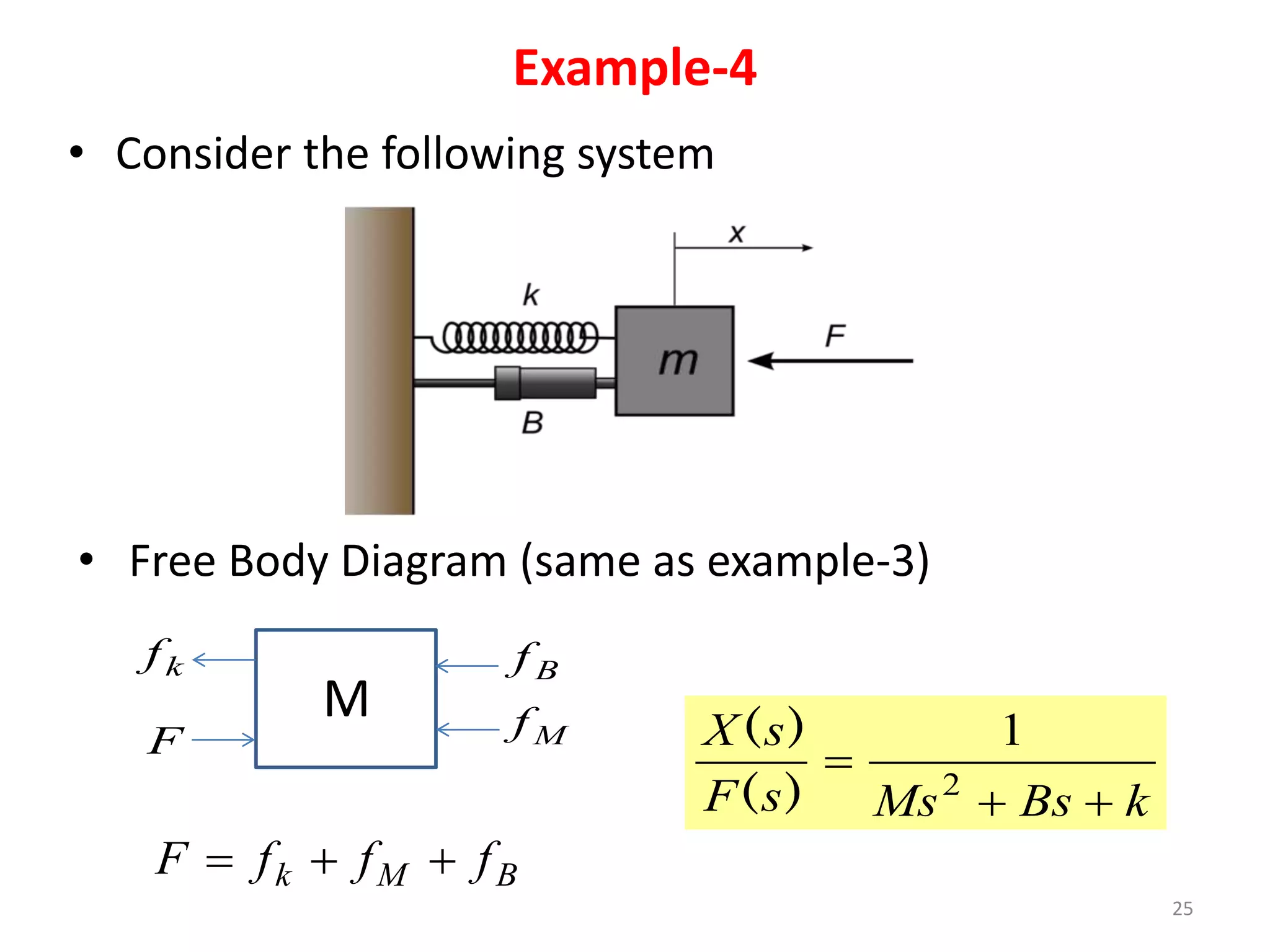
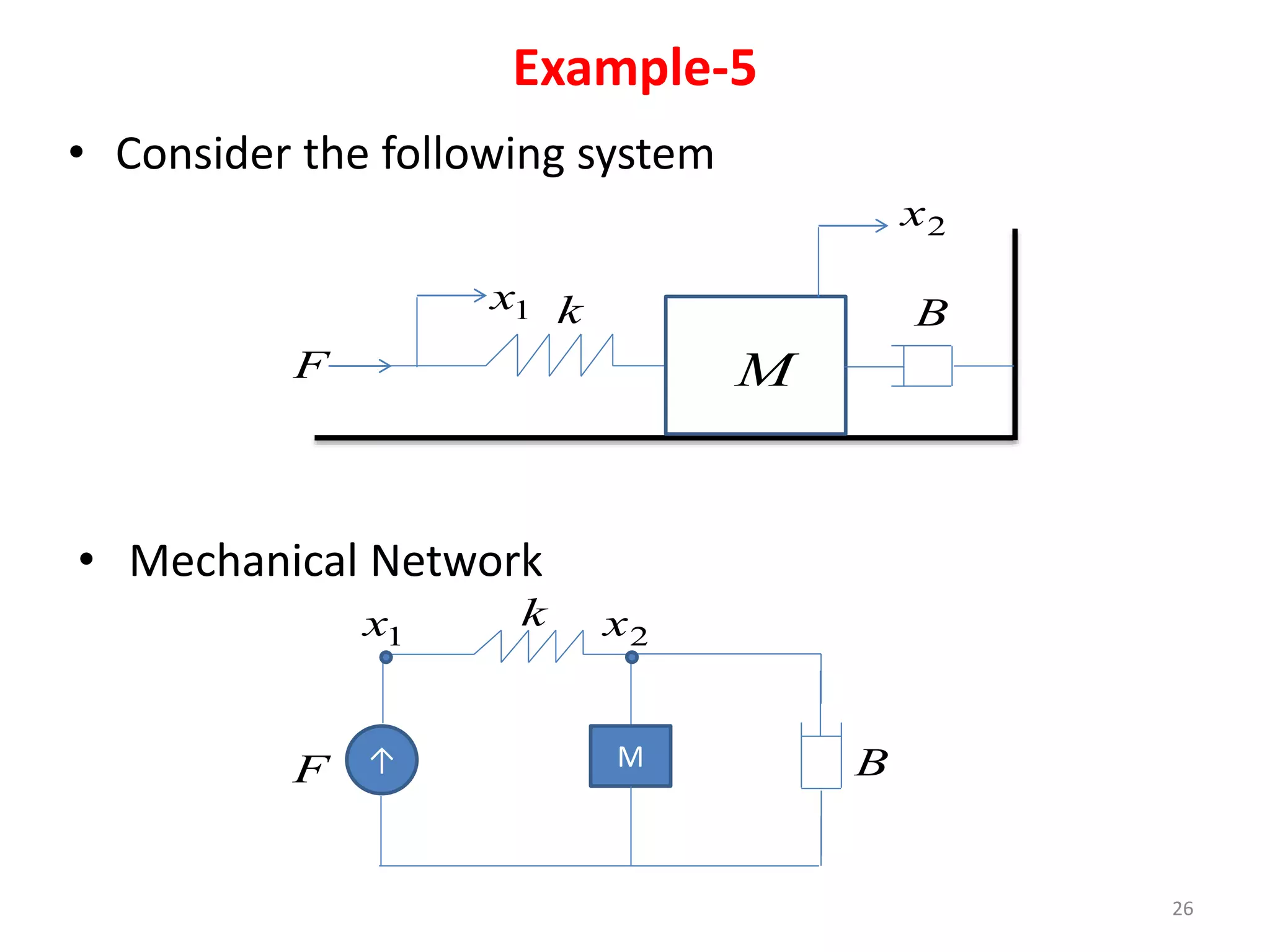
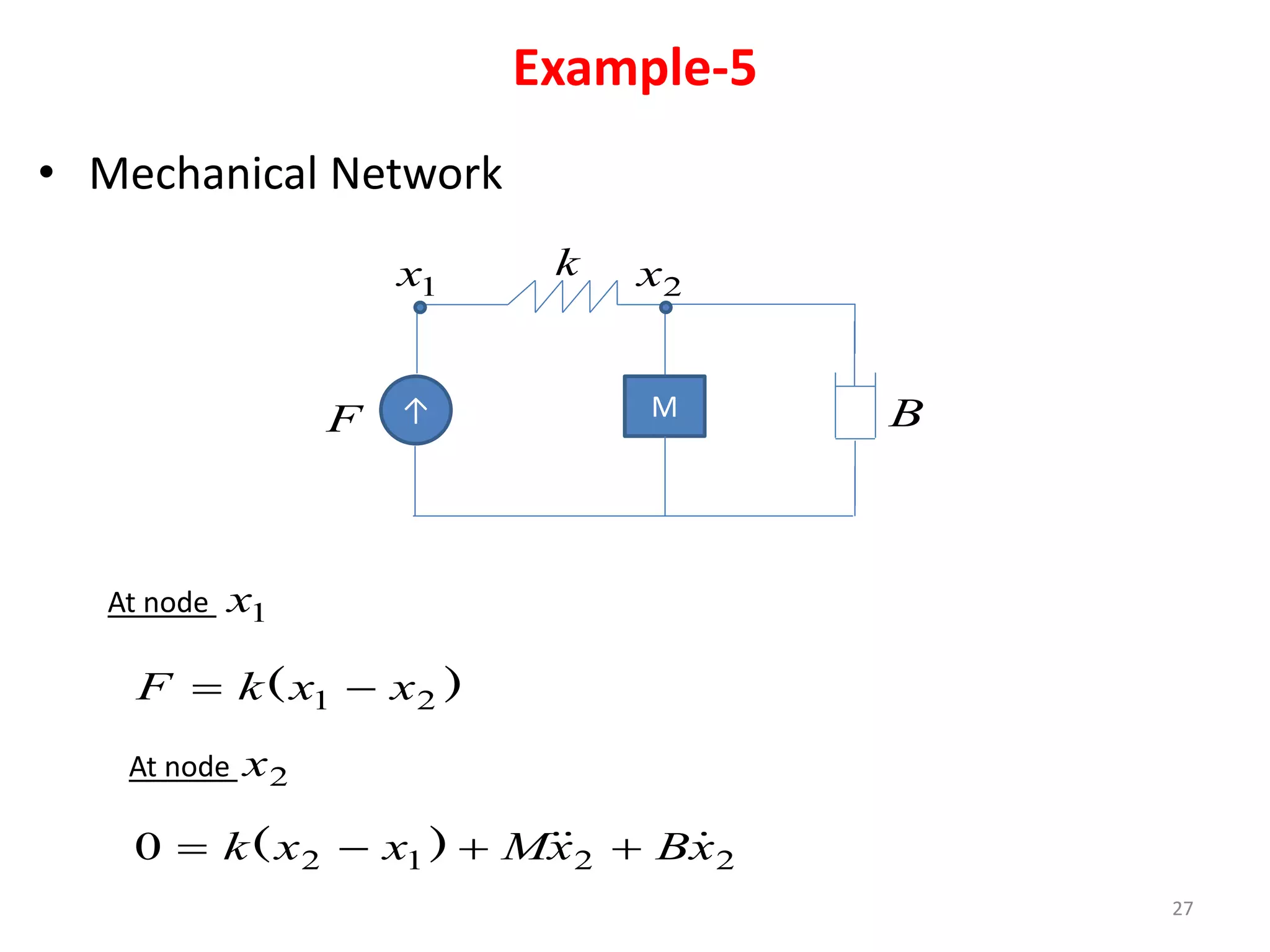
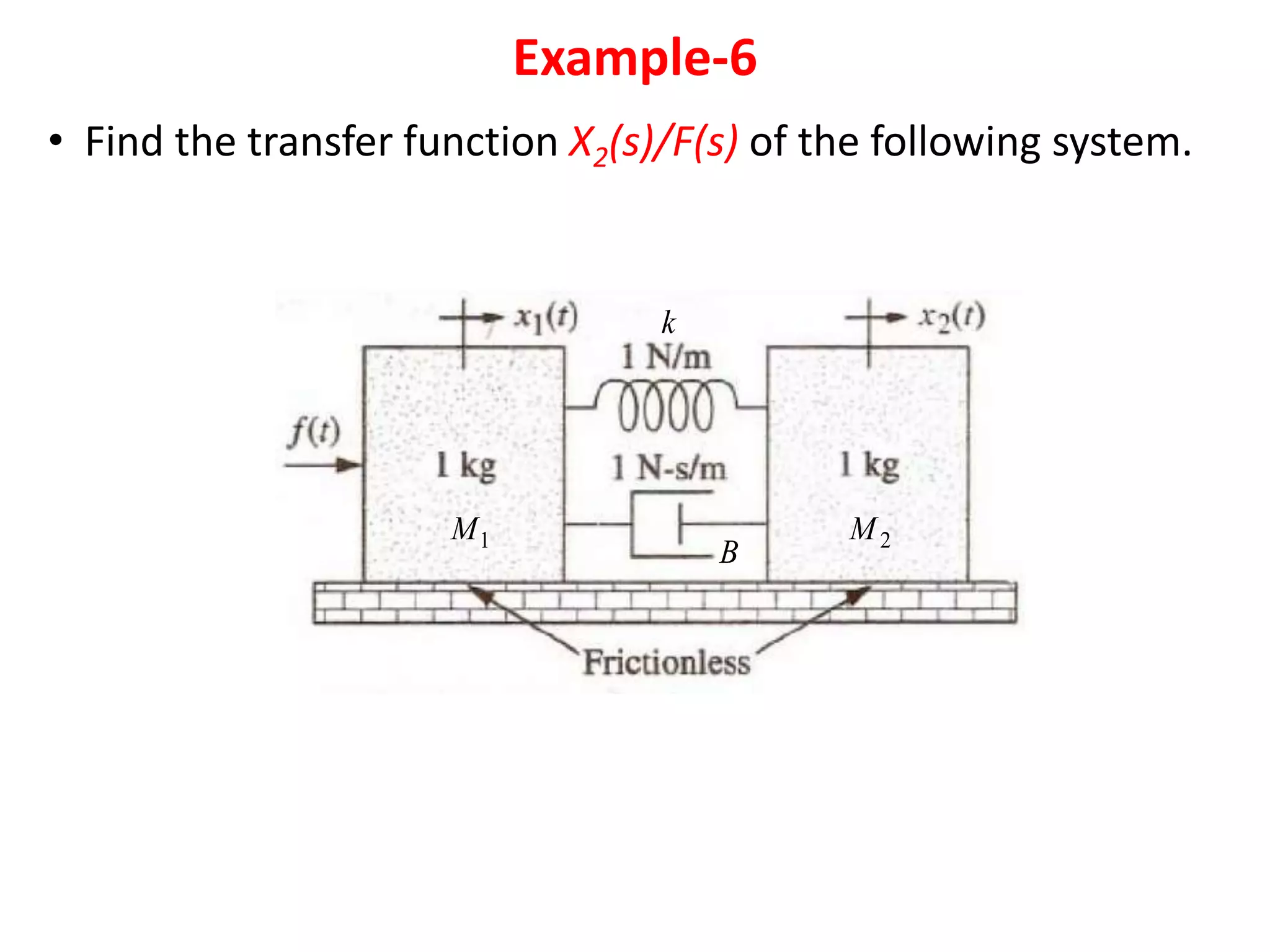
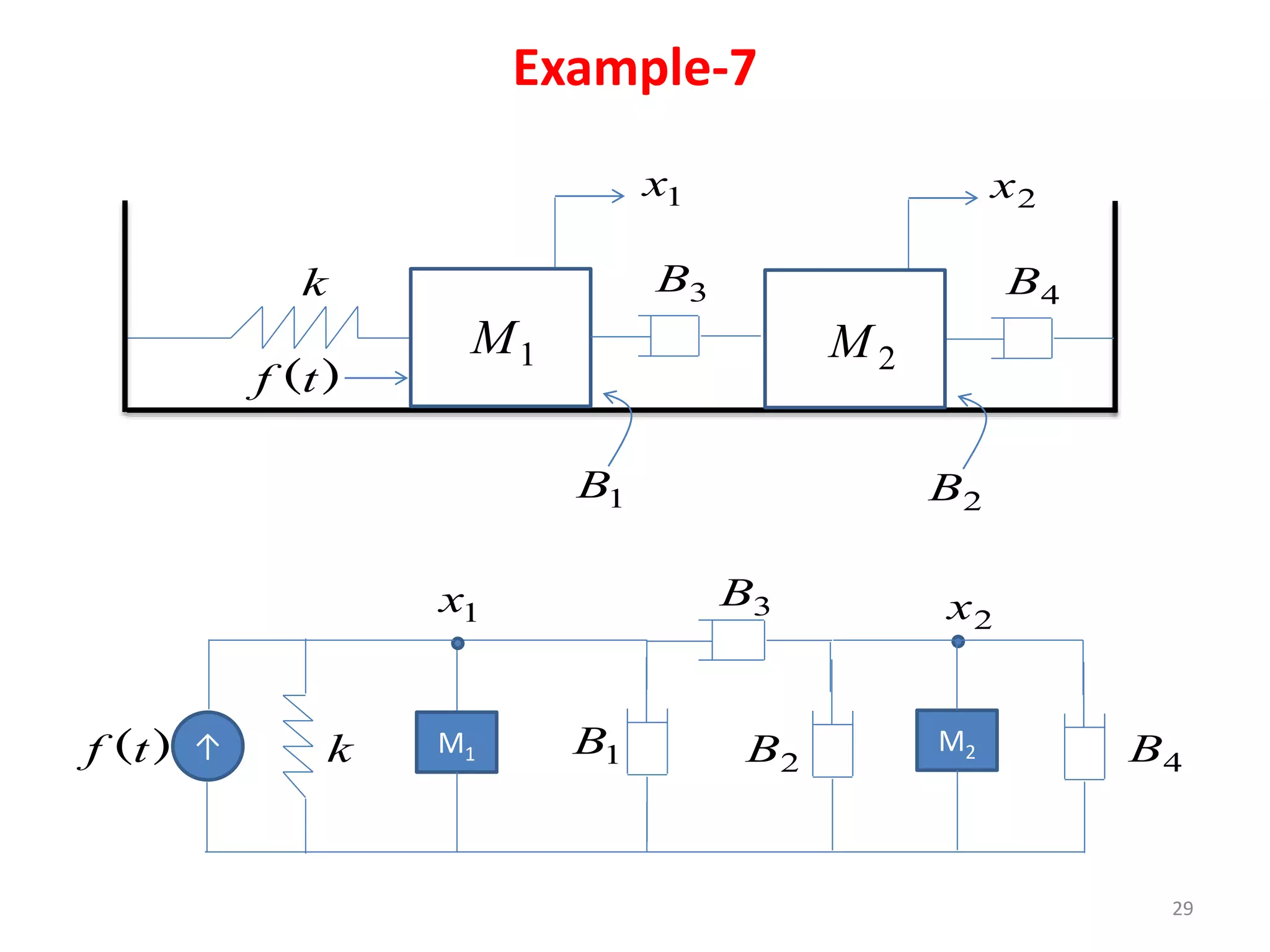
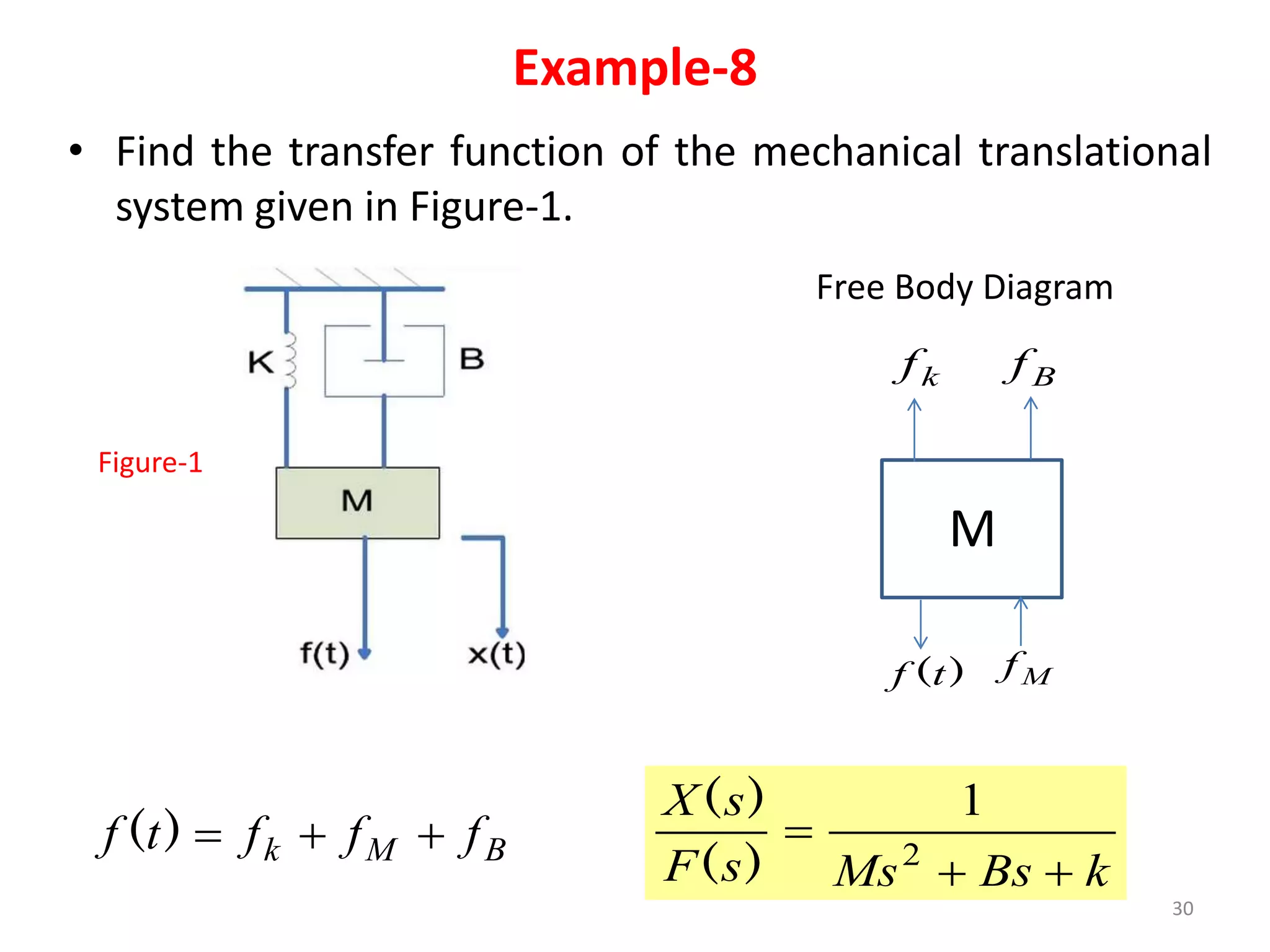
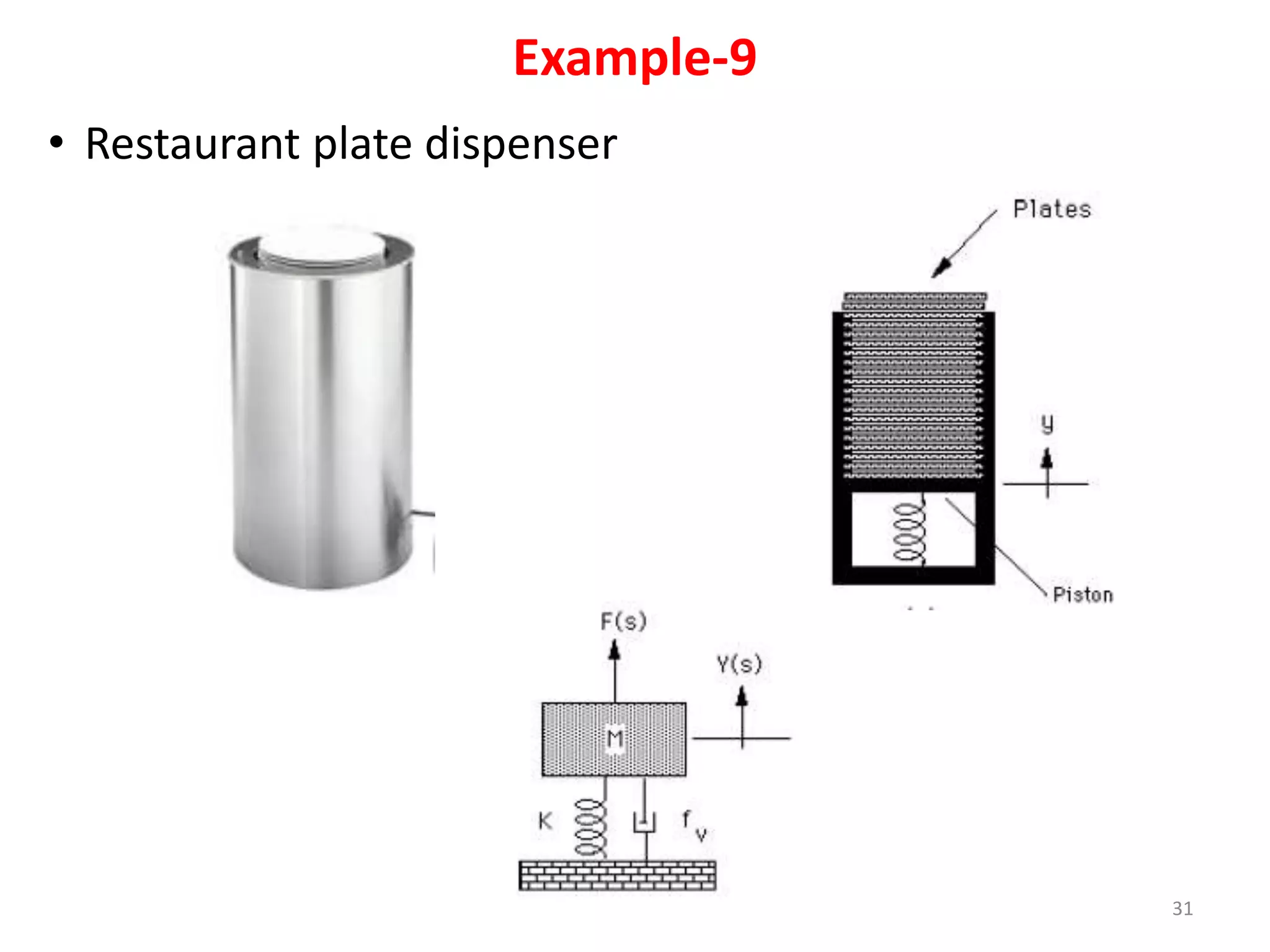
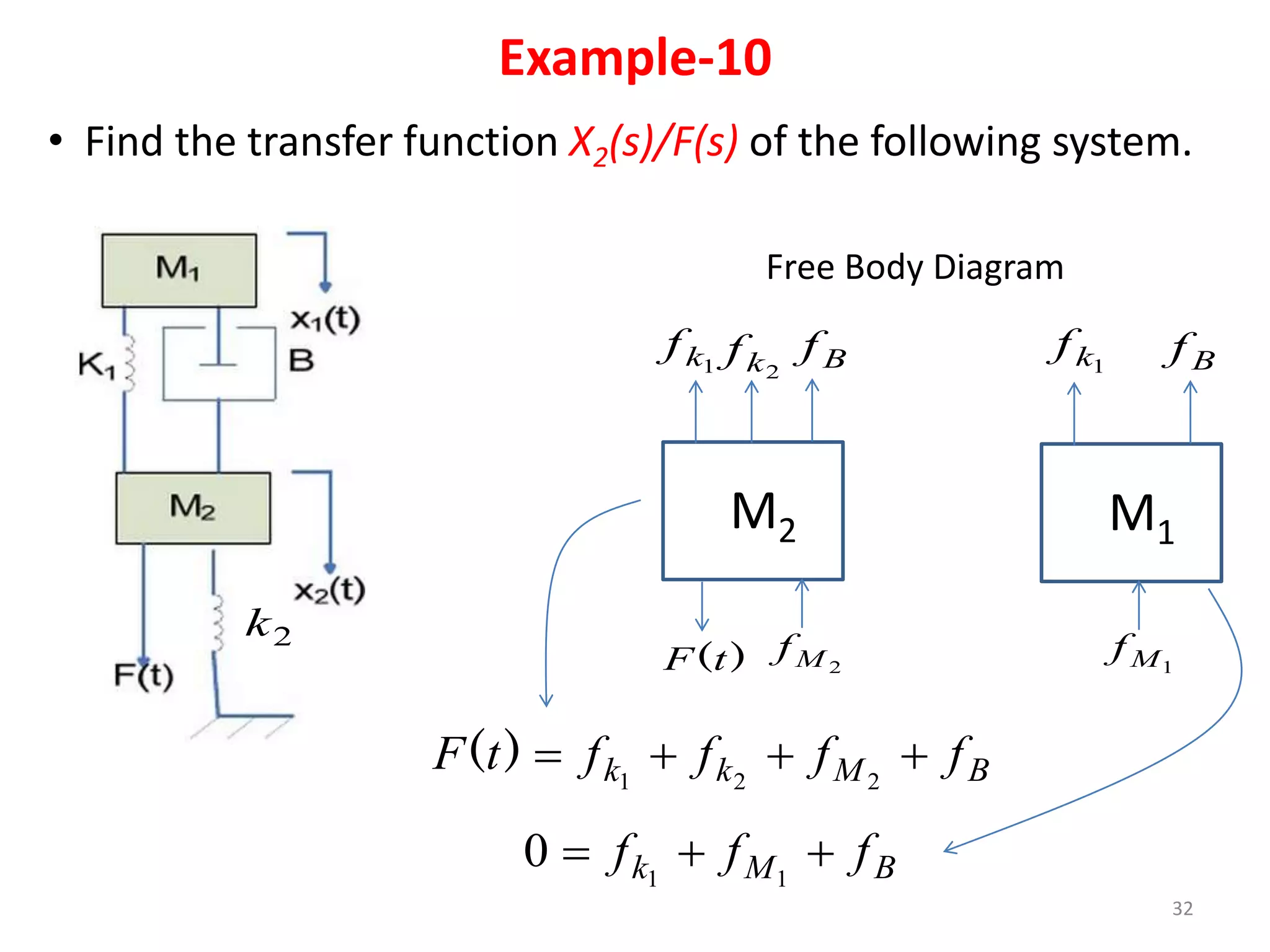
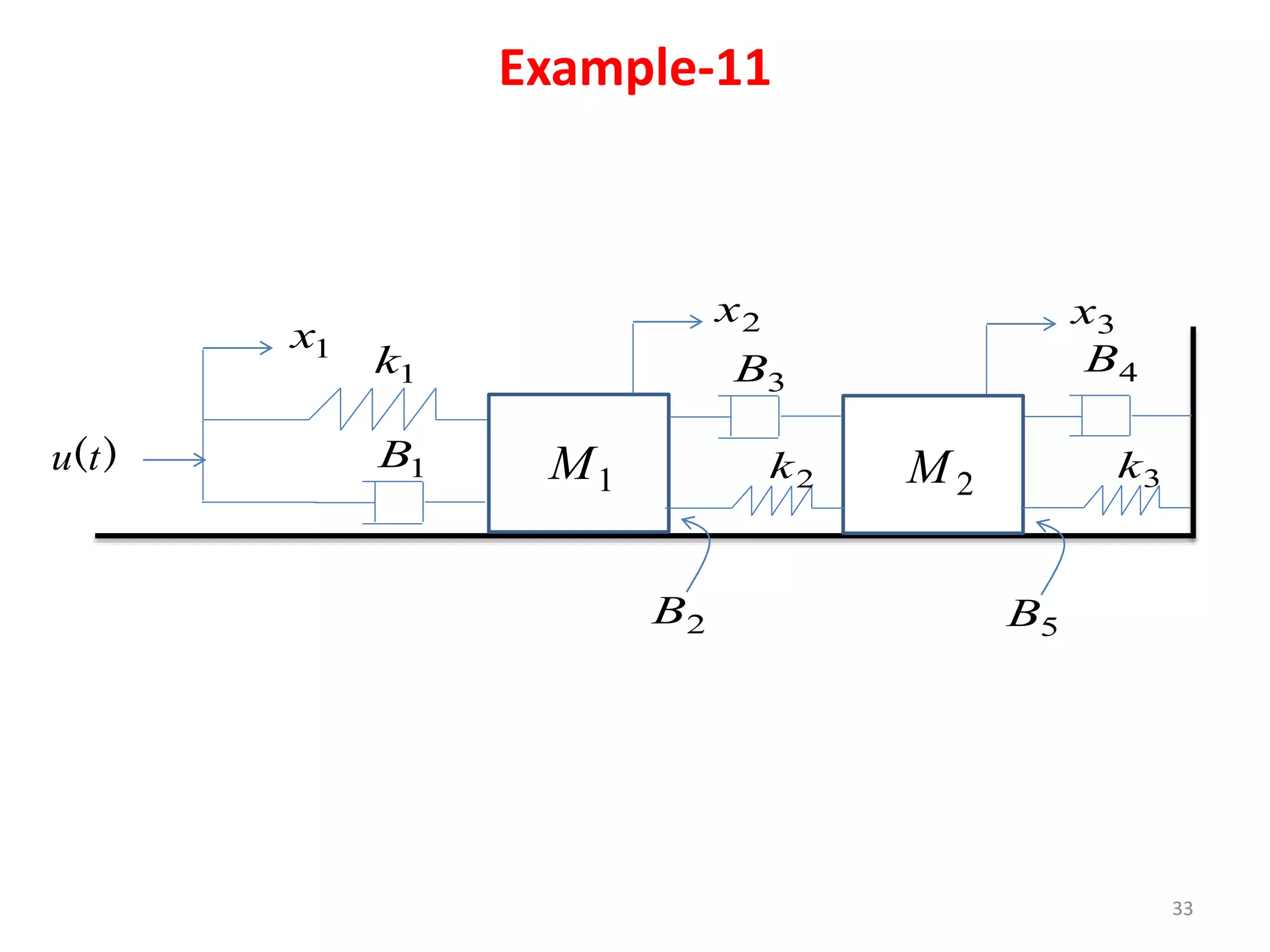
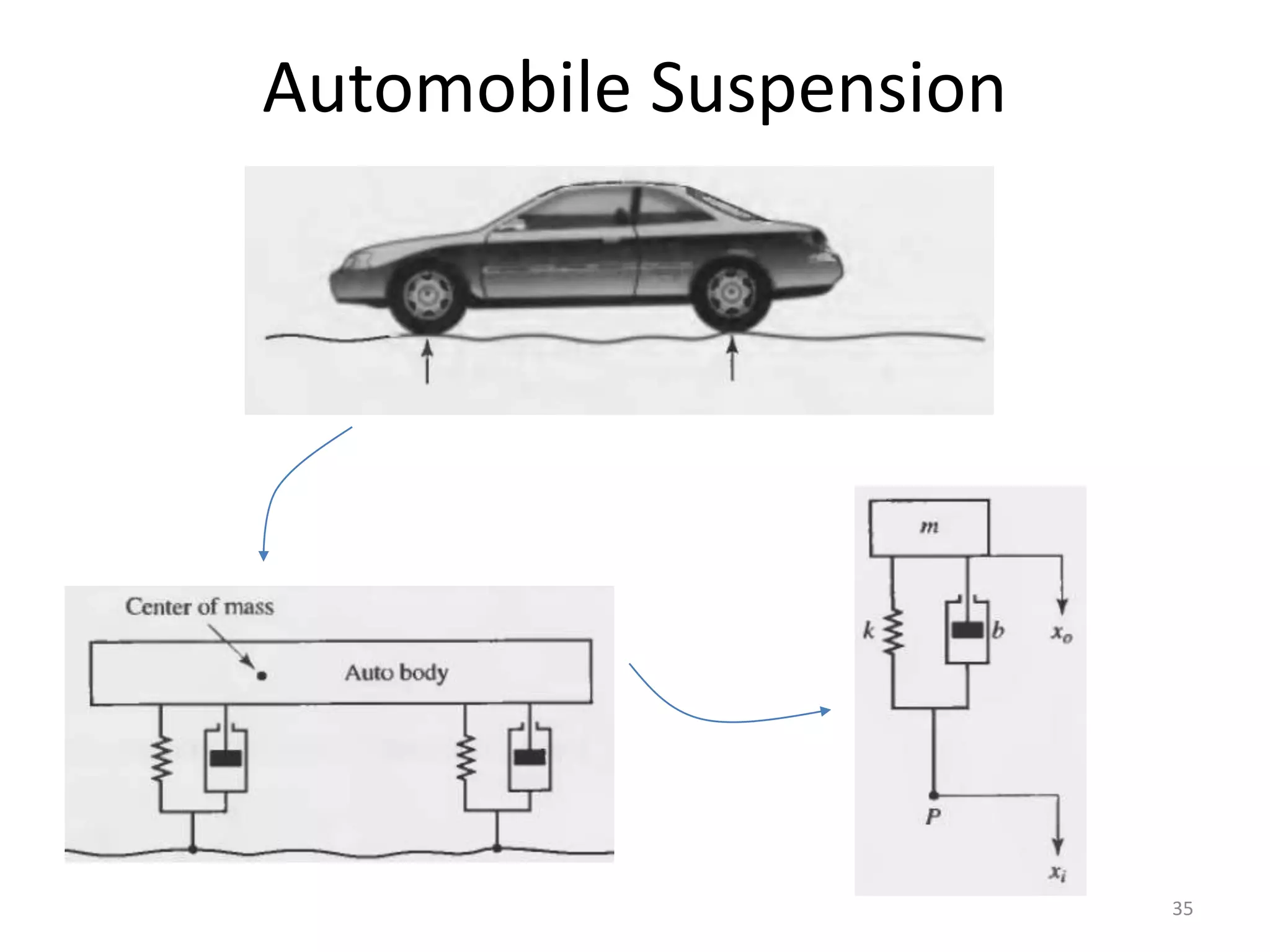
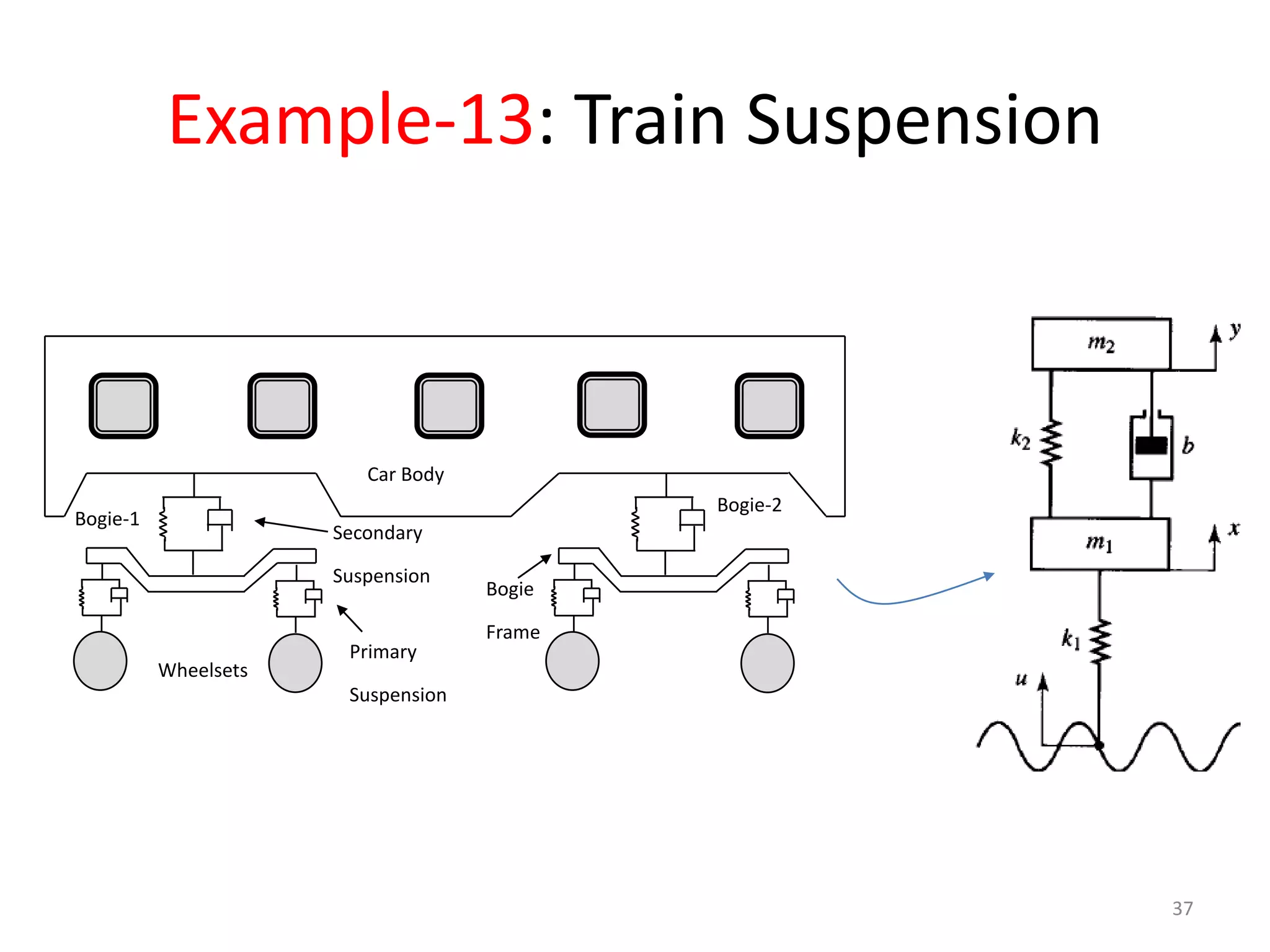
This document provides an outline and overview of translational mechanical systems. It begins by defining translational and rotational mechanical systems. For translational systems, it describes the basic elements of springs, masses, and dampers. It provides examples of modeling simple spring-mass systems and damped systems using differential equations. Applications discussed include automobile and train suspensions. The document aims to introduce the basic concepts and modeling of translational mechanical systems.

1. Outline of this Lecture
• Part-I: Translational Mechanical System
• Part-II: Rotational Mechanical System
• Part-III: Mechanical Linkages
1

2. Basic Types of Mechanical Systems
• Translational
– Linear Motion
• Rotational
– Rotational Motion
2

3. TRANSLATIONAL MECHANICAL SYSTEMS
Part-I
3

4. Basic Elements of Translational Mechanical Systems
Translational Spring
i)
Translational Mass
ii)
Translational Damper
iii)

5. Translational Spring
i)
Circuit Symbols
Translational Spring
• A translational spring is a mechanical element that
can be deformed by an external force such that the
deformation is directly proportional to the force
applied to it.
Translational Spring

6. Translational Spring
• If F is the applied force
• Then is the deformation if
• Or is the deformation.
• The equation of motion is given as
• Where is stiffness of spring expressed in N/m
2
x
1
x
0
2 
x
1
x
)
( 2
1 x
x 
)
( 2
1 x
x
k
F 

k
F
F

7. Translational Spring
• Given two springs with spring constant k1 and k2, obtain
the equivalent spring constant keq for the two springs
connected in:
7
(1) Parallel (2) Series

8. Translational Spring
8
(1) Parallel
F
x
k
x
k 
 2
1
F
x
k
k 
 )
( 2
1
F
x
keq 
• The two springs have same displacement therefore:
2
1 k
k
keq 

• If n springs are connected in parallel then:
n
eq k
k
k
k 


 
2
1

9. Translational Spring
9
(2) Series
F
x
k
x
k 
 2
2
1
1
• The forces on two springs are same, F, however
displacements are different therefore:
1
1
k
F
x 
2
2
k
F
x 
• Since the total displacement is , and we have
2
1 x
x
x 
 x
k
F eq

2
1
2
1
k
F
k
F
k
F
x
x
x
eq






10. Translational Spring
10
• Then we can obtain
2
1
2
1
2
1
1
1
1
k
k
k
k
k
k
keq




2
1 k
F
k
F
k
F
eq


• If n springs are connected in series then:
n
n
eq
k
k
k
k
k
k
k






2
1
2
1

11. Translational Spring
11
• Exercise: Obtain the equivalent stiffness for the following
spring networks.
3
k
i)
ii) 3
k

12. Translational Mass
Translational Mass
ii)
• Translational Mass is an inertia
element.
• A mechanical system without
mass does not exist.
• If a force F is applied to a mass
and it is displaced to x meters
then the relation b/w force and
displacements is given by
Newton’s law.
M
)
(t
F
)
(t
x
x
M
F 



13. Translational Damper
Translational Damper
iii)
• When the viscosity or drag is not
negligible in a system, we often
model them with the damping
force.
• All the materials exhibit the
property of damping to some
extent.
• If damping in the system is not
enough then extra elements (e.g.
Dashpot) are added to increase
damping.

14. Common Uses of Dashpots
Door Stoppers
Vehicle Suspension
Bridge Suspension
Flyover Suspension

15. Translational Damper
x
C
F 

• Where C is damping coefficient (N/ms-1).
)
( 2
1 x
x
C
F 
 


16. Translational Damper
• Translational Dampers in series and parallel.
2
1 C
C
Ceq 

2
1
2
1
C
C
C
C
Ceq



17. Modelling a simple Translational System
• Example-1: Consider a simple horizontal spring-mass system on a
frictionless surface, as shown in figure below.
or
17
kx
x
m 



0

 kx
x
m 


18. Example-2
• Consider the following system (friction is negligible)
18
• Free Body Diagram
M
F
k
f
M
f
k
F
x
M
• Where and are force applied by the spring and
inertial force respectively.
k
f M
f

19. Example-2
19
• Then the differential equation of the system is:
kx
x
M
F 
 

• Taking the Laplace Transform of both sides and ignoring
initial conditions we get
M
F
k
f
M
f
M
k f
f
F 

)
(
)
(
)
( s
kX
s
X
Ms
s
F 
 2

20. 20
)
(
)
(
)
( s
kX
s
X
Ms
s
F 
 2
• The transfer function of the system is
k
Ms
s
F
s
X

 2
1
)
(
)
(
• if
1
2000
1000



Nm
k
kg
M
2
001
0
2


s
s
F
s
X .
)
(
)
(
Example-2

21. 21
• The pole-zero map of the system is
2
001
0
2


s
s
F
s
X .
)
(
)
(
Example-2
-1 -0.5 0 0.5 1
-40
-30
-20
-10
0
10
20
30
40
Pole-Zero Map
Real Axis
Imaginary
Axis

22. Example-3
• Consider the following system
22
• Free Body Diagram
k
F
x
M
C
M
F
k
f
M
f
C
f
C
M
k f
f
f
F 



23. Example-3
23
Differential equation of the system is:
kx
x
C
x
M
F 

 


Taking the Laplace Transform of both sides and ignoring
Initial conditions we get
)
(
)
(
)
(
)
( s
kX
s
CsX
s
X
Ms
s
F 

 2
k
Cs
Ms
s
F
s
X


 2
1
)
(
)
(

24. Example-3
24
k
Cs
Ms
s
F
s
X


 2
1
)
(
)
(
• if
1
1
1000
2000
1000





ms
N
C
Nm
k
kg
M
/
1000
001
0
2



s
s
s
F
s
X .
)
(
)
(
-1 -0.5 0 0.5 1
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
Pole-Zero Map
Real Axis
Imaginary
Axis

25. Example-4
• Consider the following system
25
• Free Body Diagram (same as example-3)
M
F
k
f
M
f
B
f
B
M
k f
f
f
F 


k
Bs
Ms
s
F
s
X


 2
1
)
(
)
(

26. Example-5
• Consider the following system
26
• Mechanical Network
k
F
2
x
M
1
x B
↑ M
k
B
F
1
x 2
x

27. Example-5
27
• Mechanical Network
↑ M
k
B
F
1
x 2
x
)
( 2
1 x
x
k
F 

At node 1
x
At node 2
x
2
2
1
2
0 x
B
x
M
x
x
k 

 


 )
(

28. Example-6
• Find the transfer function X2(s)/F(s) of the following system.
1
M 2
M
k
B

29. Example-7
29
k
)
(t
f
2
x
1
M
4
B
3
B
2
M
1
x
1
B 2
B
↑ M1
k 1
B
)
(t
f
1
x 2
x
3
B
2
B M2
4
B

30. Example-8
• Find the transfer function of the mechanical translational
system given in Figure-1.
30
Free Body Diagram
Figure-1
M
)
(t
f
k
f
M
f
B
f
B
M
k f
f
f
t
f 


)
(
k
Bs
Ms
s
F
s
X


 2
1
)
(
)
(

31. Example-9
31
• Restaurant plate dispenser

32. Example-10
32
• Find the transfer function X2(s)/F(s) of the following system.
Free Body Diagram
M1
1
k
f
1
M
f
B
f
M2
)
(t
F
1
k
f
2
M
f
B
f
2
k
f
2
k
B
M
k
k f
f
f
f
t
F 


 2
2
1
)
(
B
M
k f
f
f 

 1
1
0

33. Example-11
33
1
k
)
(t
u
3
x
1
M
4
B
3
B
2
M
2
x
2
B 5
B
2
k 3
k
1
x
1
B

34. Example-12: Automobile Suspension
34

35. Automobile Suspension
35

36. Automobile Suspension
36
)
.
(
)
(
)
( 1
0 eq




 i
o
i
o
o x
x
k
x
x
b
x
m 



2
eq.
i
i
o
o
o kx
x
b
kx
x
b
x
m 


 



Taking Laplace Transform of the equation (2)
)
(
)
(
)
(
)
(
)
( s
kX
s
bsX
s
kX
s
bsX
s
X
ms i
i
o
o
o 



2
k
bs
ms
k
bs
s
X
s
X
i
o



 2
)
(
)
(

37. Example-13: Train Suspension
37
Car Body
Bogie-2
Bogie
Frame
Bogie-1
Wheelsets
Primary
Suspension
Secondary
Suspension

38. Example: Train Suspension
38