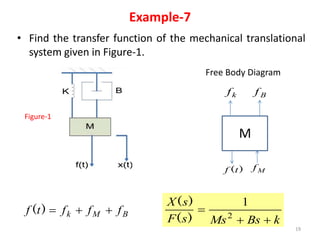
1. The document discusses basic elements of mechanical systems including translational springs, masses, and dampers as well as rotational springs, dampers, and moments of inertia. It provides the equations of motion for each element. 2. Examples are presented of mechanical systems modeled as combinations of springs, masses, and dampers. The differential equations of motion are developed and transfer functions derived for each example system. 3. Rotational systems with springs, dampers, and moments of inertia are also modeled as examples. Circuit diagrams illustrate combinations of rotational elements and the corresponding differential equations are determined.

1. MATHEMATICAL MODELING OF
MECHANICAL SYSTEMS
1

2. Basic Types of Mechanical Systems
• Translational
– Linear Motion
• Rotational
– Rotational Motion
2

3. Basic Elements of Translational Mechanical Systems
Translational Spring
i)
Translational Mass
ii)
Translational Damper
iii)

4. Translational Spring
i)
Circuit Symbols
Translational Spring
• A translational spring is a mechanical element that
can be deformed by an external force such that the
deformation is directly proportional to the force
applied to it.
Translational Spring

5. Translational Spring
• If F is the applied force
• Then is the deformation if
• Or is the deformation.
• The equation of motion is given as
• Where is stiffness of spring expressed in N/m
2
x
1
x
0
2 
x
1
x
)
( 2
1 x
x 
)
( 2
1 x
x
k
F 

k
F
F

6. Translational Mass
Translational Mass
ii)
• Translational Mass is an inertia
element.
• A mechanical system without
mass does not exist.
• If a force F is applied to a mass
and it is displaced to x meters
then the relation b/w force and
displacements is given by
Newton’s law.
M
)
(t
F
)
(t
x
x
M
F 



7. Translational Damper
Translational Damper
iii)
• Damper opposes the rate of
change of motion.
• All the materials exhibit the
property of damping to some
extent.
• If damping in the system is not
enough then extra elements (e.g.
Dashpot) are added to increase
damping.

8. Common Uses of Dashpots
Door Stoppers
Vehicle Suspension
Bridge Suspension
Flyover Suspension

9. Translational Damper
x
C
F 

• Where C is damping coefficient (N/ms-1).
)
( 2
1 x
x
C
F 
 


10. Example-1
• Consider the following system (friction is negligible)
10
• Free Body Diagram
M
F
k
f
M
f
k
F
x
M
• Where and are force applied by the spring and
inertial force respectively.
k
f M
f

11. Example-1
11
• Then the differential equation of the system is:
x
M
kx
F 



• Taking the Laplace Transform of both sides and ignoring
initial conditions we get
M
F
k
f
M
f
M
k f
f
F 

)
(
)
(
)
( s
kX
s
X
Ms
s
F 
 2

12. 12
)
(
)
(
)
( s
kX
s
X
Ms
s
F 
 2
• The transfer function of the system is
k
Ms
s
F
s
X

 2
1
)
(
)
(
• if
1
2000
1000



Nm
k
kg
M
2
001
0
2


s
s
F
s
X .
)
(
)
(
Example-1

13. 13
• The pole-zero map of the system is
2
001
0
2


s
s
F
s
X .
)
(
)
(
Example-2
-1 -0.5 0 0.5 1
0
𝑗 2
Pole-Zero Map
Real Axis
Imaginary
Axis
−𝑗 2

14. Example-2
• Consider the following system
14
• Free Body Diagram
k
F
x
M
C
M
F
k
f
M
f
C
f
C
M
k f
f
f
F 



15. Example-3
15
Differential equation of the system is:
kx
x
C
x
M
F 

 


Taking the Laplace Transform of both sides and ignoring
Initial conditions we get
)
(
)
(
)
(
)
( s
kX
s
CsX
s
X
Ms
s
F 

 2
k
Cs
Ms
s
F
s
X


 2
1
)
(
)
(

16. Example-4
• Consider the following system
16
• Mechanical Network
k
F
2
x
M
1
x B
↑ M
k
B
F
1
x 2
x

17. Example-4
17
• Mechanical Network
↑ M
k
B
F
1
x 2
x
)
( 2
1 x
x
k
F 

At node 1
x
At node 2
x
2
2
1
2
0 x
B
x
M
x
x
k 

 


 )
(

18. Example-6
18
k
)
(t
f
2
x
1
M
4
B
3
B
2
M
1
x
1
B 2
B
↑ M1
k 1
B
)
(t
f
1
x 2
x
3
B
2
B M2
4
B

19. Example-7
• Find the transfer function of the mechanical translational
system given in Figure-1.
19
Free Body Diagram
Figure-1
M
)
(t
f
k
f
M
f
B
f
B
M
k f
f
f
t
f 


)
(
k
Bs
Ms
s
F
s
X


 2
1
)
(
)
(

20. Example-10
20
1
k
)
(t
u
3
x
1
M
4
B
3
B
2
M
2
x
2
B 5
B
2
k 3
k
1
x
1
B

21. Basic Elements of Rotational Mechanical Systems
Rotational Spring
)
( 2
1 
 
 k
T
2

1


22. Basic Elements of Rotational Mechanical Systems
Rotational Damper
2

1

)
( 2
1 
 
 
 C
T
T
C

23. Basic Elements of Rotational Mechanical Systems
Moment of Inertia


J
T 

T
J

24. Example-11
1

T 1
J
1
k
1
B
2
k
2
J
2

3

↑ J1
1
k
T
1
 3

1
B
J2
2

2
k

25. Example-12
↑ J1
1
k
1
B
T
1
 3

2
B
3
B J2
4
B
2

1

T 1
J
1
k
3
B
2
B
4
B
1
B
2
J
2

3


26. Example-13
1

T
1
J
1
k
2
B 2
J
2

2
k