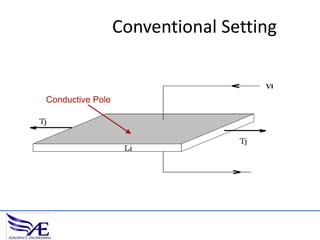
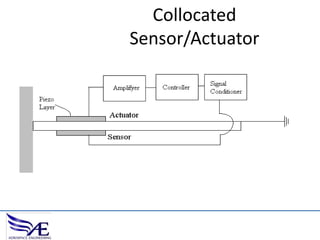
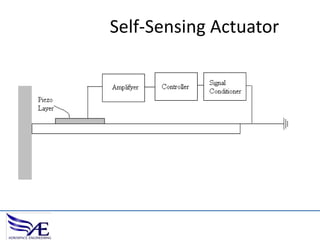
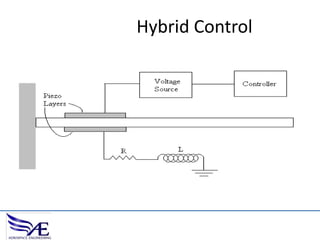
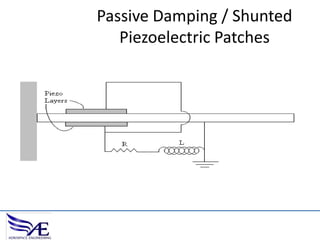
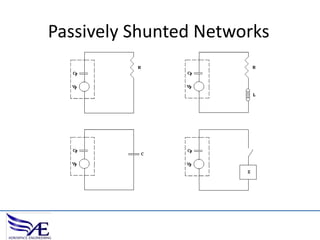
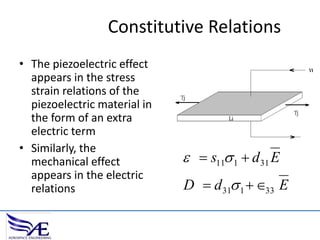
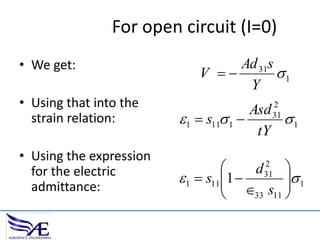
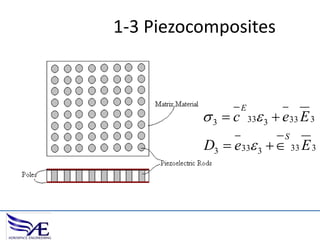
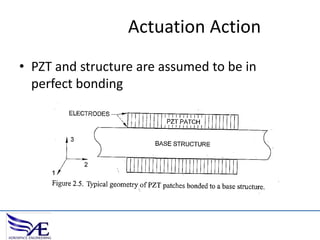
The document discusses piezoelectric materials, which convert mechanical energy to electrical energy and vice versa, detailing their functioning as sensors and actuators. It also covers equations related to the electromechanical coupling and different conditions affecting piezoelectric properties, alongside applications like vibration control and hybrid control systems. Additionally, it provides insights into homework assignments involving piezoelectric beams and the review of thin-beam theory.

1. Piezoelectric Materials
Dr. Mohammad Tawfik

2. What is Piezoelectric
Material?
• Piezoelectric Material is one that possesses
the property of converting mechanical energy
into electrical energy and vice versa.

3. Piezoelectric Materials
• Mechanical Stresses  Electrical Potential
Field : Sensor (Direct Effect)
• Electric Field  Mechanical Strain :
Actuator (Converse Effect)
Clark, Sounders, Gibbs, 1998

4. Conventional Setting
Conductive Pole

5. Piezoelectric Sensor
• When mechanical stresses are applied on the
surface, electric charges are generated
(sensor, direct effect).
• If those charges are collected on a conductor
that is connected to a circuit, current is
generated

6. Piezoelectric Actuator
• When electric potential (voltage) is applied to
the surface of the piezoelectric material,
mechanical strain is generated (actuator).
• If the piezoelectric material is bonded to a
surface of a structure, it forces the structure
to move with it.

7. Applications of Piezoelectric Materials in
Vibration Control

8. Collocated
Sensor/Actuator

9. Self-Sensing Actuator

10. Hybrid Control

11. Passive Damping / Shunted
Piezoelectric Patches

12. Passively Shunted Networks
Resistive
Capacitive
Resonant
Switched

13. Modeling of Piezoelectric
Structures

14. Constitutive Relations
• The piezoelectric effect
appears in the stress
strain relations of the
piezoelectric material in
the form of an extra
electric term
• Similarly, the
mechanical effect
appears in the electric
relations
  s11 1  d 31 E
D  d 31 1  33 E

15. Constitutive Relations
•
•
•
•
‘S’ (capital s) is the strain
‘T’ is the stress (N/m2)
‘E’ is the electric field (Volt/m)
‘s’ (small s) is the compliance; 1/stiffness
(m2/N)
• ‘D’ is the electric displacement, charge per
unit area (Coulomb/m2)

16. The Electromechanical
Coupling
•
Electric permittivity (Farade/m) or
(Coulomb/mV)
• d31 is called the electromechanical coupling
factor (m/Volt)

17. Manipulating the
Equations
• The electric displacement is
the charge per unit area:
• The rate of change of the
charge is the current:
• The electric field is the
electric potential per unit
length:
Q
D
A
1
I
D   Idt 
A
As
V
E
t

18. Using those relations:
• Using the
relations:
• Introducing the
capacitance:
• Or the electrical
admittance:
d 31
 1  s11 1  V
t
A 33 s
I  Ad 31s 1 
V
t
I  Ad 31s 1  CsV
I  Ad 31s 1  YV

19. For open circuit (I=0)
• We get:
• Using that into the
strain relation:
• Using the expression
for the electric
admittance:
Ad 31s
V 
1
Y
2
31
Asd
1  s11 1 
1
tY
2

d 31 
 1
 1  s11 1 
  s 
33 11 


20. The electromechanical
coupling factor
• Introducing the factor ‘k’:
1  s11 1  k  1
2
31
• ‘k’ is called the electromechanical coupling factor
(coefficient)
• ‘k’ presents the ratio between the mechanical energy
and the electrical energy stored in the piezoelectric
material.
• For the k13, the best conditions will give a value of
0.4

21. Different Conditions
• With open circuit conditions, the stiffness of
the piezoelectric material appears to be higher
(less compliance)
1  s11 1  k  1  s  1
2
31
D
• While for short circuit conditions, the stiffness
appears to be lower (more compliance)
  s11  s 
E

22. Different Conditions
• Similar results could be obtained for the
electric properties; electric properties are
affected by the mechanical boundary
conditions.

23. Zero-strain conditions
(S=0)
• Using the
relations:
• Introducing the
capacitance:
• Or the electrical
admittance:
d 31
0  s11 1 
V
t
2

As 33
d 31 
1 
V
I 
t  33 s11 


I  Y 1 k V
2
31

24. Other types of Piezo!

25. 1-3 Piezocomposites
3  c
E
  e33 E 3
33 3
S
D3  e33 3  
33
E3

26. Active Fiber Composites (AFC)
c eff 11  c E11 
e
eff
31

v 
C
2
v p e31
 v p S 33
33
 33e31
v C  33  v p S 33
 33 S 33
 eff 33  C
v  33  v p S 33




27. Actuation Action
• PZT and structure are assumed to be in
perfect bonding

28. Axial Motion of Rods
• In this case, we will consider the case when
the PZT and the structure are deforming
axially only

29. Zero Voltage case
• If the structure is subject to axial force only,
we get:
 a  Ea  a
 s  Es s
• And for the equilibrium:
F  Aa a  As s  Aa Ea a  As Es s
F  Aa a  As s   Aa Ea  As Es  x

30. Zero Voltage case
• From that, we may write the force strain
relation to be:
F
F b
x 

Aa Ea  As Es 2ta Ea  t s Es

31. Zero Force case
• In this case, the strain of the of the PZT will be
less than that induced by the electric field
only!   E   E   E   E d V
a
a s
a
p
a s
a
31
t
 s  Es  s
• For equilibrium, F=0:
V
F  Aa a  As s  Aa Ea s  Aa Ea d31  As Es s  0
t
V
Aa Ea d 31
t
s 
 Aa Ea  As Es 

32. Homework #2
• Solve problems 1,2,&3 from textbook
• Due 27/11/2013 (11:59PM)

33. Beams with Piezoelectric
Material

34. Review of Thin-Beam
Theory
• The Euler-Benoulli beam theory assumes that
the strain varies linearly through the thickness
of the beam and inversely proportional to the
radius of curvature.
d 2v
  y 2
dx
d 2v
  E   Ey 2
dx

35. Equilibrium
• The externally applied moment has to be in
equilibrium with the internally generated
h/2
h/2
moment.
d 2v
M    bydy 
h / 2
 Ey dx
2
h/2
• For homogeneous materials:
2
h/2
d v
d 2v
2
M  E 2  y bdy  EI 2
dx h / 2
dx
bydy

36. Equilibrium
• Rearranging the terms:
M d 2v
 2
EI dx
My
 
I

37. With piezoelectric
materials
• Introducing change in the material property:
h/2
M
   ydy
b
h / 2
t s / 2

V
   Ea   a  d 31  ydy   Es s ydy

ta 


h / 2
t s / 2
ts / 2

V
  Ea   a  d 31  ydy

ta 


ts / 2
h/2

38. With piezoelectric
materials
• Expanding the integral
2
M
d v
 Ea 2
b
dx
ts / 2
V
/ 2y dy  Ea d31 ta
h
ts / 2
 ydy
2
2
ts / 2
h / 2
2
h/2
d v
d v
V
2
2
 Es 2  y dy  Ea 2  y dy  Ea d 31
dx t s / 2
dx t s / 2
ta
h/2
 ydy
ts / 2

39. With piezoelectric
materials
• Rearranging
ts / 2
h/2
 ts / 2 2

M d v
 2 Ea  y dy  Es  y 2 dy  Ea  y 2 dy 

b dx   h / 2
t s / 2
ts / 2


2
V
 Ea d 31
ta
t s / 2
V
/ 2ydy  Ea d31 ta
h
h/2
 ydy
ts / 2

40. With piezoelectric
materials
• Integrating
 





M
1 d 2v
3
3
3

Ea h 3  t s  2 E s t s  Ea h 3  t s
b 24 dx 2
V 2
V 2
2
2
 Ea d 31
t s  h  Ea d 31
h  ts
8t a
8t a

 




Ea d 31V 2
M
1 d 2v
3
3
2
3

Ea h  t s  E s t s 
h  ts
2
b 12 dx
4ta


41. Remember:
• For homogeneous structures: Eh3 d 2v
M

2
12 dx
b
• Thus, in the absence of the voltage:


Ea h  t s  Es t s
EI Equivalent  b
12
• OR:
M  EI Equivalent
3
3
3

d 2 v Ea bd31V 2
2

h  ts
2
dx
4t a


42. In the absence of load
2

Ea bd31V
d v
2
2

h  ts
2
dx
4ta EI Equivalent

• Thus, the structure will feel a moment:

Es I s Eabd31V 2
d 2v
2
M s  Es I s 2  
h  ts
dx
4ta EI Equivalent


43. Piezoelectric forces
• The above is equivalent of having a force
applied by the piezoelectric material that is
equal to:
Ms
Es I s Ea bd 31V 2
2
Fa 
ts

4t s t a EI Equivalent
h
 ts


44. Homework #3
• Solve problems 4,5,&6 from textbook
• Due 30/11/2013 (11:59PM)