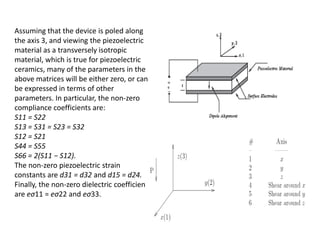
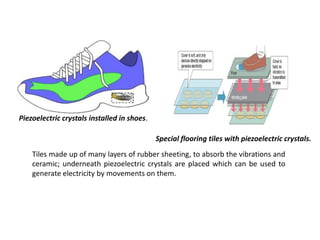
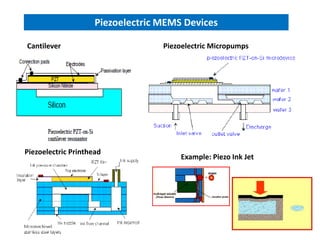
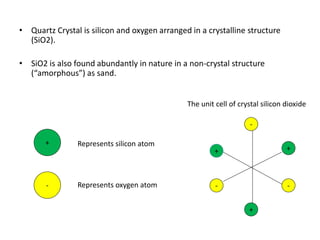
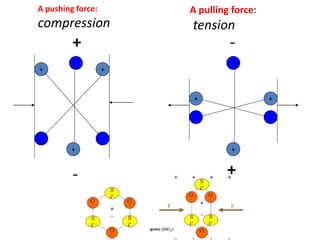
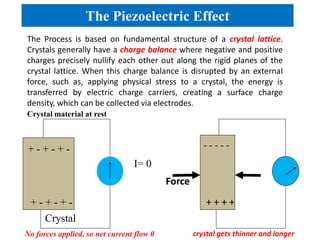
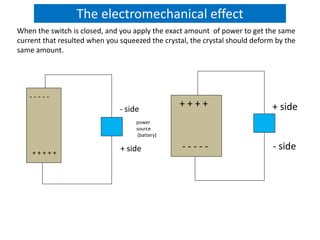
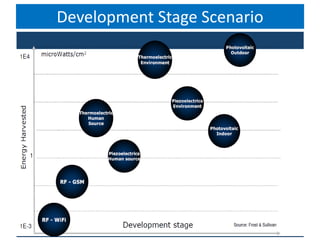
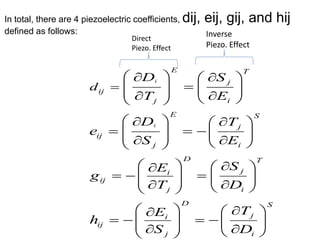Piezoelectricity involves using crystals that generate an electric charge in response to applied mechanical stress. Some materials that exhibit piezoelectricity include quartz, bone, wood, and synthetic ceramics. The document discusses the piezoelectric effect and electromechanical effect at the crystal structure level. It also provides the mathematical descriptions and constitutive equations for relating mechanical and electrical behavior in piezoelectric materials. The main applications discussed are piezoelectric actuators and transducers used in microelectromechanical systems.

1. Piezo-Electricity
zaahir salam
A Solution To Our Growing Energy Crisis

2. Piezoelectricity
• Pierre Curie and Paul
Jacques in 1880

3. Some Real Time Examples

4. Piezoelectric crystals installed in shoes.
Special flooring tiles with piezoelectric crystals.
Tiles made up of many layers of rubber sheeting, to absorb the vibrations and
ceramic; underneath piezoelectric crystals are placed which can be used to
generate electricity by movements on them.

5. Piezoelectric MEMS Devices
Cantilever
Example: Piezo Ink Jet
Piezoelectric Printhead
Piezoelectric Micropumps

6. What is a crystal?
A class of materials arranged in a definite, geometric pattern in
three dimensions (table salt and sugar are common examples)

7. Of the 32 crystal classes, 21are non-centrosymmetric (not having a centre
of symmetry), and of these, 20 exhibit direct piezoelectricity (the 21st is the
cubic class 432).
10 of these represent the polar crystal classes, which show a spontaneous
polarization without mechanical stress due to a non-vanishing electric
dipole moment associated with their unit cell, and which exhibit
pyroelectricity.
If the dipole moment can be reversed by the application of an electric field,
the material is said to be ferroelectric.
Crystal classes
For polar crystals, for which P ≠ 0 holds without applying a mechanical
load, the piezoelectric effect manifests itself by changing the magnitude or
the direction of P or both.
For the non-polar, but piezoelectric crystals, on the other hand, a
polarization P different from zero is only elicited by applying a mechanical
load. For them the stress can be imagined to transform the material from a
non-polar crystal class (P =0) to a polar one, having P ≠ 0.

8. • Quartz Crystal is silicon and oxygen arranged in a crystalline structure
(SiO2).
• SiO2 is also found abundantly in nature in a non-crystal structure
(“amorphous”) as sand.
+ Represents silicon atom
- Represents oxygen atom
The unit cell of crystal silicon dioxide
-
+
+
-
+
-

9. -
+
+
-
+
-
-
+
+
-
+
-
+
-
A pushing force:
compression
A pulling force:
tension
+
-

10. The Piezoelectric Effect
Crystal
I= 0
+ - + - + -
+ - + - + -
The Process is based on fundamental structure of a crystal lattice.
Crystals generally have a charge balance where negative and positive
charges precisely nullify each other out along the rigid planes of the
crystal lattice. When this charge balance is disrupted by an external
force, such as, applying physical stress to a crystal, the energy is
transferred by electric charge carriers, creating a surface charge
density, which can be collected via electrodes.
Crystal material at rest
No forces applied, so net current flow 0
- - - - -
+ + + +
Force
crystal gets thinner and longer

11. The electromechanical effect
When the switch is closed, and you apply the exact amount of power to get the same
current that resulted when you squeezed the crystal, the crystal should deform by the
same amount.
power
source
(battery)
- side
+ side
- - - - -
+ + + + +
+ side
- side
+ + + +
- - - - -

12. Summary of the Piezoelectric & Electromechanical Effect
• A deformation of the crystal structure (eg: squeezing it) will
result in an electrical current.
• Changing the direction of deformation (eg: pulling it) will
reverse the direction of the current.
• If the crystal structure is placed into an electrical field, it will
deform by an amount proportional to the strength of the field.
• If the same structure is placed into an electrical field with the
direction of the field reversed, the deformation will be
opposite.

13. Materials
• Many materials, both natural and synthetic, exhibit piezoelectricity:
• Naturally occurring crystals
 Berlinite (AlPO4), a rare phosphate mineral that is structurally identical
to quartz
 Sucrose (table sugar)
 Quartz
 Rochelle salt
 Topaz
 Tourmaline-group minerals
• Bone
Fukada et al. Not due to the apatite crystals, which are
centrosymmetric, thus non-piezoelectric, but due to collagen.
Collagen exhibits the polar uniaxial orientation of molecular
dipoles in its structure and can be considered as bioelectret, a sort
of dielectric material exhibiting quasipermanent space charge and
dipolar charge.

14. Other natural materials
Biological materials exhibiting piezoelectric properties include:
Tendon
Silk
Wood due to piezoelectric texture
Enamel
Dentin
DNA
Synthetic crystals
Gallium orthophosphate (GaPO4), a quartz analogic crystal
Langasite (La3Ga5SiO14), a quartz analogic crystal
Synthetic
ceramics
Barium titanate (BaTiO3)
Lead titanate (PbTiO3)
Lead zirconate titanate (Pb[ZrxTi1−x]O3 0≤x≤1)
Polymers
Polyvinylidene fluoride (PVDF)

15. Which Materials should be used for
energy harvesting?

16. Development Stage Scenario

17. Market Impact of Top 10 Developed
Piezoelectrics

18. DOES PURE SILICON ACT AS APIEZOELECTRIC MATERIAL OR NOT
• Although silicon is a simple cubic crystal, it can be induced to
have a piezoelectric response, by making pores in it and thus
spoiling its symmetry. By etching a silicon wafer into porous
material, we found that it responds to voltage applied to it, as
well as to light.
Piezoelectric and piezooptic effects in porous silicon
Shirly Vinikman-Pinhasi and Erez N. Ribak

19. Only pure quartz crystal or rock crystal, untwinned,
clear, free from any inclusion, has an important
property:
It expands (mechanically) under the influence of
electric current and conversely pressure induces a
measurable electric current. This property is known
as piezoelectricity. The current thus developed is
called piezoelectric current.
DOES SILICA AS GENERAL SHOW PIEZOELECTRICITY OR NOT?

20. Piezoelectric Constitutive Equations
 The equations which describe electromechanical properties of
piezoelectric materials.
 The IEEE standard assumes that piezoelectric materials are linear.
 It turns out that at low electric fields and at low mechanical stress
levels piezoelectric materials have a linear profile. However, they
may show considerable nonlinearity if operated under a high
electric field or high mechanical stress level.
 Total strain in the transducer is the sum of mechanical strain
induced by the mechanical stress and the controllable actuation
strain caused by the applied electric voltage.

21. Mathematical description
• Piezoelectricity is the combined
effect of the electrical behaviour of
the material:
• Where D is electric charge
displacement , is pemittivity
and E is electric field strength.
• Hooke’s Law:
S=sT
Where S is Strain, s is compliance and T is
stress
D E

Schematic diagram of a piezoelectric transducer
Elastic compliance, s, is the strain produced in a piezoelectric material per unit of stress
applied and, for the 11 and 33 directions, is the reciprocal of the modulus of elasticity
(Young's modulus, Y). sD is the compliance under a constant electric displacement; sE is
the compliance under a constant electric field.

22. • These may be combined into so called coupled equations, of which the
strain-charge form is:
Where [d] is the matrix for the direct piezoelectric effect and [dt] is the matrix for the
converse piezoelectric effect. The superscript E indicates a zero, or constant, electric field; the
superscript T indicates a zero, or constant, stress field; and the superscript t stands for
transposition of a matrix.
      
     t T
E
S s T d E
D d T E
  
 
        
where the indexes i, j = 1, 2, . . . ,6
and m, k = 1, 2, 3 refer to different
directions within the material
coordinate system.

23. where
σ . . . stress vector (N/m2)
ε . . . strain vector (m/m)
E. . . vector of applied electric field (V/m)
ξ . . . permittivity (F/m)
d . . . matrix of piezoelectric strain constants(m/V )
S . . . matrix of compliance coefficients (m2/N)
D. . . vector of electric displacement (C/m2)
g . . . matrix of piezoelectric constants (m2/C)
β . . . impermitivity component (m/F)
the superscripts D, E, and σ represent measurements taken
at constant electric displacement, constant electric field and constant
stress.

24. Assuming that the device is poled along
the axis 3, and viewing the piezoelectric
material as a transversely isotropic
material, which is true for piezoelectric
ceramics, many of the parameters in the
above matrices will be either zero, or can
be expressed in terms of other
parameters. In particular, the non-zero
compliance coefficients are:
S11 = S22
S13 = S31 = S23 = S32
S12 = S21
S44 = S55
S66 = 2(S11 − S12).
The non-zero piezoelectric strain
constants are d31 = d32 and d15 = d24.
Finally, the non-zero dielectric coefficients
are eσ11 = eσ22 and eσ33.

25. 1 1 3111 12 13
2 2 3221 22 23
3 3 3331 32 33
44 2444
5 155 55
666 11 126
0 00 0 0
0 00 0 0
0 00 0 0
0 00 0 0 0 0
0 00 0 0 0 0
0 0 00 0 0 0 0 2( )
E E E
E E E
E E E
E
E
E E E
S T ds s s
S T ds s s
S T ds s s
TS ds
T dS s
Ts s sS
 
 
     
     
    
    
    
    
    
           
1
2
3
E
E
E


  
  
  
    
 

The strain for a material of the 4mm (C4v) crystal class (such as a poled piezoelectric ceramic
such as tetragonal PZT or BaTiO3) as well as the 6mm crystal class may also be written as
(ANSI IEEE 176):
Relationship for the direct piezoelectric effect

26. 1
2
1 15 11 1
3
2 24 22 2
4
31 32 33 33 33
5
6
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0
T
T
D d E
T
D d E
T
d d d ED
T
T

  

 
 
        
        
        
                
 
 
Relationship for the converse piezoelectric effect
Generally D and E are vectors , that is, Cartesian tensor of rank-1;
permittivity ε is Cartesian tensor of rank 2.
Strain and stress are, in principle, also rank-2 tensors.
But conventionally, because strain and stress are all symmetric tensors, the subscript of strain
and stress can be re-labeled in the following fashion: 11 → 1; 22 → 2; 33 → 3; 23 → 4; 13 → 5;
12 → 6. (Different convention may be used by different authors in literature. Say, some use 12 →
4; 23 → 5; 31 → 6 instead.) That is why S and T appear to have the "vector form" of 6
components. Consequently, s appears to be a 6 by 6 matrix instead of rank-4 tensor.
Such a re-labeled notation is often called Voigt notation.
Charge Relationship

27. In total, there are 4 piezoelectric coefficients, dij, eij, gij, and hij
defined as follows:
i
i
E T
j
ij
j i
E S
j
ij
j i
D T
ji
ij
j i
D S
ji
ij
j i
d
D S
T E
D T
e
S E
SE
g
T D
TE
h
S D

   
       
   
         
   
         
   
          
Direct
Piezo. Effect
Inverse
Piezo. Effect

28. • The principal applications of the piezoelectric effect in MEMS and
microsystems, however are in actuators, dynamic signal transducers for
pressure sensors and accelerometers.
• The effectiveness of the conversion of mechanical to electrical energies
and vice versa can be assessed by the electromechanical conversion
factor K defined as follows (Kasap 1997)
WITH RESPECT TO MEMS/MICROSYSTEMS THE
CONSTITUTIVE EQUATIONS CAN BE SIMPLIFIED
2 . . .
. . .
output of mechanical energy
K
input of electrical energy

2 . . .
. . .
output of electrical energy
K
input of mechanical energy

OR

29. • The following simple mathematical relationships between the
electromechanical effects can be used in the design of piezoelectric
transducers in a unidirectional loading situation (Askeland, 1994).
• 1) The electric field produced by stress:
where V is the generated electric field in volts per meter and σ, in pascals
is the stress in the piezoelectric crystal induced by applied mechanical
load. The coefficient f is constant.
2)The mechanical strain produced due to electric field:
where ϵ is the induced strain and V is the applied electric field in volts per
meter. The piezoelectric coefficient d.
The coefficients f and d in the above equations have the relationship
V f 
Vd
1
E
fd

Here E is the Young’s Modulus of the piezoelectric crystals.

30. Squeezed virus produces electricity
A bioengineered thin film of M13 bacteriophage shows piezoelectric properties
that are promising for small-scale device integration. S. Michael Yu
The surface of an M13 bacteriophage is
covered with densely packed identical α-helical
coat proteins aligned at a 20° angle with
respect to the axis of the virus (dashed line).
These proteins have an intrinsic electric dipole
moment because they have a positive (blue)
and a negative end (red), and this leads to
piezoelectric effects in thin films of M13
bacteriophage.
b) It is because of compressing the M13 virus
from above (blue arrow) causes neighbouring
protein helices on the virus surface to rub
against each other (purple arrows) resulting in
deformation (green arrows) of the helical
structure and development of new electric
dipole moments.

31. • Despite rapid advances in the design and fabrication of
miniaturized sensors and devices, their practical applications
have been impeded by the lack of suitably miniscule sources
of electrical power.
• Micro and nanoscale devices — such as ultrasensitive
chemical and biomolecular sensors, nanorobotics,
microelectromechanical systems (MEMS), environmental
sensors and other personal electronic devices — have energy
requirements that are not fully met by available
technologies such as batteries.
• Goal is to develop scalable power generators that can
scavenge energy from ambient sources such as mechanical
vibrations, acoustic energy, thermal gradients and
electromagnetic waves (including light).

32. Flexible approach pays off
• Researchers have managed to extract electrical energy from environmental
noise by exploiting the piezoelectric properties of zinc oxide nanowires with a
device that could herald a new generation of local power sources.
As low-frequency ambient vibrations
move the brushes back and forth relative
to each other, the resulting bending of
the nanowires is converted into electrical
energy.
The approach offers a novel, adaptable,
mobile and cost-effective technical
platform for harvesting energy from the
environment, and could have applications
in powering a wide range of nanodevices
and nanosystems, especially networks of
sensors that are distributed over a large
(and sometimes remote or hostile)
geographic area.
Thomas Thundat Oak Ridge National
Laboratory, USA.

33. KARIN M. RABE
In a recent issue of Nature, Grinberg et al.2 present a theoretical breakthrough
in the analysis of the crystal structure of PZT (PbZr1–xTixO3), the best-studied
mixed-perovskite compound, and the most technologically important, being
widely used both in transducer and capacitor applications.

34. IBM SYSTEMS JOURNAL, VOL 35, NOS 3&4,
1996
Batteries add size, weight, and inconvenience to present-day
mobile computers. This paper explores the possibility of
harnessing the energy expended during the user's everyday
actions to generate power for his or her computer, thus
eliminating the impediment of batteries. An analysis of power
generation through leg motion is presented in depth, and a
survey of other methods such as generation by breath or blood
pressure, body heat, and finger and limb motion is also
presented.

36. The interest in application of all kinds of electronic devices and everyday’s demand on
implementation of microelectromechanical systems in the last decade has produced rapid
progress in the efforts of miniaturizing sensors and actuators. This paper describes microsystem
with integrated power source on piezoelectric principle with pressure sensor. It's meant to be
implemented without any physical contact to the outside world. It is energy sufficient and easy
to produce with printing technology. It uses the PVDF polymer material.

38. THANK YOU