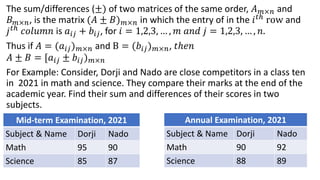
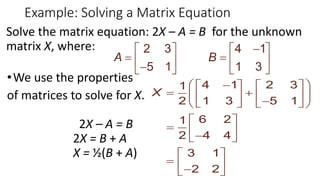1. Addition and subtraction are basic matrix operations where corresponding elements are added or subtracted if the matrices have the same order. 2. Matrix multiplication is also a basic operation on matrices. 3. For matrix addition and subtraction to be defined, the matrices must have the same number of rows and columns. For matrix multiplication to be defined, the number of columns of the first matrix must be equal to the number of rows of the second matrix.

1. Operation on Matrices
Addition, subtraction and multiplication are the basic
operations on the matrix.
Addition & subtraction:Two matrices must have same order
and add or subtract their corresponding or matching elements.
Example: If 𝑨 =
𝟒 𝟑
𝟑 𝟐
𝟐 𝟎
𝒂𝒏𝒅 𝑩 =
𝟐 𝟏
𝟏 𝟎
𝟑 𝟏
, Then
𝐴 + 𝐵 =
𝟒 𝟑
𝟑 𝟐
𝟐 𝟎
+
𝟐 𝟏
𝟏 𝟎
𝟑 𝟏
=
𝟒 + 𝟐 𝟑 + 𝟏
𝟑 + 𝟏 𝟐 + 𝟎
𝟐 + 𝟑 𝟎 + 𝟏
=
𝟔 𝟒
𝟒 𝟐
𝟓 𝟏
𝐴 − 𝐵 =
𝟒 𝟑
𝟑 𝟐
𝟐 𝟎
−
𝟐 𝟏
𝟏 𝟎
𝟑 𝟏
=
𝟒 − 𝟐 𝟑 − 𝟏
𝟑 − 𝟏 𝟐 − 𝟎
𝟐 − 𝟑 𝟎 − 𝟏
=
𝟐 𝟐
𝟐 𝟐
−𝟏 −𝟏

2. The sum/differences (±) of two matrices of the same order, 𝐴𝑚×𝑛 and
𝐵𝑚×𝑛, is the matrix (𝐴 ± 𝐵)𝑚×𝑛 in which the entry of in the 𝑖𝑡ℎ
row and
𝑗𝑡ℎ
𝑐𝑜𝑙𝑢𝑚𝑛 is 𝑎𝑖𝑗 + 𝑏𝑖𝑗, for 𝑖 = 1,2,3, … , 𝑚 𝑎𝑛𝑑 𝑗 = 1,2,3, … , 𝑛.
Thus if 𝐴 = (𝑎𝑖𝑗)𝑚×𝑛 and B = (𝑏𝑖𝑗)𝑚×𝑛, 𝑡ℎ𝑒𝑛
𝐴 ± 𝐵 = [𝑎𝑖𝑗 ± 𝑏𝑖𝑗)𝑚×𝑛
For Example: Consider, Dorji and Nado are close competitors in a class ten
in 2021 in math and science. They compare their marks at the end of the
academic year. Find their sum and differences of their scores in two
subjects.
Mid-term Examination, 2021
Subject & Name Dorji Nado
Math 95 90
Science 85 87
Annual Examination, 2021
Subject & Name Dorji Nado
Math 90 92
Science 88 89

3. Student Activity.
Is it possible to define the matrix 𝐴 + 𝐵, when
i) A has 3 rows and B has 2 rows
ii) A has 3 columns and B has 2 columns
iii) A has 3 rows and B has 2 columns
iv) Both A and B are square matrices of the same order.
Solution:

4. Negative of the Matrix
The negative of the matrix 𝐴𝑚×𝑛 denoted by −𝐴𝑚×𝑛 is the
matrix formed by replacing each entry in the matrix 𝐴𝑚×𝑛
with the additive inverse. For Example,
If 𝐴2×3 =
3 2 −4
−1 −2 5
, then −𝐴2×3 =
−3 −2 4
1 2 −5
𝐷𝑒𝑓𝑛
: 𝐼𝑓 𝐴 = (𝑎𝑖𝑗)𝑚×𝑛 and 𝑋 is any matrix of the same order
such that 𝐴 + 𝑋 = 0, the zero matrix, then 𝑋 is called the
additive inverse of A. That is 𝑋 = −𝐴.
Find the additive inverse of 𝐴 =
−5 3
7 0
1 −2
?

6. Theorem: If 𝐴 ∈ 𝑆𝑚×𝑛 𝑎𝑛𝑑 𝐵 ∈ 𝑆𝑚×𝑛, where 𝑚, 𝑛 are any
given natural numbers and 𝑐 ∈ 𝑅, 𝑑 ∈ 𝑅, 𝑡ℎ𝑒𝑛

7. Let A, B, and C be m x n matrices and let c and d be
scalars.

8. Example: Solving a Matrix Equation
Solve the matrix equation: 2X – A = B for the unknown
matrix X, where: 2 3 4 1
5 1 1 3
A B

   
 
   

   
•We use the properties
of matrices to solve for X.
2X – A = B
2X = B + A
X = ½(B + A)
4 1 2 3
1
2 1 3 5 1
6 2
1
2 4 4
3 1
2 2
X
 

   
 
 
   

   
 
 
  

 
 
  

 