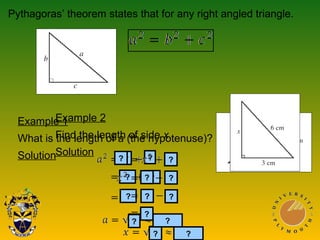
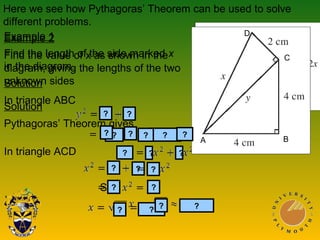
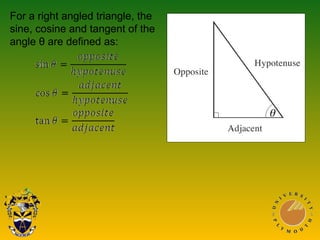
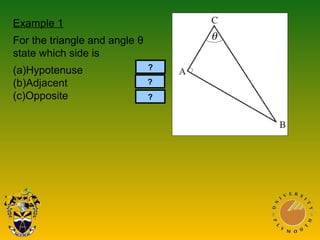
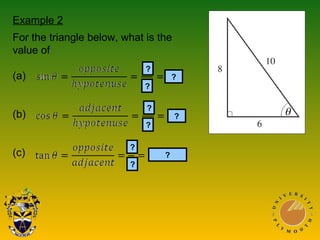
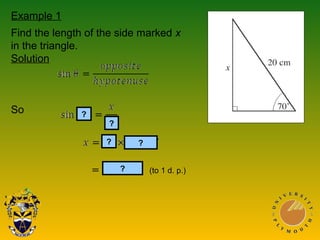
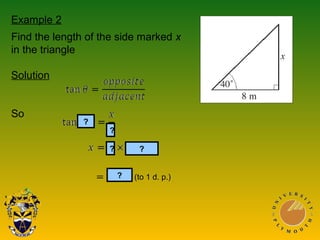
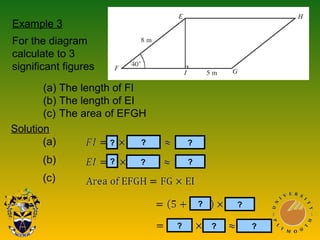
The document covers Pythagoras' theorem and trigonometric ratios, detailing methods to find side lengths in right-angled triangles. It includes various examples for understanding and applying the theorem, as well as definitions for sine, cosine, and tangent ratios. The content is structured across multiple presentations, providing step-by-step solutions to the problems.

1. Unit 34
Pythagoras’ Theorem and
Trigonometric Ratios
Presentation 1 Pythagoras’ Theorem
Presentation 2 Using Pythagoras’ Theorem
Presentation 3 Sine, Cosine and Tangent Ratios
Presentation 4 Finding the Lengths of Sides in Right Angled Triangles

2. Unit 34
34.1 Pythagoras’ Theorem

3. Pythagoras’ theorem states that for any right angled triangle.
Example 1
What is the length of a (the hypotenuse)?
Solution
??
?
??
??
Example 2
Find the length of side x.
Solution
?
?
??
??
?
?
?

4. Unit 34
34.2 Using Pythagoras’ Theorem

5. Example 1
Find the length of the side marked x
in the diagram.
Solution
In triangle ABC
In triangle ACD
Example 2
Find the value of x as shown in the
diagram, giving the lengths of the two
unknown sides
Solution
Pythagoras’ Theorem gives
So
Here we see how Pythagoras’ Theorem can be used to solve
different problems.
?
??
???
??
?
?
?
??
?
??
?
?
?
?
C
BA
D

6. Unit 34
34.3 Sine, Cosine and Tangent

7. For a right angled triangle, the
sine, cosine and tangent of the
angle θ are defined as:

8. Example 1
For the triangle and angle θ
state which side is
(a)Hypotenuse CB
(b)Adjacent AC
(c)Opposite AB
?
?
?

9. Example 2
For the triangle below, what is the
value of
(a)
(b)
(c)
?
?
?
?
?
?
?
?
?

10. Unit 34
34.4 Finding the Lengths of sides
in Right Angled Triangles

11. Example 1
Find the length of the side marked x
in the triangle.
Solution
So
?
?
?
??
(to 1 d. p.)

12. Example 2
Find the length of the side marked x
in the triangle
Solution
So
?
?
?
??
(to 1 d. p.)

13. Example 3
For the diagram
calculate to 3
significant figures
(a) The length of FI
(b) The length of EI
(c) The area of EFGH
Solution
(a)
(b)
(c)
?
?
?
?
?
?
?
?
? ?
?