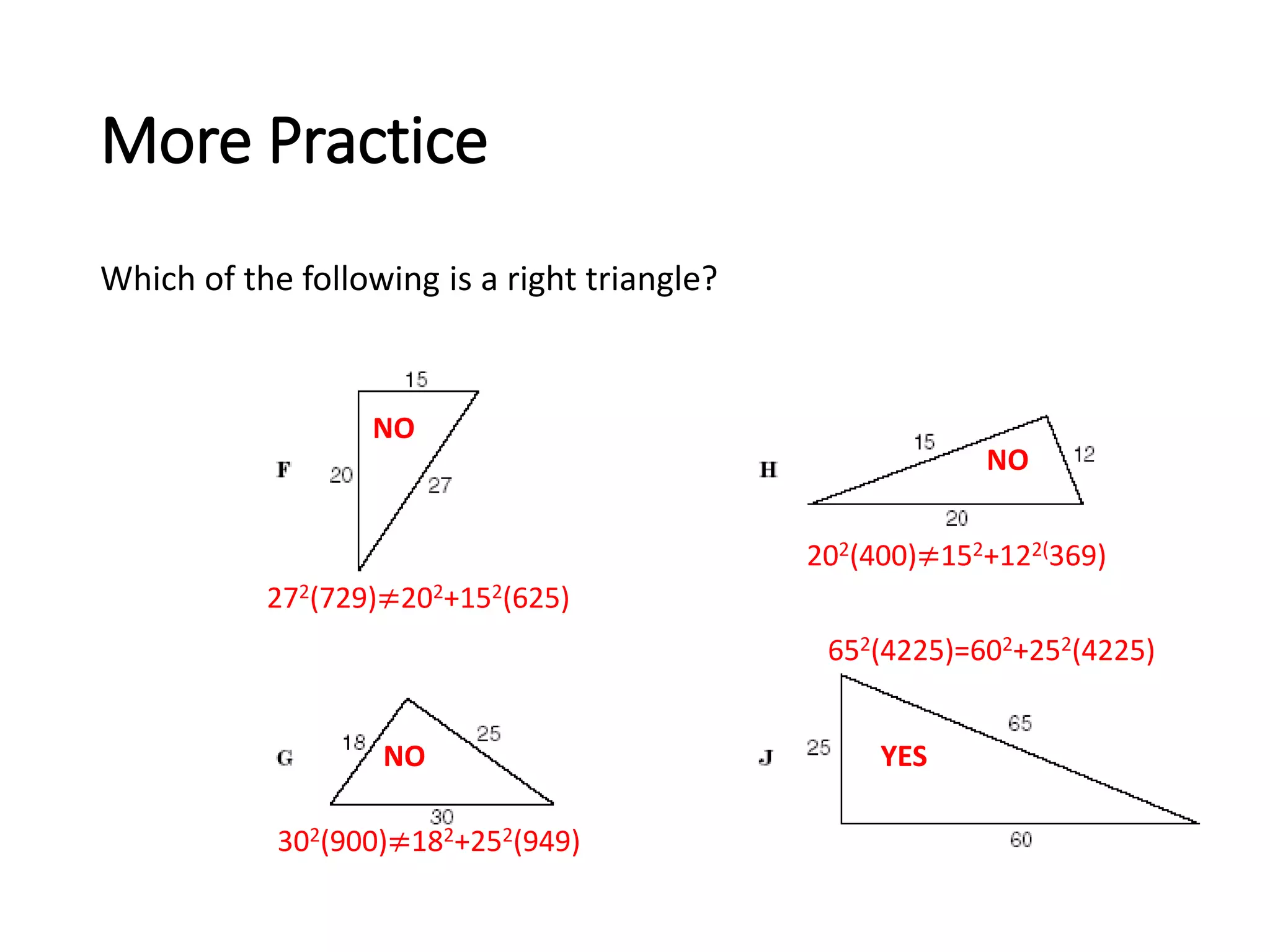
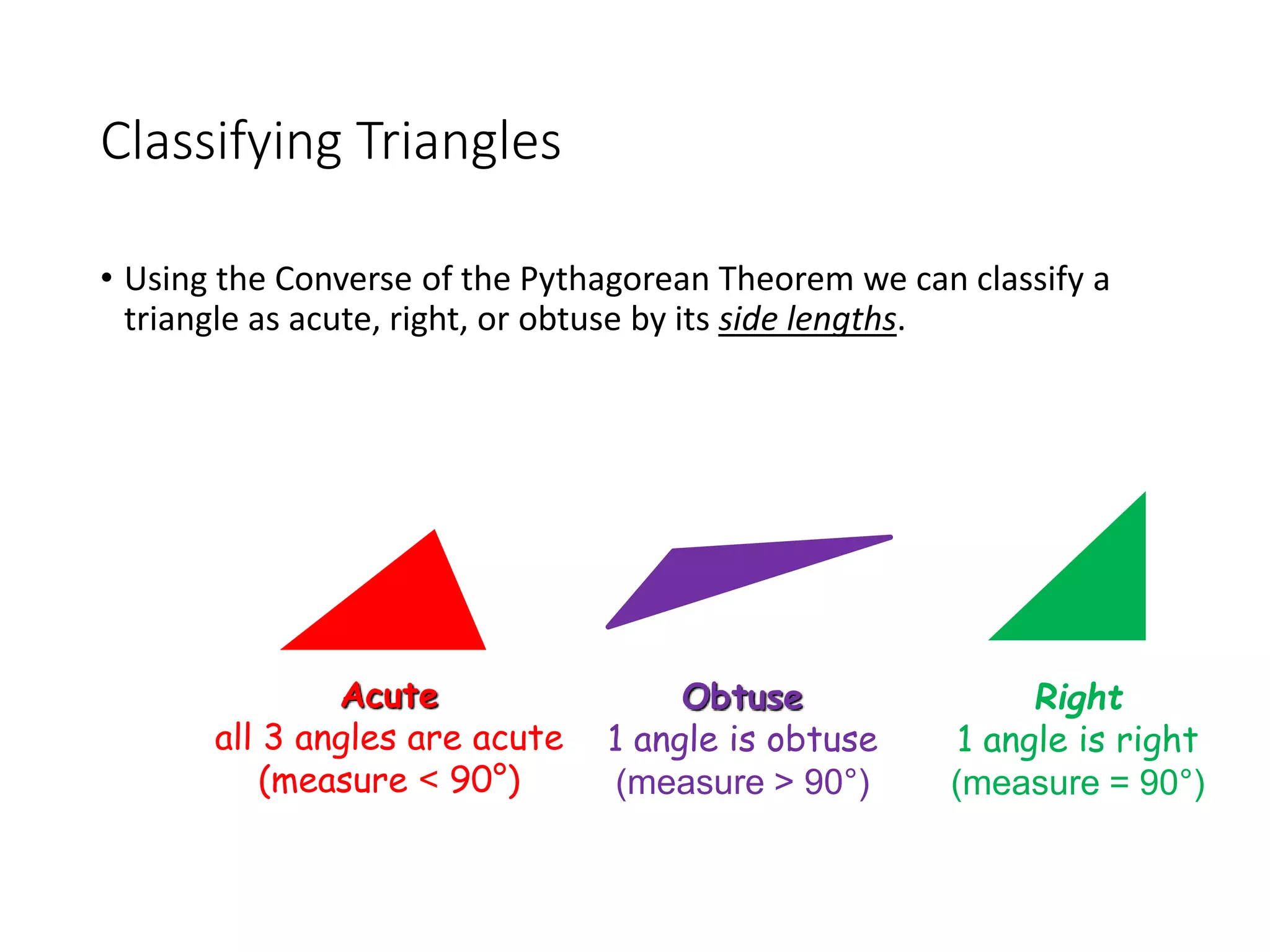
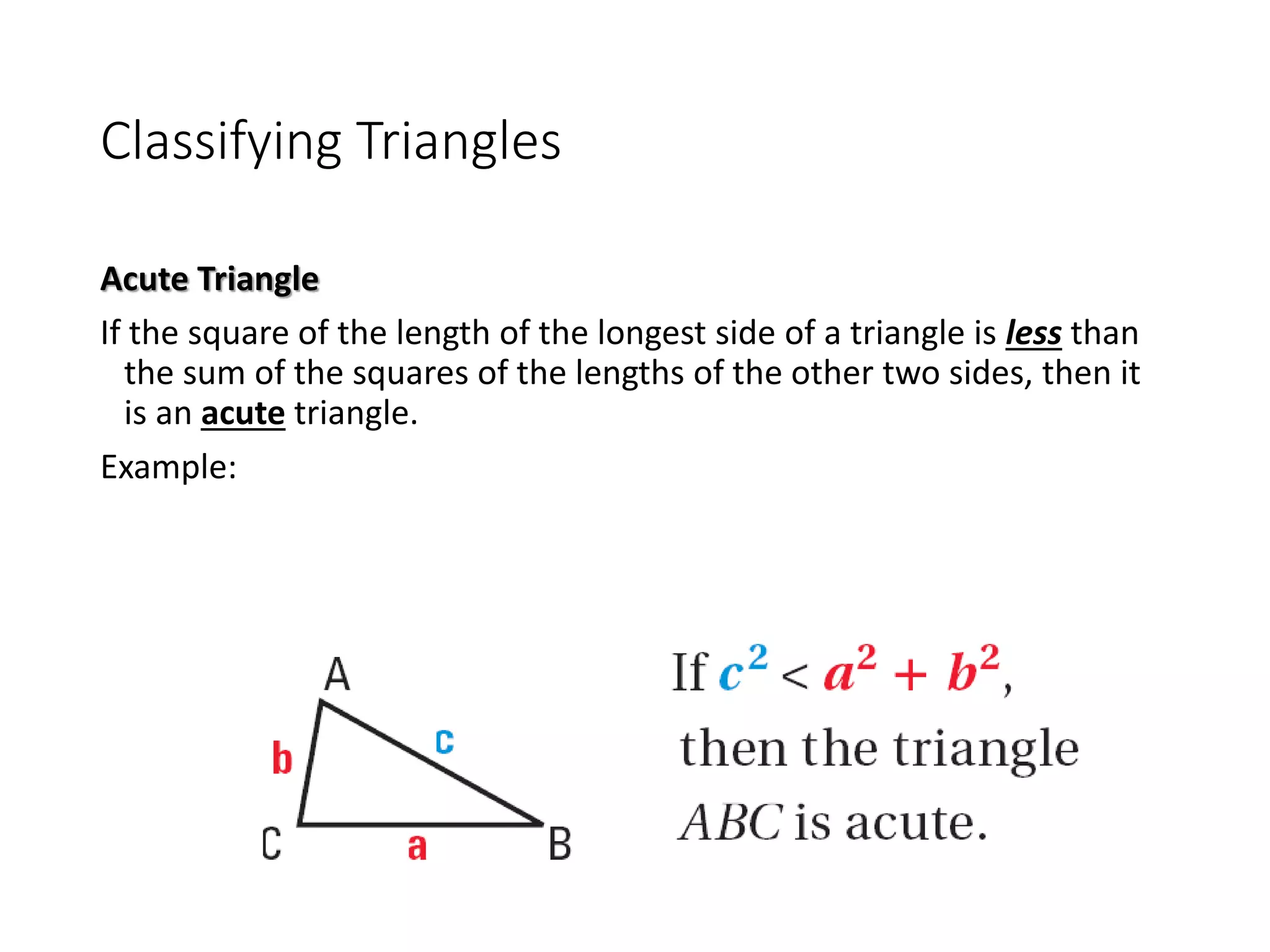
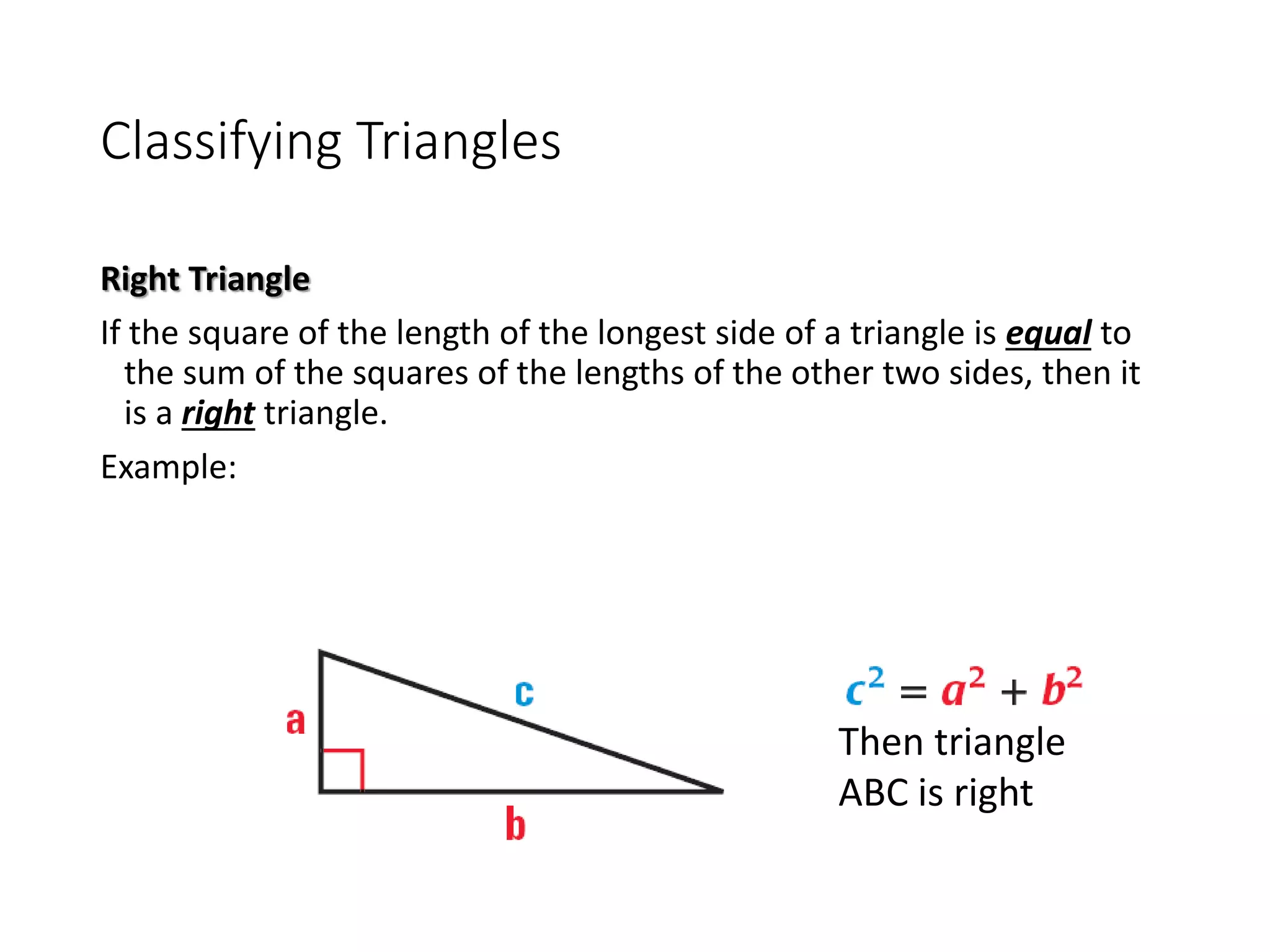
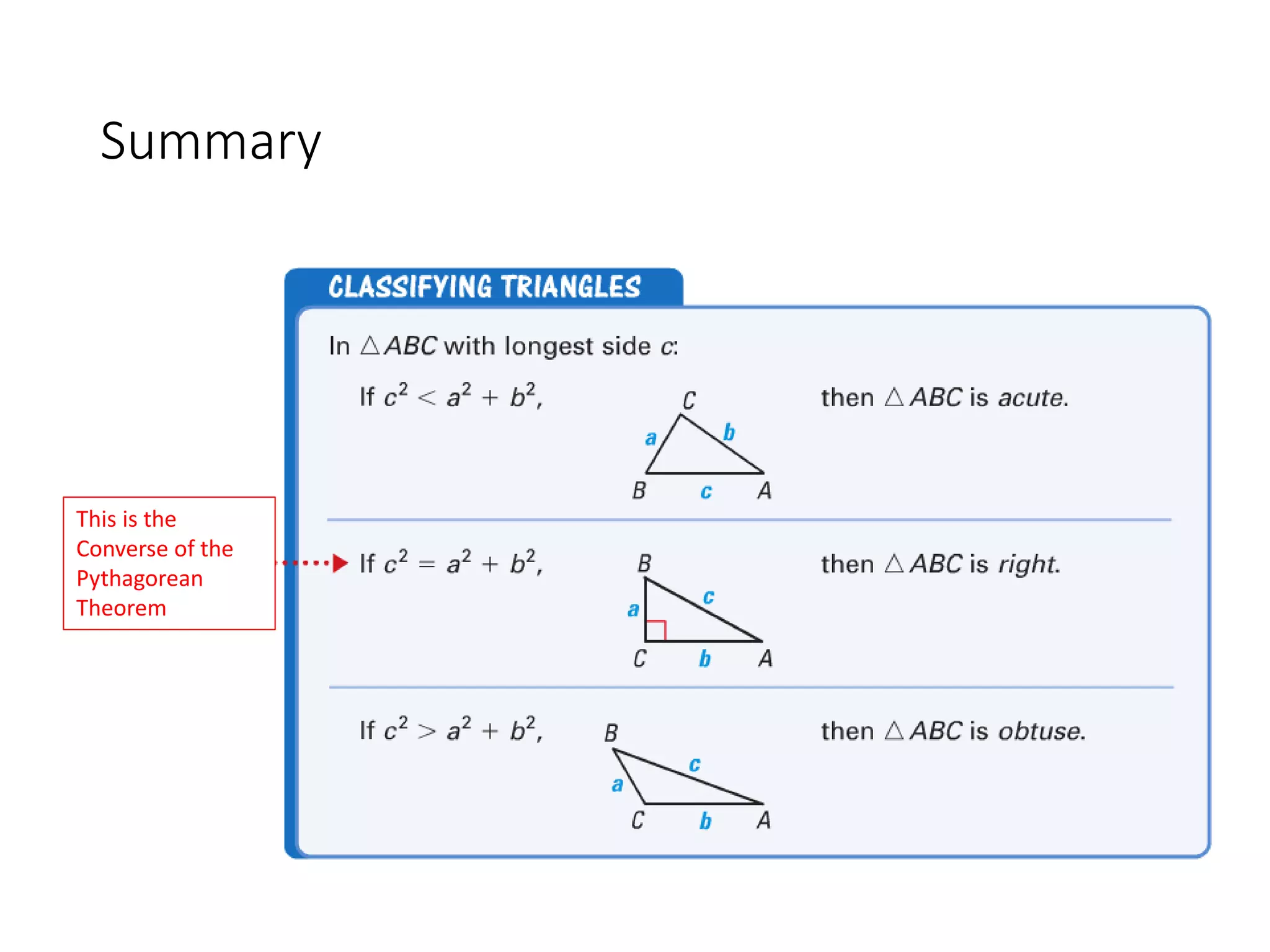
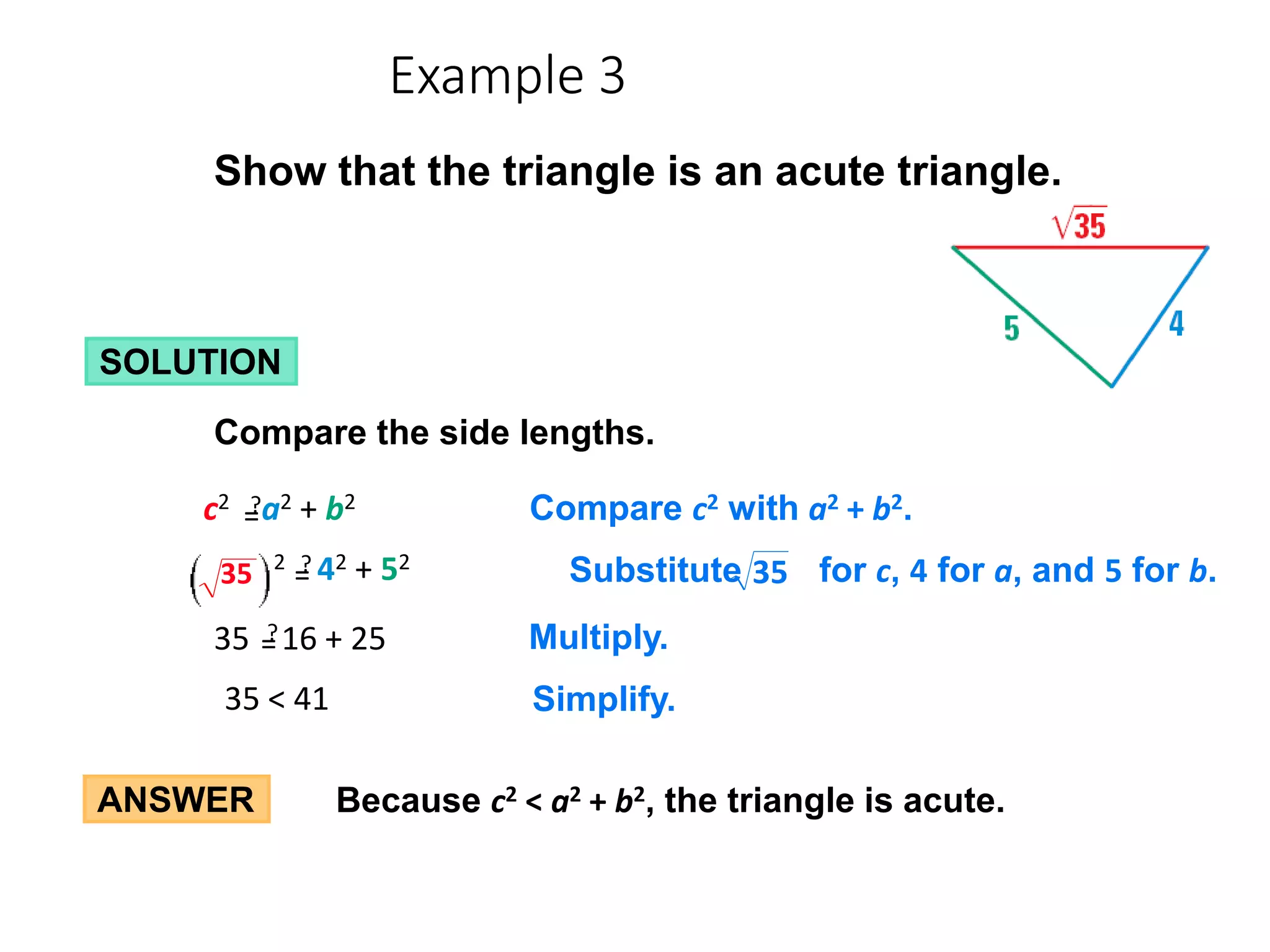
This document discusses the converse of the Pythagorean theorem and how to classify triangles as right, acute, or obtuse based on the lengths of their sides. The converse of the Pythagorean theorem states that if the square of the longest side of a triangle equals the sum of the squares of the other two sides, then the triangle is right. If the square of the longest side is less than the sum of the squares of the other two sides, the triangle is acute. If it is greater, the triangle is obtuse. Several examples are provided to demonstrate how to use side lengths to determine the type of triangle.

1. The Converse Of The
Pythagorean Theorem

2. Objectives:
•Use the Converse of the Pythagorean
Theorem.
•Use side lengths to classify triangles by their
angles.

3. Converse of the Pythagorean Theorem
The converse of the Pythagorean Theorem
If the square of the length of the longest side of a
triangle is equal to the sum of the squares of the
lengths of the other two sides, then it is a right
triangle.
Example:

4. ANSWER It is true that c2 = a2 + b2. So, ∆ABC is a right triangle.
Is ∆ABC a right triangle?
SOLUTION
Let c represent the length of the longest side of the
triangle. Check to see whether the side lengths satisfy the
equation c2 = a2 + b2.
400 = 400 Simplify.
Compare c2 with a2 + b2.
c2 a2 + b2
?
=
=
Multiply.
400 144 + 256
?
=
=
Substitute 20 for c, 12 for a, and 16 for b.
202 122 + 162
?
=
=
Example 1

5. Determine whether 9, 12, and 15 are the sides of a right
triangle.
Since the measure of the longest side is 15, 15 must be c. Let a and
b be 9 and 12.
Pythagorean Theorem
Simplify.
Add.
Example 2a:
Answer: These segments form the sides of a right triangle since
they satisfy the Pythagorean Theorem.

6. Determine whether 21, 42, and 54 are the sides of a
right triangle.
Pythagorean Theorem
Simplify.
Add.
Answer: Since segments with these
measures cannot form a right triangle.
Example 2b:

7. Pythagorean Theorem
Simplify.
Add.
Determine whether 4√3, 4, and 8 are the sides of a right
triangle.
Answer: Since 64 = 64, segments with these measures
form a right triangle.
Example 2c:

8. Answer: The segments form the sides of a right triangle.
Answer: The segments do not form the sides of a right triangle.
Answer: The segments form the sides of a right triangle.
Your Turn:
Determine whether each set of measures are the sides
of a right triangle.
a. 6, 8, 10
b. 5, 8, 9
c.

9. More Practice
Which of the following is a right triangle?
272(729)≠202+152(625)
202(400)≠152+122(369)
302(900)≠182+252(949)
652(4225)=602+252(4225)
NO
NO
NO YES

10. Classifying triangles

11. Classifying Triangles
• Using the Converse of the Pythagorean Theorem we can classify a
triangle as acute, right, or obtuse by its side lengths.
Obtuse
1 angle is obtuse
(measure > 90°)
Right
1 angle is right
(measure = 90°)
Acute
all 3 angles are acute
(measure < 90°)

12. Classifying Triangles
Acute Triangle
If the square of the length of the longest side of a triangle is less than
the sum of the squares of the lengths of the other two sides, then it
is an acute triangle.
Example:

13. Classifying Triangles
Right Triangle
If the square of the length of the longest side of a triangle is equal to
the sum of the squares of the lengths of the other two sides, then it
is a right triangle.
Example:
Then triangle
ABC is right

14. Classifying Triangles
Obtuse Triangle
If the square of the length of the longest side of a triangle is greater
than the sum of the squares of the lengths of the other two sides,
then it is an obtuse triangle.
Example:

15. Summary
This is the
Converse of the
Pythagorean
Theorem

16. ANSWER Because c2 < a2 + b2, the triangle is acute.
Show that the triangle is an acute triangle.
SOLUTION
Compare the side lengths.
35 < 41 Simplify.
Compare c2 with a2 + b2.
c2 a2 + b2
?
=
=
Multiply.
35 16 + 25
?
=
=
Substitute for c, 4 for a, and 5 for b.
35
2 42 + 52
?
=
=
35
Example 3

17. ANSWER Because c2 > a2 + b2, the triangle is obtuse.
Show that the triangle is an obtuse triangle.
SOLUTION
Compare the side lengths.
225 > 208 Simplify.
c2 a2 + b2 Compare c2 with a2 + b2.
?
=
=
(15)2 82 + 122 Substitute 15 for c, 8 for a, and 12 for b.
?
=
=
225 64 + 144 Multiply.
?
=
=
Example 4

18. ANSWER Because c2 > a2 + b2, the triangle is obtuse.
Classify the triangle as acute, right, or obtuse.
SOLUTION
Compare the square of the length of the longest side with
the sum of the squares of the lengths of the two shorter
sides.
64 > 71 Simplify.
64 25 + 36 Multiply.
?
=
=
82 52 + 62 Substitute 8 for c, 5 for a, and 6 for b.
?
=
=
c2 a2 + b2 Compare c2 with a2 + b2.
?
=
=
Example 5

19. Classify the triangle with the given side lengths as
acute, right, or obtuse.
a. 4, 6, 7 b. 12, 35, 37
49 < 52 1369 = 1369
The triangle is acute. The triangle is right.
SOLUTION
a. c2 a2 + b2
?
=
= b. c2 a2 + b2
?
=
=
372 122 + 352
?
=
=
72 42 + 62
?
=
=
1369 144 + 1225
?
=
=
49 16 + 36
?
=
=
Example 6

20. ANSWER obtuse; 62 > 22 + 52
36 >29
ANSWER right; 172 = 82 + 152
289 = 289
ANSWER acute; 72 < 72 + 72
49 < 98
Classify the triangle as acute, right, or obtuse. Explain.
1.
2.
3.
Your Turn:

21. ANSWER acute
ANSWER right
ANSWER obtuse
Use the side lengths to classify the triangle as
acute, right, or obtuse.
4. 7, 24, 24
5. 7, 24, 25
6. 7, 24, 26
Your Turn:

22. Example 7
Classify the triangle with lengths 9, 12, and 15 as
acute, right, or obtuse. Justify your
answer.
c2
= a2
+ b2
Compare c2
and a2
+ b2
.
?
152
= 122
+ 92
Substitution
?
225 = 225 Simplify and compare.
Answer: Since c2
= a2
+ b2
, the triangle is right.

23. Example 8
Classify the triangle with lengths 10, 11, and 13 as
acute, right, or obtuse. Justify your answer.
c2
= a2
+ b2
Compare c2
and a2
+ b2
.
?
132
= 112
+ 102
Substitution
?
169 < 221 Simplify and compare.
Answer: Since c2
< a2
+ b2
, the triangle is acute.

24. Your Turn:
A. acute
B. obtuse
C. right
A. Classify the triangle with lengths 7, 8, and 14 as
acute, right, or obtuse.

25. Your Turn:
A. acute
B. obtuse
C. right
B. Classify the triangle with lengths 26, 22,
and 33 as acute, right, or obtuse.

26. Joke Time
• What is black, white and red all over? You fold it!
• A newspaper.
• How can you tell if there is an elephant in your fridge?
• You can't close the door.
• What did one wall say to the other?
• "I'll meet you in the corner."